멀티웨이 탐색 트리
개관
이진 탐색 트리를 발전시킨 멀티웨이 탐색 트리에 대해 알아본다. 이것은 기존 이진 탐색 트리의 장점을 활용하면서, 보다 다양한 형태의 자식 노드를 가질 수 있도록 확장한 개념이다.
- m원 탐색 트리:
- m개 이하의 가지를 가질 수 있는 확장된 형태의 탐색 트리.
- 이진 탐색 트리는 사실상 2-way 탐색 트리의 한 형태.
- 파일 인덱스 구현에 효율적으로 사용 가능하며, 빠른 레코드 참조가 장점.
- B, B*, B+ 트리:
- 이들 트리는 서로 다른 조건과 특징을 가지며, 각각의 삽입 및 삭제 방법을 이해하는 것이 중요.
- B 트리: 루트와 단말 노드를 제외한 모든 노드가 최소 (M/2)개의 서브트리를 가져야 함. 루트는 최소 2개의 서브트리를 보유. 모든 단말 노드는 같은 레벨에 위치.
- B* 트리: 노드가 약 2/3 이상 차야 하는 B 트리의 변형. 노드 분리 최소화를 위해 고안됨. 노드가 꽉 찼을 때 분리하지 않고 키와 포인터를 재배치하여 다른 형제 노드로 이동.
- B+ 트리: B 트리와 유사하나, 잎 노드가 모든 키값을 포함하고 이를 순차적으로 연결하는 포인터 집합이 존재하는 점에서 차이. 순차 처리 시 용이.
멀티웨이 탐색 트리는 이진 탐색 트리의 효율성을 유지하면서 다양한 형태의 데이터 구조 및 애플리케이션에 대응할 수 있는 유연성을 제공한다.
1. m원 탐색 트리
m원 탐색 트리는 이진 탐색 트리를 확장한 것이다. 이진 탐색 트리의 경우 2-way 탐색 트리이다. m원 탐색 트리는 탐색 트리의 제한을 따르되 두 개 이상의 자식을 가질 수 있게 되는 것이다. 정의는 다음과 같다.
1) 노드 구조는 다음과 같다. 여기서 p0, p1, ..., pn은 서브트리에 대한 포인터이고 k0, ..., kn-1은 키값이다. 또한 n<=m-1이 성립한다.
2) i=0, ..., n-2인 i에 대해 ki<ki+1을 만족한다.
3) i=0, ..., n-1인 i에 대해 pi가 가리키는 서브트리의 모든 키값은 ki의 키값보다 작다.
4) pn이 가리키는 서브트리의 모든 키값은 kn-1의 키값보다 크다.
5) i=0, ..., n인 i에 대해 pi가 가리키는 서브트리는 M원 탐색 트리이다.
다음 그림은 3원 탐색 트리를 나타낸다.
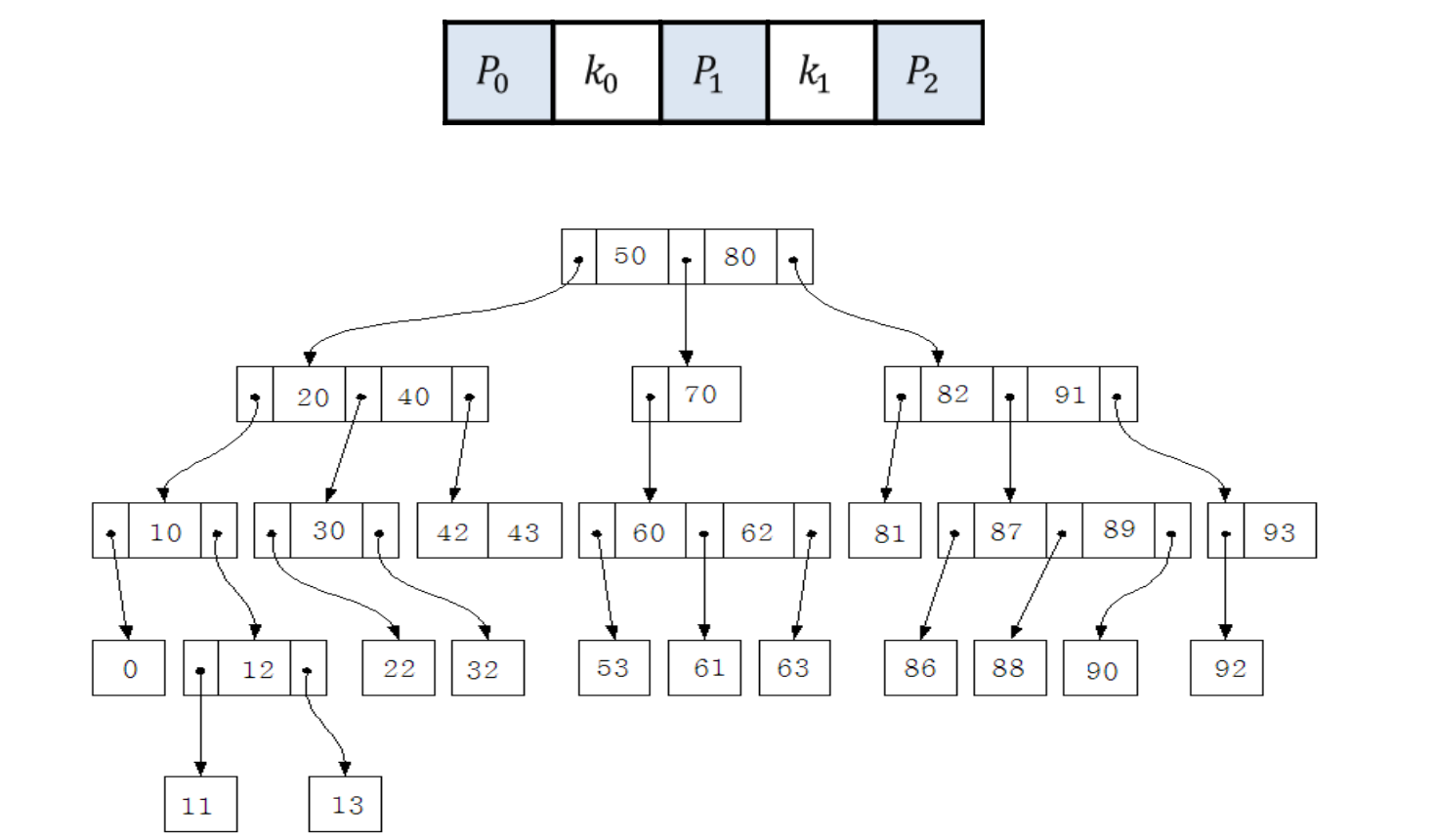
모든 노드가 딱 세개의 서브트리를 갖는 것이 아니라 최대 세 개까지 서브트리를 갖는 개념이다. 그리고 탐색 트리의 요건으로서, 왼쪽은 작고 오른쪽은 크다.
노드 구조는 다음과 같다.
struct Mnode{
int n;
struct rectype {
struct Mnode *ptr;
int key;
struct Rectype *addr;
} keyptrs[n-1];
struct Mnode *keyptrn;
}자바 코드
class Mnode {
int n;
Rectype[] keyptrs;
Mnode() {
keyptrs = new Rectype[n - 1];
}
class Rectype {
Mnode ptr;
int key;
Rectype addr;
}
Mnode keyptrn;
}
m원 트리를 위한 노드는 중첩 구조체로 정의한다. 즉, 구조체 안에 구조체가 또 들어 있다. 서브트리를 위한 포인터와 키값이 반복해서 나타나면서 m개 까지 서브트리를 갖게 된다.
변수 n은 무엇일까? 각 노드가 갖는 서브트리 개수는 제각각이다. 예를 들어 루트 노드는 세 개의 서브트리를 갖는다. 반면에 루트 가운데 서브트리는 서브트리를 하나만 갖는다. 그러므로 각 노드가 몇 개의 서브트리를 갖는지는 나타낼 필요가 있다. 그것을 저장하는 변수이다.
- 변수
n의 역할:n은 각 노드가 실제로 가지고 있는 서브트리의 개수를 나타낸다. 이는 각 노드마다 서브트리의 수가 다를 수 있기 때문에 중요하다. 예를 들어, 루트 노드는 3개의 서브트리를 가질 수 있지만, 그 중 하나의 서브트리는 오직 하나의 서브트리만을 가질 수 있다. 따라서,n은 각 노드의 동적인 특성을 반영하는 데 필요하다. Rectype중첩 클래스/구조체: 이 중첩 클래스/구조체는 각 노드의 서브트리 포인터(ptr), 키(key), 추가적인 주소 정보(addr)를 포함한다. 이는 m원 트리에서 각 노드가 여러 개의 서브트리와 관련 데이터를 관리할 수 있도록 해준다.keyptrs배열: 이 배열은Rectype객체들을 저장한다. 각Rectype객체는 트리의 각 서브트리와 그에 연결된 키 및 추가 정보를 담고 있다. 배열의 크기는n-1로 설정되어 있는데, 이는 노드가 가질 수 있는 최대 서브트리 수에 따라 동적으로 결정된다.keyptrn포인터/참조: 이는 마지막 서브트리를 가리키는 포인터 혹은 참조이다.keyptrs배열이n-1개의 서브트리를 처리하므로, 이 포인터는 마지막 서브트리를 처리한다.
키값을 찾는 과정은 이진 탐색 트리에서 키값을 찾는 과정을 확장하면 된다. m원 탐색 트리의 탐색 함수는 다음과 같다.
m원 탐색에서 키값을 찾는 연산
struct Mnode *nodeptr;
struct rectpye *recptr;
struct rectpye *Search(int skey, structMnode *r) {
int i;
extern struct Mnode node;
if (r == null) return null;
else {
i = 0;
while (i < r -> n && skey > r ->keyptrs[i].key) i ++;
if (i <r->n && skey == r -> keyptrs[i].key) return (r ->keyptrs[i].addr);
else if (i< r-> n) return (Search(skey, r->keyptrs[i].ptr));
else return (Search(skey, r->keyptrn));
}
} 자바 코드
class MTreeSearch {
Mnode nodeptr;
Rectype recptr;
public Rectype search(int skey, Mnode r) {
int i;
if (r == null) return null;
else {
i = 0;
while (i < r.n && skey > r.keyptrs[i].key) i++;
if (i < r.n && skey == r.keyptrs[i].key) return r.keyptrs[i].addr;
else if (i < r.n) return search(skey, r.keyptrs[i].ptr);
else return search(skey, r.keyptrn);
}
}
}
skey는 탐색을 위한 키값이고 r은 루트 노드를 가리키는 포인터이다. 해당 노드의 서브트리 개수 (R->n)만큼 반복하면서 키값을 비교하여 왼쪽, 가운데, 오른쪽으로 찾아 내려간다.
- 탐색 연산은 루트 노드부터 시작하여 각 노드의 키값들과 탐색 키
skey를 비교한다. while (i < r.n && skey > r.keyptrs[i].key) i++;반복문은 현재 노드의 키들을 순회한다. 탐색 키가 노드의 키보다 크면 다음 키로 이동한다.- 일치하는 키를 찾으면 (
if (i < r.n && skey == r.keyptrs[i].key)), 해당 키와 연결된 주소(r.keyptrs[i].addr)를 반환한다. - 현재 노드에서 일치하는 키를 찾지 못하면, 적절한 서브트리로 이동한다.
i < r.n이면 탐색 키가 노드의 일부 키보다 작다는 의미이므로 왼쪽 서브트리 중 하나로 이동(r.keyptrs[i].ptr)한다. 그렇지 않으면 가장 오른쪽 서브트리로 이동한다(r.keyptrn).
전반적으로, 노드당 자식 또는 서브트리의 수가 많을수록 최대 탐색 경로는 짧아지는 경향이 있다. 이는 노드 당 서브트리가 많을수록 트리의 깊이가 얕아져 탐색 속도가 빨라지기 때문이다. 예를 들어, 키가 255개인 경우 4원 트리로 구성하면 최대 경로 길이는 4가 되어 4번만에 탐색을 완료할 수 있다.
2. B 트리
노드의 가지 개수를 늘리는 것만이 m원 탐색 트리의 성능을 향상 시키는 것은 아니다. BS 트리에서처럼 트리의 균형을 유지하여야 성능을 개선할 수 있다. m원 탐색 트리에서도 전체적인 균형을 고려하면 성능이 향상된다.
다음 조건을 만족하는 m원 탐색 트리를 차수 M인 B트리라고 한다. 이 트리는 인덱스 구조를 구현할 때 일반적으로 사용되는 트리이다.
1) 루트와 잎 노드를 제외한 트리의 각 노드는 최소 [m/2]개의 서브 트리를 갖는다.
2) 트리의 루트는 최소한 두 개의 서브트리를 갖는다.
3) 트리의 모든 잎 노드는 같은 레벨에 있다.
조건 1은 트리의 각 내부노드가 최소한 반이 차 있어야 한다는 것을 뜻한다. 여기서 []는 가우스 함수인데 소수점을 포함하는 수를 그것보다 1 큰 정수로 바꾸는 함수다. 예를 들어 [3/2] = 1.5 => 2이다. 그러므로 3원 트리의 각 노드는 최소 2개의 서브트리를 갖도록 하는 것이다.
조건 2는 트리를 처음부터 분리되도록 한다. 루트부터 최소한 두 개의 서브트리를 갖도록 하는 것이다. 그리고 조건 3에 의해 트리가 거의 균형 잡히도록 한다. 즉, 내부를 충분히 채우고, 이 노드 중 자식을 갖지 않은 것이 있는 한 새로운 가지치기, 즉 높이를 증가시키는 일을 하지 않는 것이다.
차수 m인 B 트리의 탐색 경로 길이는 같은 개수의 키를 가지는 이상적인 m원 탐색 트리보다 길어질 수 있다. 하지만 B 트리를 유지하는 것이 이러한 이상적인 m원 트리를 유지하는 것보다 훨씬 쉽다. 결국 최적인 M원 탐색 트리보다 차수 m인 B 트리를 이용하는 이유는 완전히 균형잡힌 이진 탐색 트리보다 AVL 트리 또는 BB 트리를 이용하는 이유와 같다고 할 수 있다. 즉, 키값을 삽입이나 삭제할 때 드는 노력이 적기 때문이다.
그럼에도 최대 탐색 길이는 같은 차수를 갖는 균형 잡힌 m원 탐색 트리의 경우와 거의 비슷하므로 B 트리가 좋은 것이다.
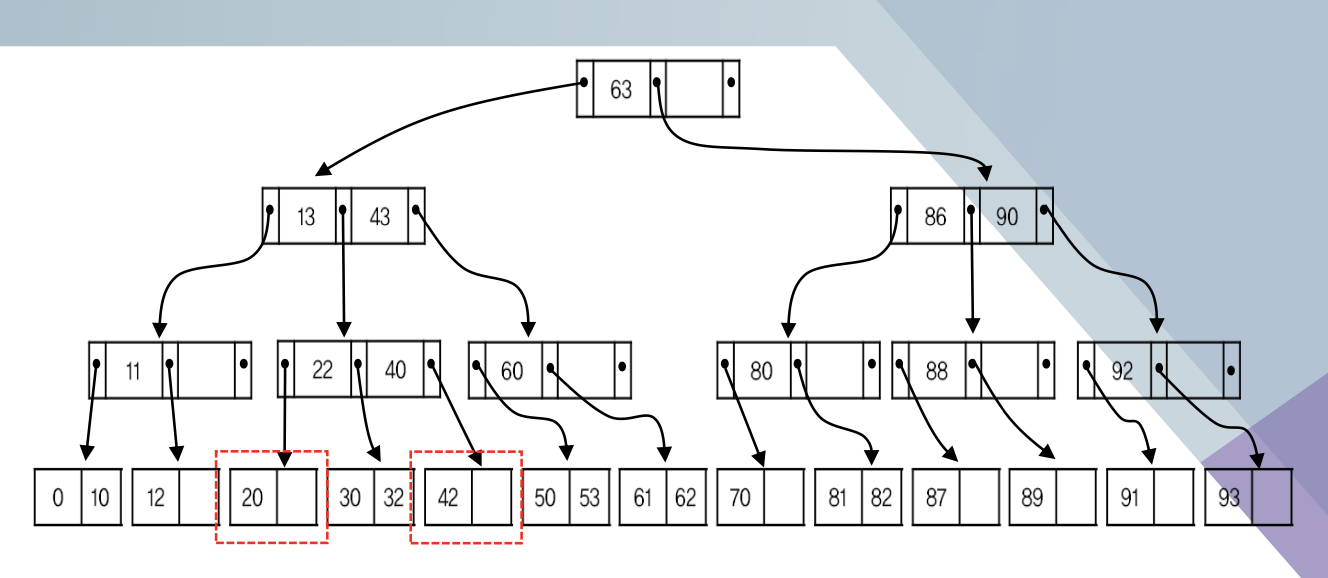
위의 그림을 다시 B 트리로 구성해보면 다음과 같다.

AVL 트리, BB 트리 및 Splay 트리 역시 균형 트리였는데 이들은 사실 2원 탐색 트리의 특수한 경우들이었다. 이 트리들의 경우 균형을 맞추기 위해 회전 연산을 사용했다. B 트리는 보다 간단한 방법으로 균형을 유지할 수 있다.
1) B 트리 노드 삽입
삽입 알고리즘은 다음과 같다.
1. 삽입할 위치를 찾기 위해 노드의 키값을 좌에서 우로 탐색ㅎ한다. (B 트리에서 모든 노드는 잎에서 삽입이 개시됨)
2. 노드에 빈자리가 있으면 삽입 후 종료한다.
3. 노드가 꽉 찼으면 노드를 두 개로 분리하고 키와 포인터를 새 노드에 반씩 할당한다.
3-1. 잎 노드 키값과 삽입 노드 키값 중에서 중간값을 선택한다.
3-2. 선택된 중간값보다 작은 키값을 갖는 것은 왼쪽 노드에 넣고 큰 것은 오른쪽 노드에 넣는다.
3-3. 중간값을 가지는 노드의 키와 포인터를 부모 노드에 삽입한다. 만일 부모 노드가 루트 노드이면 두 노드를 가리키도록 (자식 노드가 되도록) 수정한다.
노드가 꽉 차 있는 경우는 분리해서 키값과 포인터를 재분배해야 한다.
삽입 하는 예시를 살펴보자. 21의 경우 비어 있는 자리에 그냥 넣으면 된다. 42의 경우 키값의 순서를 유지하면서 넣으면 된다.
54와 60은 왼쪽에 놓여야 한다. 그런데 그 노드가 꽉찬 상황이다. 노드 분리가 필요하다.

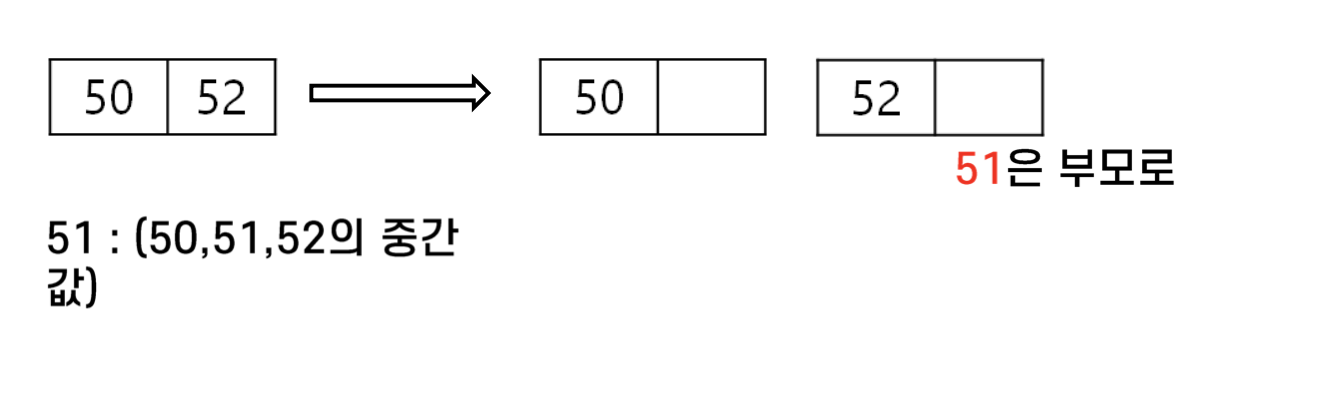
52는 다음과 같이 쉽게 삽입할 수 있다.

그렇다면 51은 어떠할까? 50과 52 사이에 넣어야 하기 때문에 먼저 노드를 분리해야 한다.
그런 뒤 중간값인 51을 부모로 보낸다. 여기서 문제가 생기는데, 부모노드가 꽉 차 있는 것이다. 앞 단계에서 53이 들어가며 자리를 차지했다. 따라서 부모노드를 분리해야 항ㄴ다. 분리하면 다음과 같다.

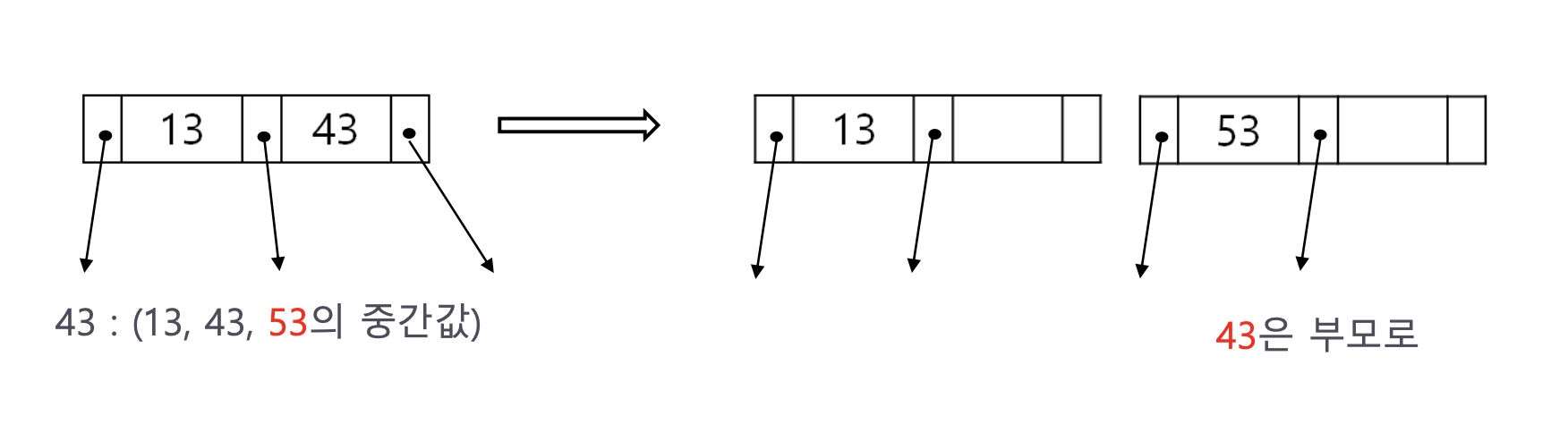
중간값 54을 부모 노드 어딘가에 저장해야 하는데 부모노드가 (13, 43)이 꽉찬 상황이다. 그러므로 이 노드 역시 분리 해야 하고, 키값 53 왼쪽 포인터가 키값 51노드를 가리키도록 수정하고 오른쪽 포인터는 키값 60인 노드를 가리키도록 수정한다.
이제 키값 43을 부모 노드에 넣는다.

결과적으로 다음과 같은 트리가 완성된다.

2) B 트리 노드 삭제
삭제의 경우 삽입보다 복잡하다. B 트리이기 위해서는 어떤 노드가 정해진 개수의 키를 가져야 해서 삭제 결과 개수가 부족하면 그 노드를 다른 노드와 묶어야 한다.
키 삭제 알고리즘은 다음과 같다.
삭제할 키 값을 포함한 노드를 찾는다.
- 잎 노드에서 삭제하는 경우
- 노드에서 키값을 삭제
- 필요하면 재배열
- 내부 노드에서 삭제하는 경우
- 내부 노드 키값은 하위 노드에 대한 기준값(중간값)이 없기 때문에 삭제 시 대체할 수 있는 적절한 값을 찾아야 한다. 보통 왼쪽 서브트리의 가장 큰 키값 또는 오른쪽 서브트리의 가장 작은 키값으로 대체할 수 있다. 이들은 모두 잎에 위치한다.
1. 새로운 기준값을 선택하여 해당 잎 노드에서 삭제하고 그 값을 현재 키값을 삭제한 자리로 옮긴다. 즉 대체한다.
2. 기준값으로 대체하기 위해 키를 삭젷한 잎 노드가 정해진 개수의 키값을 갖지 않으면 트리를 재배열 한다.
- 재배열
1. 키값이 부족한 노드의 오른쪽 형제가 존재하고 키가 정해진 개수보다 많다면 왼쪽으로 회전한다.
2. 키값이 부족한 노드의 왼쪽 ㅎ형제가 존재하고 키가 정해진 개수보다 많다면 오른쪽으로 회전한다.
3. 좌우 형제가 최소 개수의 키를 가지고 있다면 좌우 형제를 합친다.
62, 0, 40을 삭제하는 경우를 생각해보자.
62의 삭제는 잎에 있기 때문에 그냥 삭제하면 된다.
0을 삭제하는 경우 키 순서를 유지하기 위해 10을 왼쪽으로 이동한다.
40을 삭제하는 경우, 해당 노드는 잎 노드가 아니고 키값이 하나도 없다. 이 노드에 적당한 키를 끌어다 놓아야 한다. 삭제한 키 오른쪽 포인터가 가리키는 서브트리에서 가장 왼쪽 키를 가져온다.

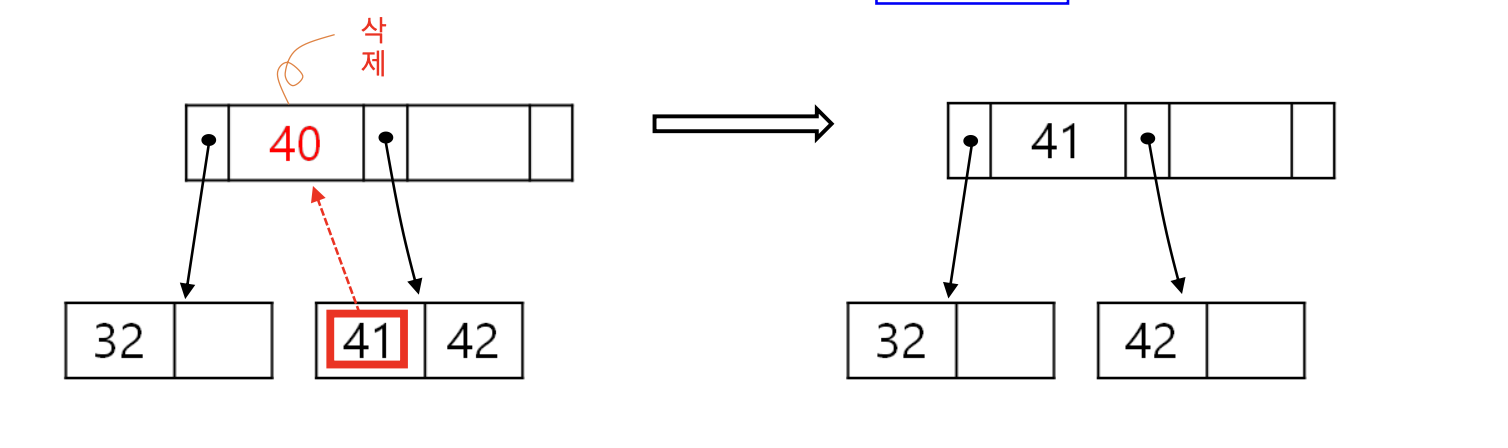
11을 삭제하는 경우는 어떨까? 다음과 같은 재결합이 필요하다.

3. B*, B+ 트리
1) B* 트리
노드의 약 2/3 이상이 차야하는 B트리를 B* 트리라고 한다.
B* 트리는 노드가 꽉차면 분리하지 않고, 키와 포인터를 재배치하여 다른 형제 노드로 옮긴다. 삽입, 삭제시 발생하는 노드 분리를 줄이려고 고안한 것이다.
1) 공집합이거나 높이가 1이상인 m원 탐색트리
2) 루트 노드는 2개 이상 2[(2m-2)/]+1 이하의 자식 노드를 갖는다.
3) 내부 노드는 최소한 [(2ㅡ-1)/3]개의 자식 노드를 갖는다.
4) 모든 잎 노드는 동일한 레벨에 놓인다.
5) 포인터가 k개인 잎 노드가 아닌 노드는 k-1개의 키를 갖는다
B* 트리에 노드를 삽입하는 과정은 다음과 같다.
5원 탐색 트리에 4를 삽입해보려고 하는데 왼쪽 자식 노드에 빈자리가 없는 경우이다.

B* 트리는 분리를 하는 대신 형제 노드로 키값을 이동한다. 전체 키 개수의 절반(1,2,3)은 왼쪽 서브 노드에 넣고, 중간 키값은 (4) 부모 노드에 기준값으로 배치하고, 나머지 절반은 오른쪽 서브 노드에 배치한다.

만약 오른쪽 서브 노드, 즉 형제 역시 차 있는 경우 B* 트리에서는 두 개의 노드를 세 개의 노드로 분리한다. 그렇다면 결과적으로 각 노드는 약 2/3가 차게 된다.

이 상태에서 키값 4를 삽입하려는 경우 왼쪽 서브 노드에 넣어야 하는데 자리가 없다. 따라서 두 노드를 세 개로 분리하여 각 노드의 약 2/3가 차도록 만든다.
B 트리의 내부 노드는 약 반이 차지만, B* 트리는 약 2/3가 찬다는 점에서 다르다. 따라서 동일한 노드의 수를 갖는 경우 B* 트리는 B 트리보다 높이가 낮을 확률니 높고 따라서 탐색 시간 성능이 향상된다. 또한 키 삽입시 B* 트리는 B 트리보다 분리 횟수가 작다는 장점도 있다.
B* 트리와 B 트리 비교: 장단점
B* 트리와 B 트리는 비슷한 구조를 가지고 있지만, 몇 가지 중요한 차이점이 있다. 이러한 차이점으로 인해 각각의 트리는 고유의 장단점을 갖는다.
B* 트리의 특징 및 장점:
- 노드의 채움도가 높다: B* 트리의 각 노드는 약 2/3 이상 채워져 있어야 한다. 이는 B 트리의 약 1/2 채움도에 비해 높은 효율성을 의미한다.
- 트리 높이가 낮을 가능성이 높다: 노드가 더 많이 채워져 있기 때문에 같은 수의 노드를 가진 B* 트리는 B 트리보다 높이가 낮을 가능성이 높다. 이는 탐색 시간을 단축시킨다.
- 노드 분리 횟수 감소: B* 트리는 노드가 꽉 찼을 때 바로 분리하지 않고, 키와 포인터를 재배치하여 형제 노드로 이동시킨다. 이는 노드 분리가 덜 자주 일어나게 함으로써 노드 분리로 인한 비용을 줄인다.
B 트리의 특징 및 장점:
- 단순한 구조: B 트리는 노드가 최소 1/2 정도만 채워져 있으면 되므로 구현이 비교적 단순하다.
- 유연한 노드 관리: 노드 분리와 합병이 상대적으로 더 자주 일어날 수 있으므로, 다양한 상황에 대응하기 쉽다.
2) B+ 트리
단순 연결 리스트는 저장된 데이터를 차례로 처리하는 데 적합하다. 헤드부터 링크를 쫓아가며 다음 노드들을 차례로 처리하기 때문이다. 그러나 특정 값을 탐색하는 경우에는 적절하지 않다.
마찬가지로 탐색 트리에서도 데이터를 매번 왼쪽 오른쪽 비교하며 처리면서 불편함이 있다. B+ 트리는 인덱스된 순차 파일을 구성하는데 사용되는데, 인덱스된 순차 파일은 데이터를 차례로 순차 처리와 특정 데이터를 직접 찾아 처리하는 두 가지를 모두 효율적으로 가능하게 하는 구조이다.
B+ 트리는 B 트리와 같이 각 노드의 키값이 적어도 1/2이 차야한다는 점은 동일하다. 하지만 잎 노드를 순차적으로 연결하는 포인터 집합이 있다는 점에서 다르다. B+ 트리는 잎 노드의 마지막 포인터를 다음 키값을 갖는 노드를 가리킨다. 따라서 순차처리를 할 때 이 포인터를 이용하여 차례로 다음 데이터에 접근한다.

요약
- 트리의 노드가 m개 이하의 가지를 가질 수 있는 탐색 트리를 m원 탐색 트리라고 한다.
- M원 탐색 트리는 이진 탐색 트리를 확장한 것으로 탐색 트리의 제한을 따르되 두 개 이상 (m개 이하) 자식을 가질 수 있다.
- 인덱스 구조를 궇현하는 데 가장 일반적으로 사용하는 것으로 차수가 M인 B 트리가 있다.
- B 트리는 루트와 단말 노드를 제외한 트리의 각 노드가 최소 [M/2] 개의 서브트리를 갖는다.
- B 트리의 루트는 최소한 두 개의 서브트리를 갖는다.
- B 트리의 모든 단말 노드는 같은 레벨에 있다.
- B 트리의 삽입 연산에서 노드가 꽉 차 있는 경우는 분리해서 키값과 포인터를 재분배해야 한다.
- B 트리 삭제 연산에서 삭제 결과 개수가 부족하면 그 노드를 다른 노드와 묶어야 한다.
- 노드의 약 2/3 이상이 차야하는 B 트리를 B* 트리라고 한다.
- B* 트리는 노드가 꽉 차면 분리하지 않고, 키와 포인터를 재배치하여 다른 형제 노드로 옮긴다.
- B+ 트리는 인덱스는 순차 파일을 구성하는 데 사용한다. 인덱스는 순차 파일은 데이터를 차례로 처리하는 순차 처리와 특정 데이터를 직접 찾아 처리하는 두 가지를 모두 효율적으로 할 수 있는 구조이다.
- B+ 트리는 잎의 마지막 포인터가 다음 키값을 갖는 노드를 가리킨다. 따라서 순차 처리를 할 때는 이 포인터를 이용하여 차례로 다음 데이터에 접근해서 처리할 수 있다.
- B+ 트리에서는 모든 키값이 잎에 있고, 그 키값에 대응하는 실제 데이터에 대한 주소를 잎 노드만이 가지고 있다.
참고 자료: 자료구조 (강태원, 정광식 공저, KNOU press 출판)
'CS > 자료구조' 카테고리의 다른 글
| 자료구조 문제 풀이 (0) | 2023.11.26 |
|---|---|
| 멀티웨이 탐색 트리 2 : 2-3 트리, 2-3-4 트리, 레드 블랙 트리 (1) | 2023.11.26 |
| 이진 탐색 트리Bs) - Splay, Avl, BB 트리 (1) | 2023.11.25 |
| 선택 트리, 숲, 이진 트리 개수 (2) | 2023.11.25 |
| 힙 - 개념, 우선순위 큐, 삭제 삽입 연산 (1) | 2023.11.24 |


