개관
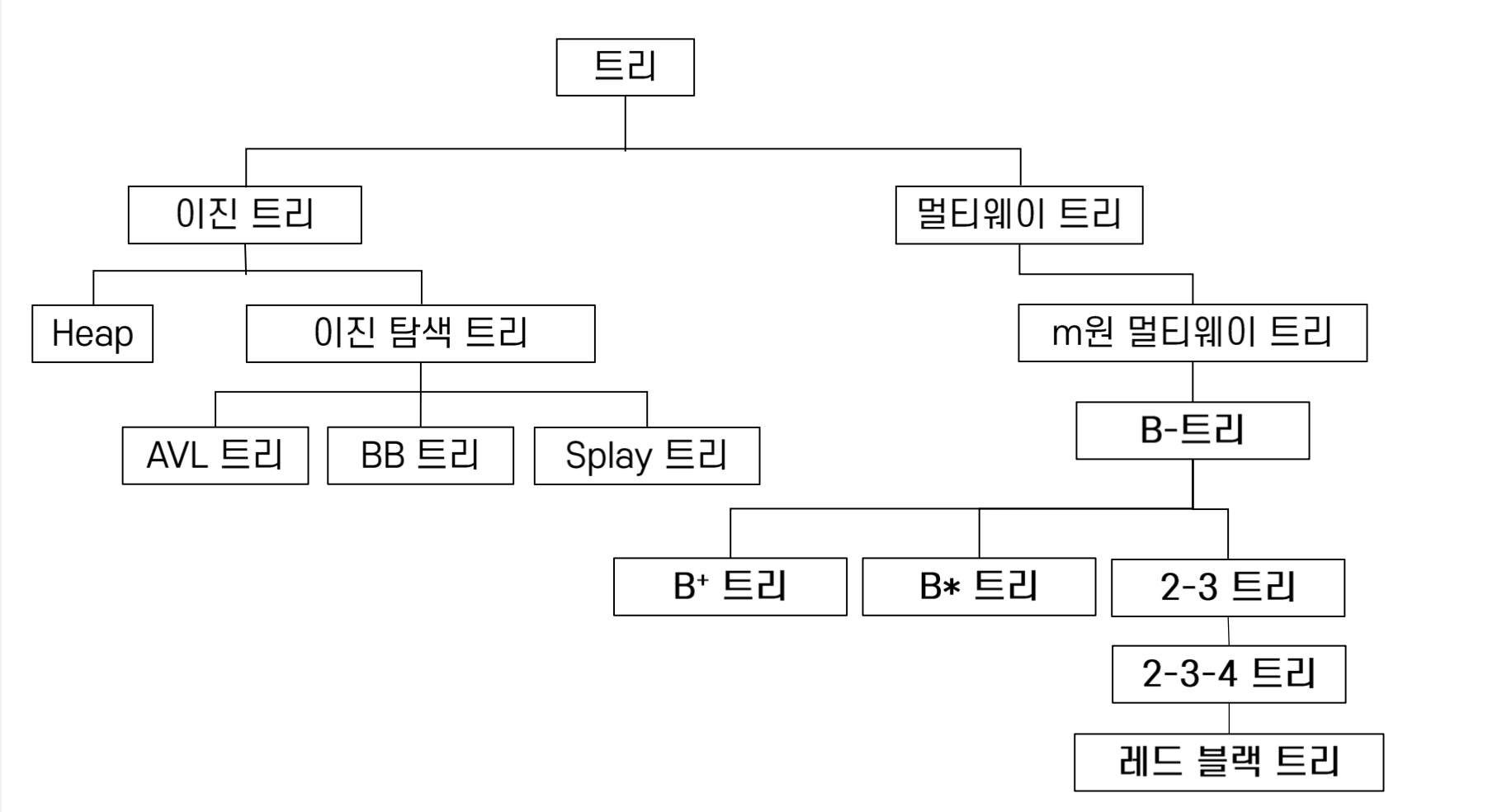
트리 구성도
1. 2-3 트리
차수가 2 또는 3인 내부 노드를 갖는 트리를 2-3 트리라고 한다. 이때 차수가 2인 노드를 2-노드, 3인 노드를 3-노드 라고 부른다. 즉, 2-3 트리는 2-노드와 3-노드만으로 구성된 특수한 형태의 B트리이다.
다음 조건을 만족할 때 2-3트리라고 한다.
1) 각각의 내부 노드는 2-노드 이거나 3-노드이다. 2-노드는 한 개의 키값을, 3-노드는 두 개의 키값을 갖는다.
2) lchild, mchild를 각각 2-노드의 좌측 및 중간 자식이라 하고, lkey가 이 노드의 키값이라 하면, 루트가 lchild인 모든 2-3 서브트리 키값은 lkey보다 작고, 루트가 mchild인 모든 2-3 서브트리 키값은 lkey보다 크다.
3) lchild, mchild 및 rchild를 각각 3-노드의 왼쪽, 중간 및 오른쪽 자식이라 하고, lkey 및 rkey를 이 노드의 두 키값이라 하자. 그러면 다음이 성립한다.
1) lkey < rkey
2) 루트가 lchild인 모든 2-3 서브트리 키값은 lkey보다 작다.
3) 루트가 mchild인 모든 2-3 서브트리 키값은 rkey보다 작고, lkey보다 크다.
4) 루트가 rchild인 모든 2-3 서브트리 데이터는 rkey보다 크다.
4) 모든 잎 노드는 같은 레벨에 있다.
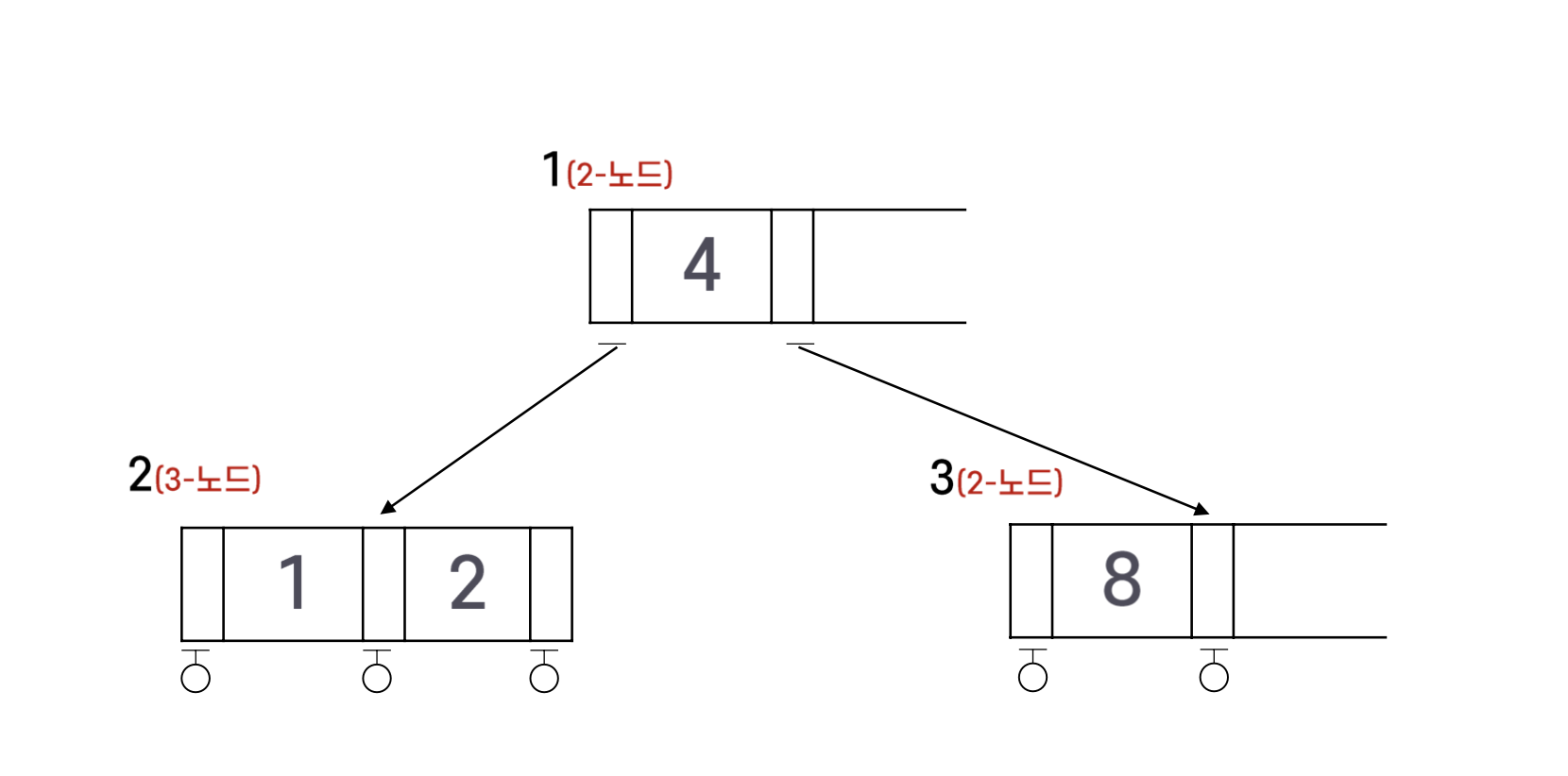
다음 그림은 2-3 트리를 보여준다. 노드 1과 3은 2-노드이고, 노드 2가 3-노드이다. 즉, 이 트리는 2-노드 2개와 3-노드 1개로 구성된 것이다. 포인터로 연결된 것 중에서 작은 원으로 표시한 것은 잎노드이다.
1) 2-3 트리의 탐색
2-3 트리에서의 탐색은 다음과 같은 이진 트리 탐색 알고리즘을 확장하여 구현할 수 있다.
typedef struct two_three *two_three_ptr;
struct two_three{
int lkey, int rkey;
two_three_ptr lchild, mchild, rchild;
};
two_three_ptr search23(two_three_ptr, t, int x) {
while (t)
switch(compare(x,t)) {
case 1: t= t->lchild;
break;
case 2: t= t->mchild;
break;
case 3: t= t->rchild;
break;
case 4: return (t) ;
}
return null;
}
2-3 트리 노드의 데이터 구조를 보면 포인터를 세 개까지 가질 수 있음을 알 수 있다.
그리고 탐색 함수 search23()에서 함수 compare(x,t)는 검색 키 x와 노드 t의 키값을 비교하는 함수이다. 노드 t에는 최대 두 개의 키값이 저장되어 있는데 complare(x,t)는 x가 이들 중 어느 것과 같은 경우, 왼쪽 키값보다 작은 경우, 왼쪽 키값보다 크고 오른쪽 키 값보다 작은 경우, 오른쪽 키값보다 큰 경우 등에 따라 각각 4, 1, 2, 3 값을 반환한다.
- 노드 구조 이해하기: 2-3 트리의 각 노드는 최대 2개의 키를 가질 수 있고, 이에 따라 최대 3개의 자식 노드(왼쪽, 중간, 오른쪽)를 가질 수 있다. 이 구조는 노드가 하나의 키를 가지고 있으면 2-노드, 두 개의 키를 가지고 있으면 3-노드라고 불린다.
- 탐색 키와 노드 키 비교하기: 탐색을 시작할 때, 우리는 먼저 탐색 키를 현재 노드의 키와 비교한다. 이때, 가능한 경우의 수는 총 4가지이다:
- 탐색 키가 현재 노드의 왼쪽 키보다 작다면 왼쪽 자식 노드로 이동.
- 탐색 키가 현재 노드의 왼쪽 키와 같다면 찾았으므로 탐색을 종료.
- 탐색 키가 왼쪽 키보다 크고 오른쪽 키보다 작다면 중간 자식 노드로 이동.
- 탐색 키가 현재 노드의 오른쪽 키보다 크다면 오른쪽 자식 노드로 이동.
- 재귀적으로 탐색하기: 위의 단계를 현재 노드에서 찾을 때까지 또는 트리의 끝에 도달할 때까지 반복한다. 이 과정에서 각 단계에서 올바른 자식 노드로 이동함으로써 효율적으로 탐색 키를 찾을 수 있다.
- 탐색 종료: 만약 탐색 키를 찾으면 해당 노드를 반환하고, 트리 끝에 도달하면 null을 반환하여 탐색이 실패했음을 나타낸다.
2) 2-3 트리의 삽입 및 삭제
다음과 같은 트리에 키값 7을 삽입하는 경우를 살펴보자.
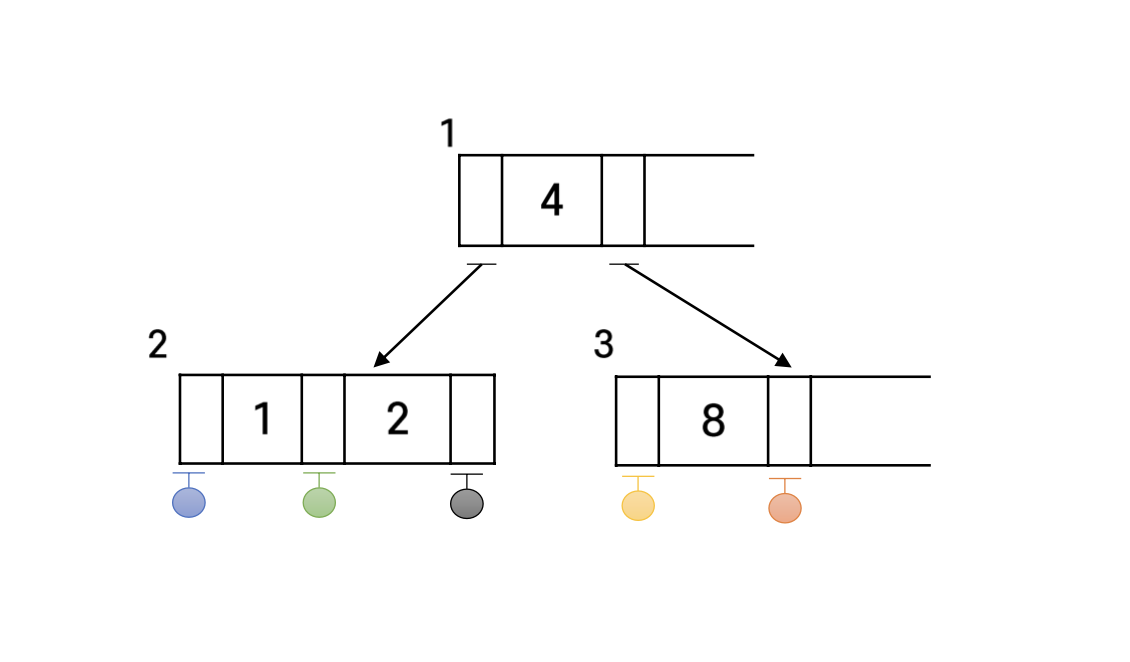
먼저 7이 트리에 없음을 확인된다면, 노드 3은 하나의 키값만 가지고 있으므로 이 노드에 다음과 같이 삽입한다.

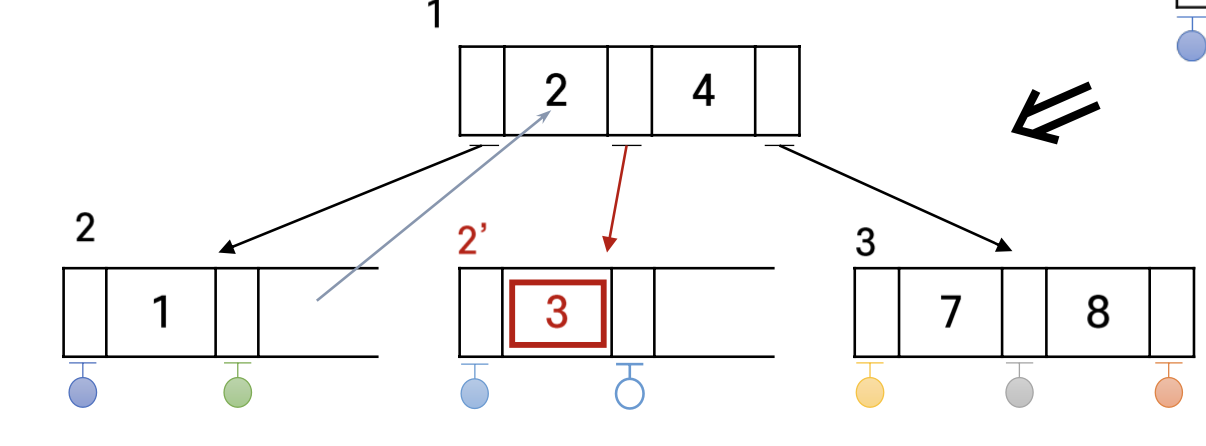
3이 삽입되는 경우는 어떨까? 노드 2에서부터 삽입이 시작된다고 하면, 자리가 없으므로 마련해야 한다. 이 새 노드를 2' 라고 하자. 2에는 현재 노드 2의 키값들 1,2와 삽입할 키값 3 중에서 가장 큰것이 들어가고 각 드는 키 1개씩을 갖도록 수정한다.
트리 삽입 알고리즘은 다음과 같다.
void insert23(two_three_ptr t, int y){
two_three_ptr q, p, r;
if (!(*)) new_root(t, y, null);
else { p=find_node(*t, y);
if (!p) {
fprintf(stderr, "the key is currently in the tree");
exit(1);
}
q = null;
for(;;)
if (p -> rkey == INT_MAX){
put_in(&p, y, q);
break;
}
else {
split(p, &y, &q);
if (p == *t) {
new_root(t, y, q);
break;
} else
p = delete();
}
}
}- 트리가 비어있는지 확인하기: 먼저, 트리가 비어있는지 확인. 트리가 비어있다면 새로운 키를 가진 루트 노드를 생성.
- 적절한 노드 찾기: 트리가 비어있지 않다면, 삽입할 키에 대한 위치를 찾기 위해 탐색을 시작. 이 과정에서 이미 트리에 동일한 키가 있는지도 확인.
- 노드에 여유 공간이 있는지 확인: 삽입할 위치를 찾았다면, 해당 노드에 여유 공간이 있는지 확인. 여유 공간이 있다면 간단하게 키를 삽입.
- 노드 분할하기: 여유 공간이 없다면 노드를 분할해야 한다. 이는 새로운 키를 포함하여 노드의 키를 정렬하고 중간값을 선택하여 두 개의 새로운 노드로 분할하는 과정을 포함한다.
- 부모 노드 업데이트: 분할된 두 노드는 부모 노드에 연결되어야 한다. 이때 부모 노드에도 여유 공간이 없다면 부모 노드도 분할해야 할 수 있다. 이 과정은 루트 노드에 도달할 때까지 계속될 수 있다.
- 새 루트 노드 생성: 만약 루트 노드까지 분할이 이루어진다면, 새로운 루트 노드가 생성되어야 한다.
2-3 트리의 삭제도 살펴보자.
잎이 아닌 노드의 키를 삭제하면 적당한 다른 키로 대체해야 한다.
다음과 같은 2-3 트리가 있다고 할 때 여기서 9를 삭제하면 다음과 같다.


7을 삭제해보자. 당사자인 노드 3이 공백이된다. 이때 회전하여 연산을 실행한다.
3-노드인 형제가 있는 경우 키값 중 하나를 부모로 올리고 대신 부모로부터 키값 하나를 가져다 빈 노드를 채운다.
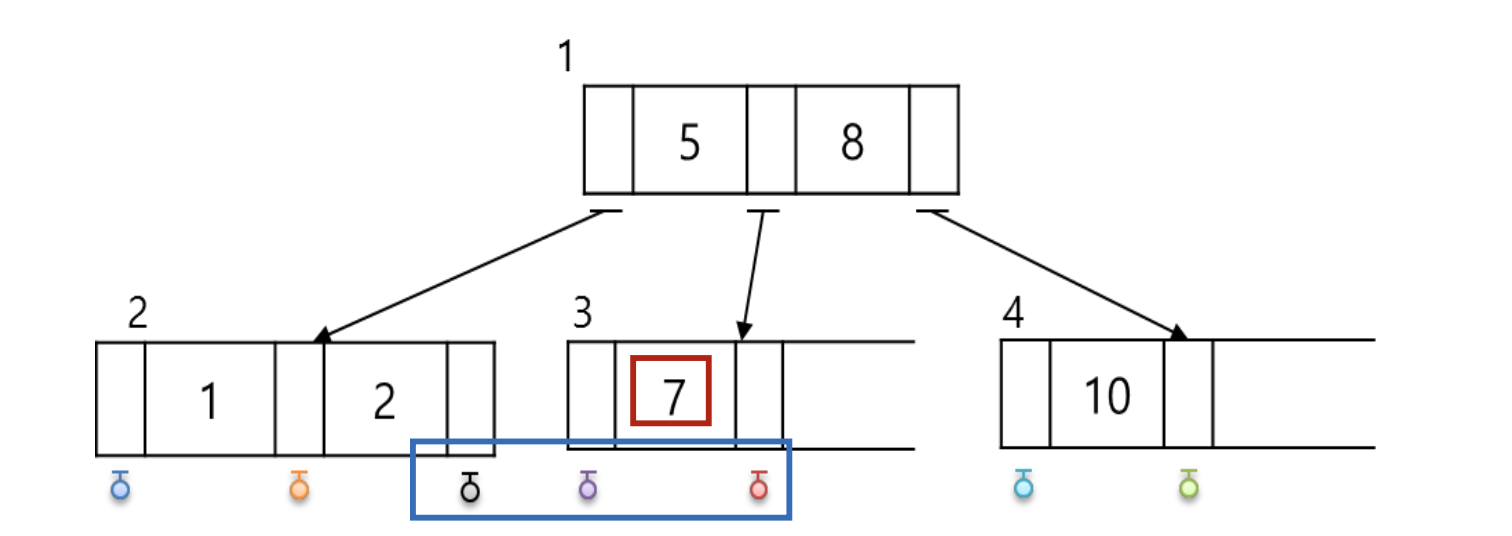

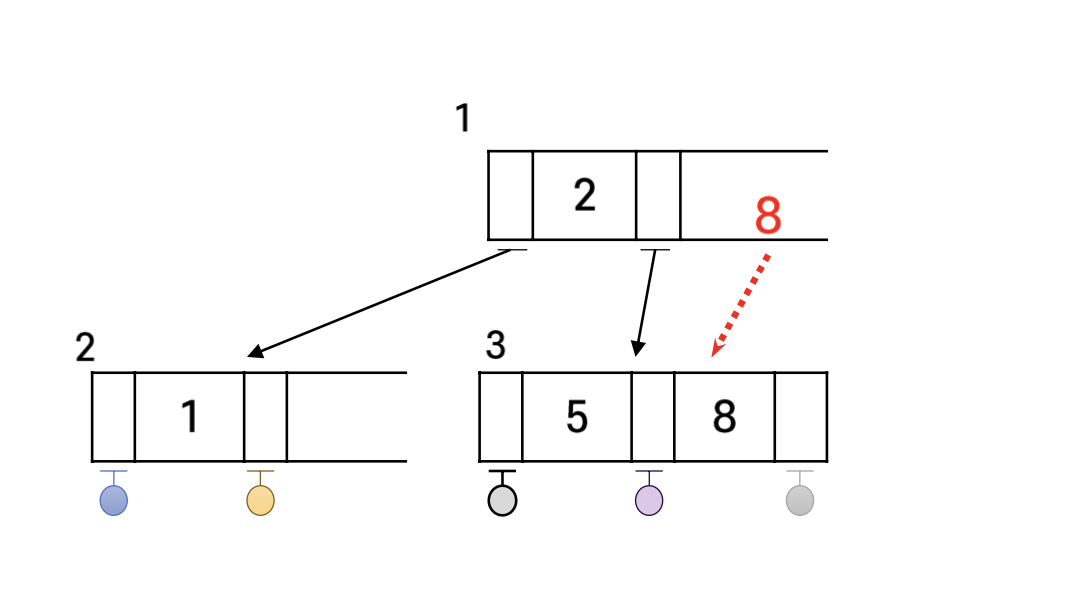
10을 삭제해 보자.
마찬가지로 노드 4가 공백이 된다. 이때 회전을 하려고 하니 3-노드인 형제가 없다. 따라서 이때는 결합 연산을 한다. 하나를 없애고 형제와 합친다.
2. 2-3-4 트리
- 노드의 종류: 내부 노드는 2-노드, 3-노드, 또는 4-노드가 될 수 있다.
- 2-노드: 하나의 키와 두 개의 자식을 가진다.
- 3-노드: 두 개의 키와 세 개의 자식을 가진다.
- 4-노드: 세 개의 키와 네 개의 자식을 가진다.
- 트리의 성질: 모든 잎 노드는 같은 깊이에 위치한다. 이는 트리가 완전히 균형을 이루고 있음을 의미한다.
- 탐색 방법: 이진 탐색 트리와 유사하게, 각 노드에서 키 값에 따라 탐색 경로를 결정한다. 예를 들어, 탐색 키가 노드의 키보다 작으면 왼쪽 자식으로, 크면 오른쪽 자식으로 이동한다.
- 삽입과 삭제: 2-3-4 트리는 삽입이나 삭제 시 노드의 분할 또는 결합을 통해 트리의 균형을 유지한다. 삽입이나 삭제 연산은 노드의 타입에 따라 달라지며, 트리의 깊이가 일정하게 유지되도록 조정한다.
2-3-4 트리 예시는 다음과 같다.
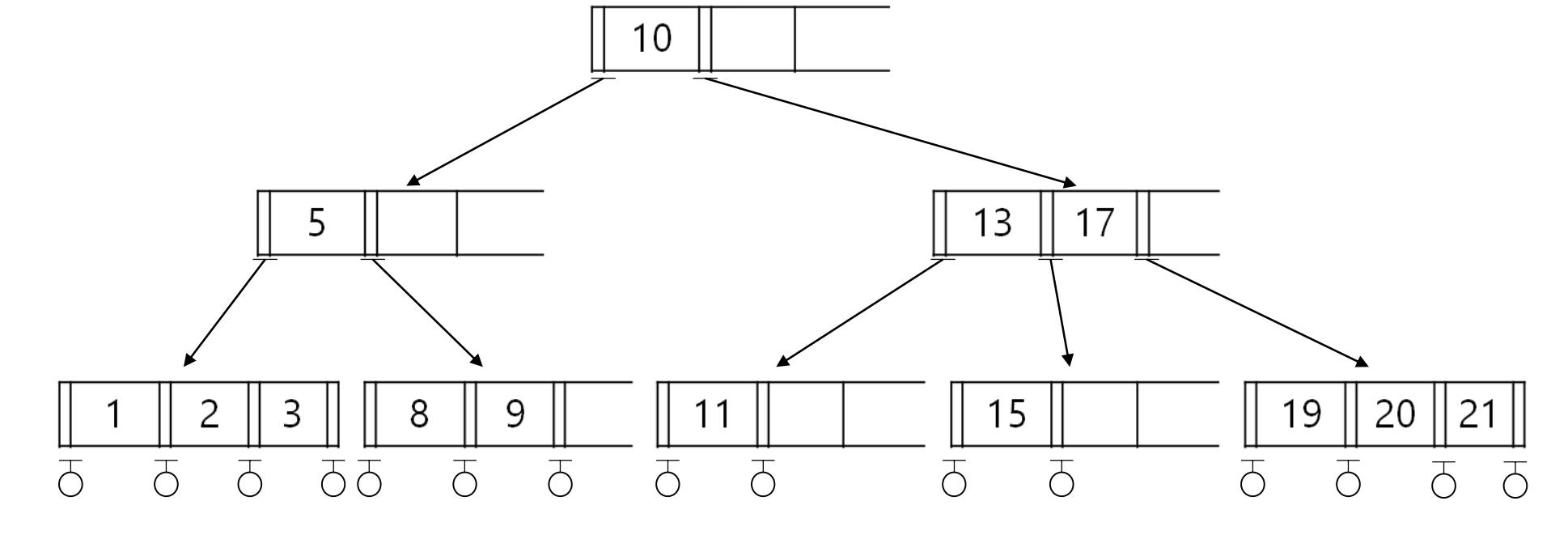
2-3-4 트리는 2-3 트리보다 삽입과 삭제가 용이하다.
2-3 트리에서는 각 연산에 대해 루트 노드에서 단말 노드로의 탐색 후에 다시 단말 노드에서 루트 노드 순으로 트리를 재구성하는 일이 자주 발생한다. 왜 그럴까? 아무래도 노드의 차수가 작기 때문이다. 그래서 삽입의 경우 분리 연산이 필요하고, 삭제의 경우 결합 연산이 필요하다.
반면 2-3-4 트리에서는 2-노드와 3-노드에 대한 트리 재구성의 확률이 2-3 트리보다 작아진다.
그러나 4-노드 의 경우 삽입 연산에서 동일한 재구성 과정이 필요하다. 다음 3가지 경우로 구분한다.
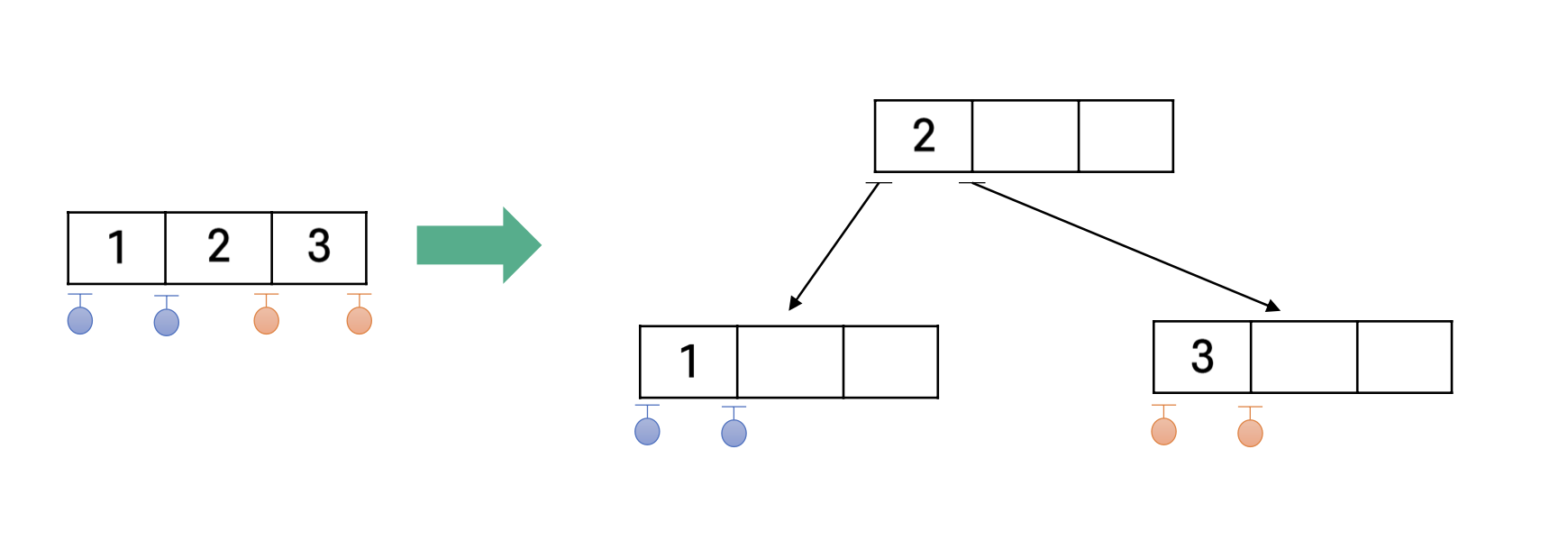
1) 4-노드가 2-3-4 트리의 루트인 경우
2) 4-노드의 부모다 2-노드인 경우
3) 4-노드의 부모가 3-노드인 경우
각각의 경우 다음과 같은 그림으로 살펴보자.
4-노드가 2-3-4 트리의 루트인 경우
4-노드의 부모가 2-노드인 경우
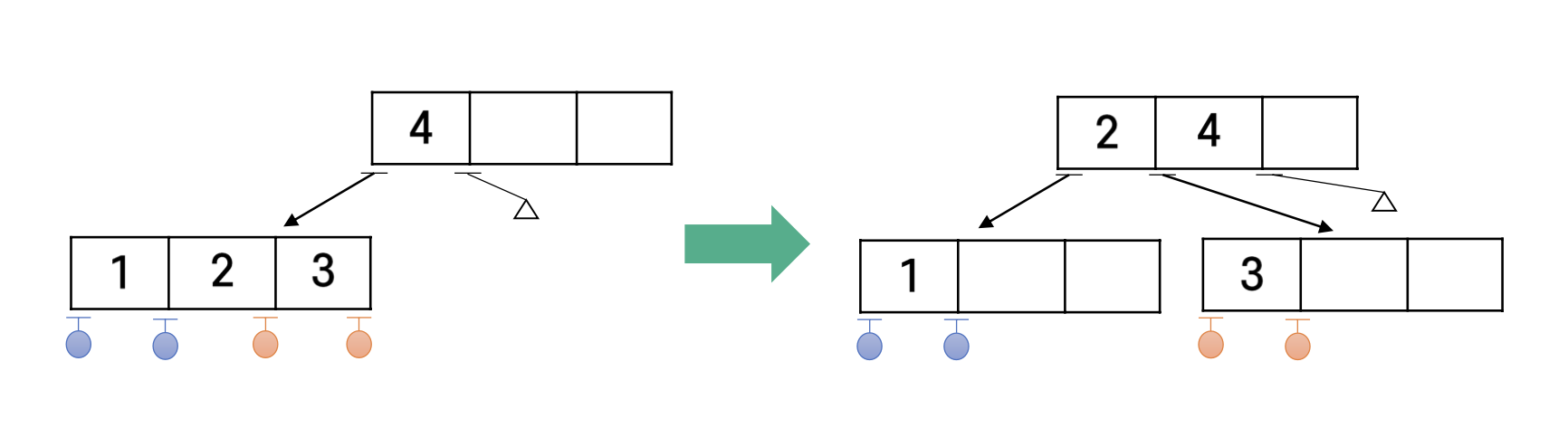
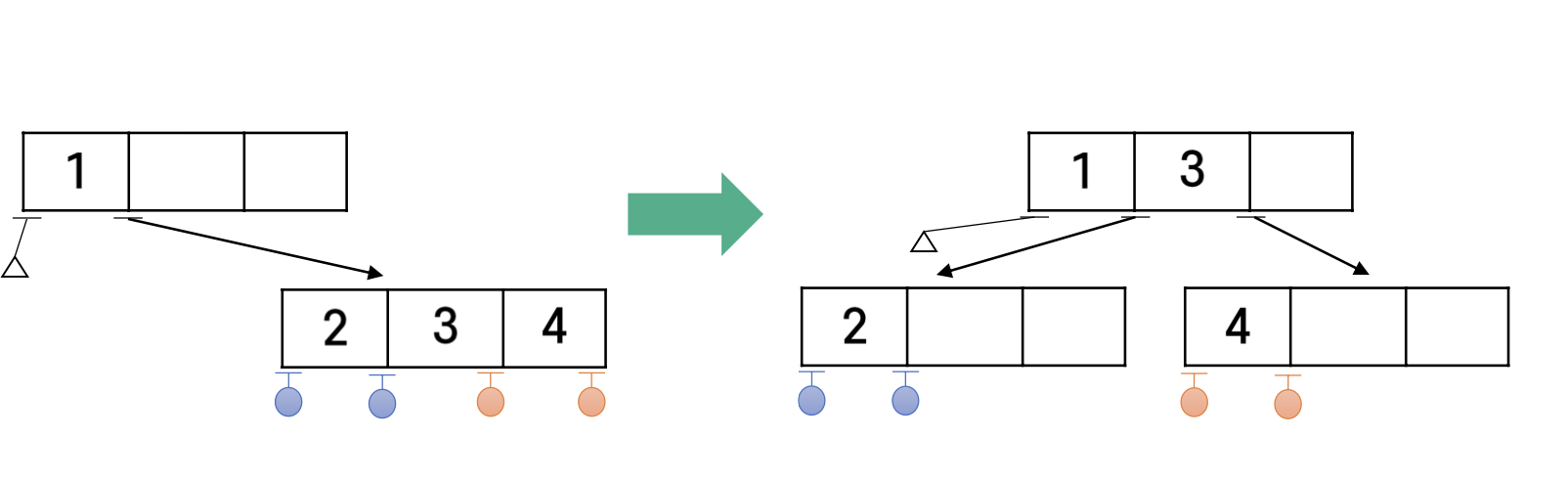
4-노드의 부모가 3-노드인 경우
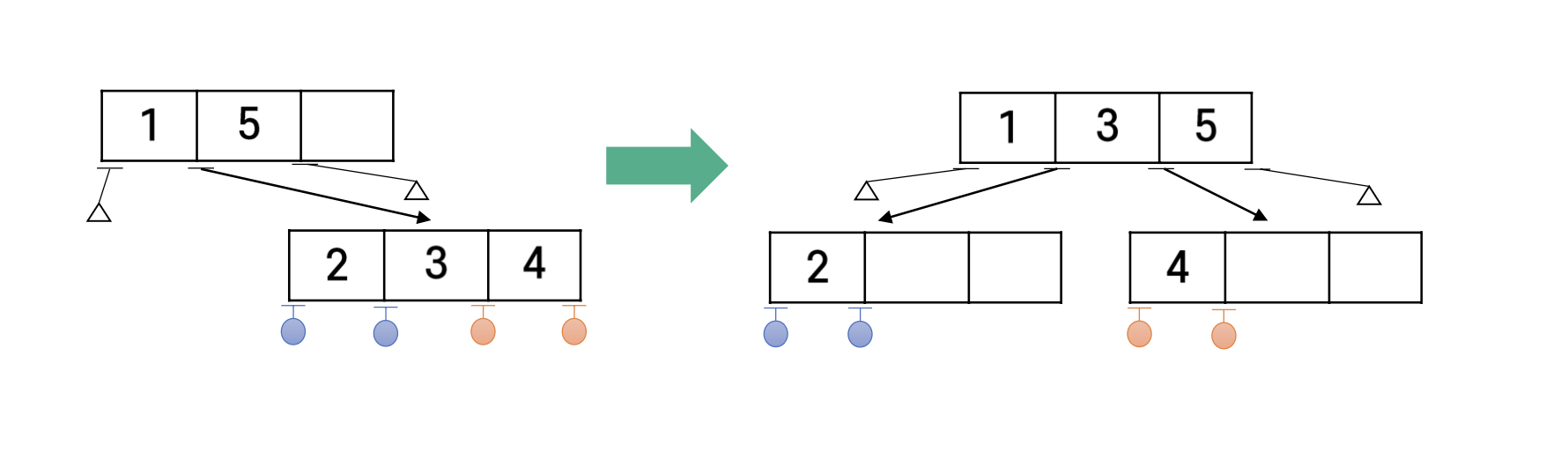
삭제의 경우도 3가지 케이스로 나누어서, 루트가 4-노드인 경우, 4-노드가 2-노드의 자식인 경우, 4-노드가 3-노드의 자식인 경우로 나누어서 연산할 수 있다.
3. 레드 블랙 트리
레드블랙 트리는 필요에 따라 효율적인 기억장소 사용을 위해 2-3-4 트리를 이진 트리로 나타낸 것이다.
레드블랙 트리에는 두 종류의 서브트리 포인터가 있는데, 하나는 레드 간선, 다른 하나는 블랙 간선이라고 한다. 레드 간선은 2-3-4 트리의 한 노드 내에 있던 항목이고, 블랙 간선은 2-3-4 트리의 포인터이다.

요약
- 차수가 2인 노드를 2-노드, 3인 노드를 3-노드라고 한다.
- 2-노드와 3-노드만으로 구성한 트리를 2-3 트리라고 한다. 이 트리는 균형이 잡힌 B 트리 계열과 거의 같은 성능을 유지하면서도 상대적으로 삽입과 삭제가 용이하다.
- 2-노드, 3-노드 및 4-노드만으로 구성한 트리를 2-3-4 트리라고 한다. 이 트리는 2-3 트리와 같은 특성을 갖는다. 대신 같은 수의 노드를 더 낮은 레벨로 구축할 수 있다.
- 2-3-4 트리는 4노드를 갖기 때문에 경우에 따라서는 기억 장소를 낭비할 수 있다. 기억 장소를 효율적으로 사용하기 위해 2-3-4 트리를 이진 트리롤 나타낸 것이 레드 블랙 트리이다.
참고 자료: 자료구조 (강태원, 정광식 공저, KNOU press 출판)
'CS > 자료구조' 카테고리의 다른 글
| 자료구조 슈도 코드 및 개념 요약 정리 : 배열, 스택, 큐, 연결 리스트, 이중 연결 리스트, 원형 연결 리스트 (0) | 2023.12.02 |
|---|---|
| 자료구조 문제 풀이 (0) | 2023.11.26 |
| 멀티웨이 탐색 트리 1 - m원 탐색 트리, B 트리, B*트리, B+ 트리 (2) | 2023.11.26 |
| 이진 탐색 트리Bs) - Splay, Avl, BB 트리 (1) | 2023.11.25 |
| 선택 트리, 숲, 이진 트리 개수 (2) | 2023.11.25 |

