힙
개요
힙은 부분적으로 정렬된 완전 이진 트리이며, 부모 노드와 자식 노드 간의 크기 관계를 통해 정의된다. 이러한 힙의 특성은 두 가지 주요 형태인 최대힙과 최소힙에서 나타난다. 최대힙에서는 부모 노드가 자식 노드보다 크며, 최소힙에서는 그 반대의 관계를 갖는다. 힙은 노드의 삽입 및 삭제 연산 시에 완전 이진 트리의 형태를 유지해야 하며, 이를 위해 노드 간의 관계를 조정한다.

*피라미드 모양으로 쌓아올린 더미를 힙이라고 한다.
우선순위 큐
우선순위 큐는 데이터가 우선순위에 따라 처리되는 자료 구조이다. 이 구조에서는 가장 높은 우선순위를 갖는 데이터가 먼저 나오는 것이 특징이다. 일반적인 큐와는 달리, 우선순위에 따라 데이터의 순서가 결정된다.
- 정의 및 특징: 우선순위 큐는 각 요소가 우선순위를 가지며, 우선순위가 높은 요소가 먼저 처리된다. 이는 일반 큐가 선입선출(FIFO) 원칙을 따르는 것과 대비된다.
- 사용 사례: 우선순위 큐는 CPU 스케줄링, 네트워크 트래픽 관리, 운영체제에서의 작업 관리 등 다양한 분야에서 사용된다.
예를 들어, 버스 정류장에서 줄을 서 있는 사람들이 있을 때, 일반적인 큐는 순서대로 버스에 탑승한다. 하지만 우선순위 큐에서는 특정 상황(예: 노약자, 임산부 등)에 따라 순서가 바뀔 수 있다.
배열을 이용한 우선순위 큐 구현
우선순위 큐를 배열로 구현할 때, 특정 규칙에 따라 데이터를 배열에 저장하고, 우선순위에 따라 데이터를 처리한다. 이 과정에서 배열의 인덱스가 중요한 역할을 한다.
- 데이터 삽입: 새로운 데이터를 배열의 마지막 위치에 추가한다. 이후, 부모 노드와 비교하여 우선순위에 따라 위치를 조정한다.
- 예시: 삽입 연산
Add_q(3)을 수행할 때, 3을 배열의 마지막에 추가하고, 필요에 따라 부모 노드와의 위치를 교환하여 우선순위를 유지한다.
- 예시: 삽입 연산
- 데이터 삭제: 배열의 첫 번째 요소(우선순위가 가장 높은 요소)를 삭제한다. 삭제 후, 마지막 요소를 루트로 이동시키고, 자식 노드들과 비교하면서 우선순위에 맞게 재배치한다.
- 예시: 삭제 연산
Delete_q()을 수행할 때, 배열의 첫 번째 요소를 제거하고, 마지막 요소를 루트로 이동시킨 후, 우선순위에 맞게 하향식으로 재정렬한다.
- 예시: 삭제 연산

힙 추상 자료형
힙은 다양한 방식으로 구현될 수 있지만, 그 중에서도 우선순위 큐의 한 형태로서의 역할이 가장 중요하다. 우선순위 큐는 각 요소가 우선순위를 가지며, 우선순위가 높은 요소가 먼저 처리된다는 점에서 힙의 핵심적인 특징을 보여준다. 이러한 관점에서 힙은 우선순위가 높은 요소를 빠르고 효율적으로 접근할 수 있도록 설계된 자료구조로 볼 수 있다.
- 힙의 구조: 힙은 부모 노드가 자식 노드보다 우선순위가 높은 완전 이진 트리로 구성된다. 이는 힙에서 가장 높은 (또는 가장 낮은) 우선순위를 가진 요소가 항상 루트에 위치한다는 것을 의미한다.
- 힙의 연산: 힙은 주로 두 가지 기본적인 연산을 지원한다.
insert(element): 새로운 요소를 힙에 삽입한다. 삽입된 요소는 적절한 위치로 이동하여 힙의 속성을 유지한다.delete(): 힙에서 가장 우선순위가 높은 요소를 제거하고 반환한다. 이 과정에서 힙의 구조가 재조정되어야 한다.- 기타: peek(), isEmpty(), size()
- 힙의 응용: 힙은 운영체제에서의 작업 관리, 네트워크 트래픽 관리 등 다양한 분야에서 중요한 역할을 한다. 이는 작업의 우선순위에 따라 효율적으로 자원을 할당하고 관리하는 데 필수적이다.
typedef struct heap {
int heap[MAX_SIZE];
int size;
} heap;
int min_heapDelete(heap* h) {
int parent, child;
int data, temp;
data = h->heap[1];
temp = h->heap(h->size)--];
parent = 1; child = 2;
while (child <= h->size) {
if ((child < h ->size) && (h ->heap[child] > h -> heap[child+1])){
child++; }
if(temp <=h->heap[child]){
break;
}
h -> heap[parent] = h ->heap[child];
parent = child;
child *= 2;
}
h -> heap[parent] = temp;
return data;
}힙에서 삭제 연산
먼저 힙의 배열 표현에서는 부모 노드의 인덱스가 i일 때, 왼쪽 자식 노드의 인덱스는 2i, 오른쪽 자식 노드의 인덱스는 2i+1이다. 만약 자식이 i라면 부모는 i/2임을 숙지하자.
힙에서 삭제 연산은 힙의 특성을 유지하면서 가장 우선순위가 높은 데이터를 제거하는 과정이다. 최소힙을 예로 들면, 루트에 있는 가장 작은 값을 제거하고, 힙의 구조를 재조정하는 과정을 거친다.
삭제 과정은 다음과 같다:
- 삭제할 데이터 저장: 삭제될 루트 노드의 데이터를 저장한다. 이 데이터는 나중에 함수가 반환할 값이다.
- 마지막 원소 이동: 힙의 마지막 원소를 임시 저장소에 복사하고, 힙 크기를 줄인다. 이 원소는 임시로 루트 위치로 이동한다.
- 하향식 재정렬:
- 부모 노드에서 시작하여 자식 노드와 비교한다.
- 두 자식 중 더 작은 값과 부모 노드를 비교한다.
- 만약 임시 원소가 자식 노드보다 작거나 같으면, 해당 위치에 임시 원소를 삽입하고 과정을 종료한다.
- 그렇지 않으면 자식 노드를 부모 노드의 위치로 이동하고, 다음 자식 노드로 이동하여 과정을 반복한다.
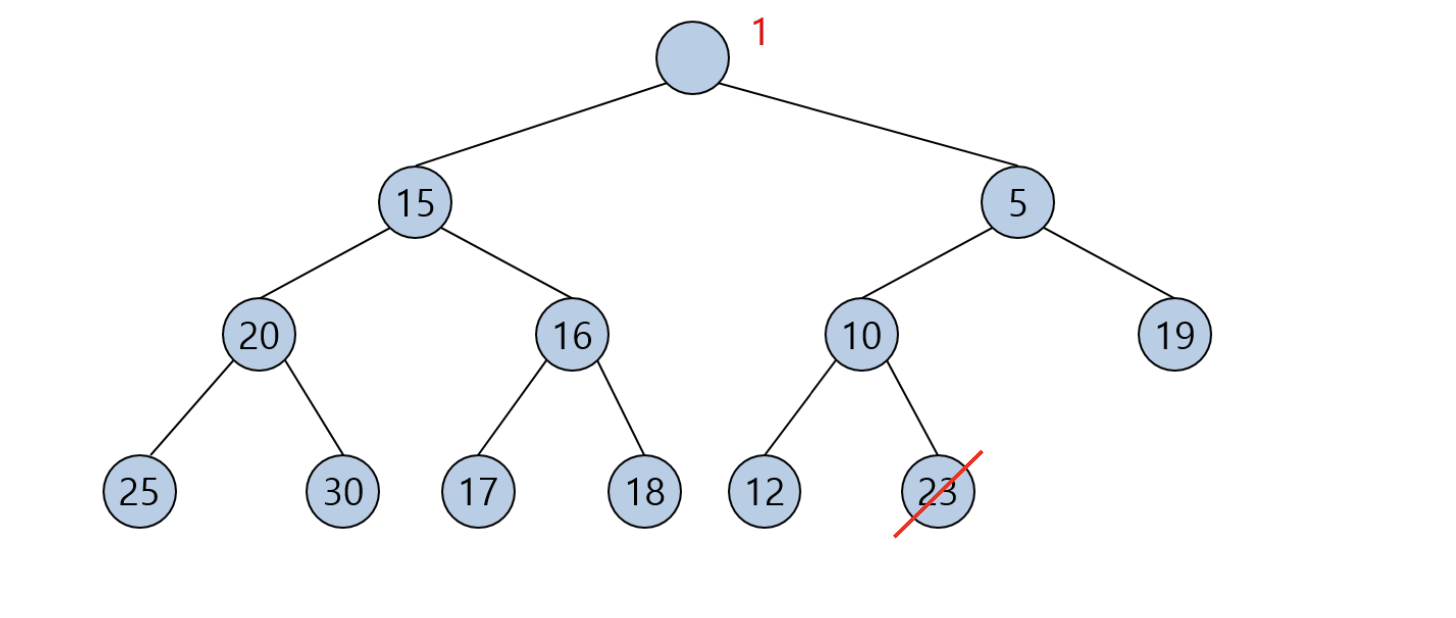
아래의 힙 배열에서 삭제 연산을 수행할 경우, 먼저 루트인 1이 제거되고, 마지막 원소인 23이 루트로 이동한다. 그 후, 23은 자식 노드들과 비교되면서 적절한 위치로 이동한다. 먼저 5와 비교하여 5가 더 작으므로, 5는 루트로 올라가고 23은 아래로 내려갑니다. 이 과정을 반복하여 23이 최종적으로 올바른 위치에 도달할 때까지 계속한다.




typedef struct heap {
int heap[MAX_SIZE];
int size;
} heap;
int min_heapDelete(heap* h) {
int parent, child;
int data, temp;
data = h->heap[1];
temp = h->heap(h->size)--];
parent = 1; child = 2;
while (child <= h->size) {
if ((child < h ->size) && (h ->heap[child] > h -> heap[child+1])){
child++; }
if(temp <=h->heap[child]){
break;
}
h -> heap[parent] = h ->heap[child];
parent = child;
child *= 2;
}
h -> heap[parent] = temp;
return data;
}힙에서 삽입 연산
힙에서의 삽입 연산은 새로운 데이터를 힙에 추가하는 과정이다. 이 과정은 힙의 특성을 유지하면서 새로운 데이터를 적절한 위치에 삽입해야 한다. 주로 다음과 같은 단계로 진행된다:
- 데이터 삽입: 새로운 데이터를 힙의 마지막 위치에 임시로 삽입한다.
- 상향식 재정렬:
- 삽입된 데이터를 부모 노드와 비교한다.
- 만약 삽입된 데이터가 부모 노드보다 우선순위가 높으면(최소 힙의 경우 작은 값), 부모 노드와 위치를 교환한다.
- 이 과정을 힙의 루트까지 혹은 더 이상 교환할 필요가 없을 때까지 반복한다.
void min_heapInsert(heap *h, int data){
int i;
i = ++(h ->size);
while(i !=1) && (item < h -> heap[i/2])) {
h-> heap[i] = h -> heap[i/2];
i/=2;
}
h -> heap[i] = data;
}
예를 들면, 최소 힙에 7이라는 값을 삽입하는 경우를 생각해 볼 수 있다. 처음에는 힙의 마지막 위치에 7을 임시로 삽입한다. 이후 7은 부모 노드인 12와 비교되어 교환되며, 계속해서 부모 노드와의 비교를 거치며 상향식으로 이동한다. 최종적으로 7은 5라는 부모 노드와 비교될 때, 5보다 크므로 이 위치에서 멈추고 최종 삽입 위치가 결정된다.

요약
- 힙은 무엇인가를 쌓아 놓은 더미이고, 항상 가장 위에 있는 것을 우선하여 꺼내는 구조를 상징한다. 그리고 힙은 우선순위 큐의 한 종류이다.
- 힙은 완전 이진 트리이며, 최소힙은 루트가 최소값이고 최대힙은 최대값이다.
- 최대힙은 트리의 모든 노드가 자식 노드보다 큰 값을 갖는 것이다.
- 최소힙은 트리의 모든 노드가 자식 노드보다 작은 값을 갖는 것이다.
- 힙에서 노드를 삭제한 후에도 완전 이진트리이어야 하며, 최대힙 혹은 최소힙 조건을 만족해야 한다.
참고 자료: 자료구조 (강태원, 정광식 공저, KNOU press 출판)
'CS > 자료구조' 카테고리의 다른 글
| 이진 탐색 트리Bs) - Splay, Avl, BB 트리 (1) | 2023.11.25 |
|---|---|
| 선택 트리, 숲, 이진 트리 개수 (2) | 2023.11.25 |
| 스레드 트리, 개념, 구현, 연산 (순회 삽입 삭제) (0) | 2023.11.24 |
| 트리 용어 및 개념, 이진 트리, 순회 연산, 생성 삭제 조회 연산 - 자바 코드 (0) | 2023.11.24 |
| 깊이 우선 탐색 (Depth-First Search) (0) | 2023.11.24 |



