Bs, Splay Avl, BB
개요
삽입, 삭제 연산을 보다 효과적으로 작업하기 위해 만든 이진 탐색 트리에 대한 정의와 순회 방법에 대해 학습한다. 이진 탐색 트리에서는 각 노드를 식별하기 위해서 별도의 일므을 붙인 '키'라는 용어를 사용한다. 노드의 데이터라고 생각해도 된다. 정해진 노드(vi)를 기준으로 왼쪽 서브트리에 있는 모든 노드는 vi의 키값보다 값이 작아야 하고, 오른쪽 서브트리의 노드들은 vi의 키값보다 값이 커야 한다는 조건을 만족하는 이진 트리를 이진 탐색 트리, 즉 BS 트리라고 한다.
균형 잡힌 트리로 Splay, AVL, BB 트리가 있다. Splay 연산을 적용한 Splay 트리는 최근에 사용한 노드 x를 다음에도 사용할 수 있다는 가정 하에 노드 x를 루트에 위치시켜 트리를 재구성한다. AVL 트리는 노드 Vi의 왼쪽 서브트리 높이와 Vi의 오른쪽 서브트리 높이가 최대 1만큼 차이가 난다는 조건을 만족하는 트리이다. 무게가 균형 잡힌 트리란 각 노드의 양쪽 서브트리 무게가 균형을 유지하는 트리이다. 이 트리를 BB 트리 (Bound-Balanced)라고 부른다. AVL 또는 BB 트리에 대하여 각각 높이 또는 크기 제한을 만족시키는 데 드는 비용은 트리를 완전히 균형 잡히게 유지하는 비용이나 노력보다 훨씬 작기 때문에 이런 트리를 사용한다.
1. 이진 탐색 트리 (BS 트리)
- 정의: 각 노드에 '키'를 할당하여, 왼쪽 서브트리는 현재 노드의 키값보다 작고, 오른쪽 서브트리는 현재 노드의 키값보다 크도록 구성된 이진 트리.
- 특징:
- 키의 개념을 도입하여 노드를 쉽게 식별.
- 트리의 모든 노드는 유일한 키를 가짐.
- 삽입, 삭제 시 트리의 구조를 유지해야 함.
- 순회 방법:
- 전위, 중위, 후위 순회로 탐색 가능.
- 특히, 중위 순회를 통해 키의 오름차순으로 데이터 접근 가능.
- 탐색 알고리즘: 키값 비교를 통해 빠르게 원하는 노드를 찾음.
- 삽입 및 삭제: 삽입은 항상 잎 노드로, 삭제 시 서브트리 구조 유지에 주의 필요.
트리에 특정 데이터가 있는지 검색하고, 노드를 자주 삽입, 삭제하는 응용 문제에 가장 효과적인 이진 트리가 지금 부터 설명하는 이진 탐색 트리이다. 이름에서 알 수 있듯이 BS 트리는 탐색에 최적화된 트리로 생각하면 된다. 탐색에 최적화되다 보니 이 트리에서는 '키'라는 용어가 등장한다. 사실 키는 노드의 데이터라 생각해도 무방하다. 일반적으로 트리의 각 노드에 저장된 데이터는 매우 다양할 수 있다. 대부분의 자료구조 서적에서 트리의 노드는 숫자나 영어 알파벳 정도로 간단하게 표기한다. 그러나 실제로 응용될 때는 각 노드가 하나의 거대 레코드 문서이거나, 음악, 영화 파일 일 수도 있다. 이 경우 각 노드를 식별하기 위해서는 별도의 간딘한 이름을 붙여주는 것이 좋다. 그것이 키이다. 그러니까 이제부터 루트 노드 v의 키값이 3이라든지 A라던지 하는 표현을 사용할 수 있다.
BS 트리를 정의해보자.
노드 vi의 키를 ki라 할 때 각 노드 vi가 다음을 만족하는 이진 트리를 이진 탐색 트리, 즉 BS 트리라고 한다.
1) vi의 왼쪽 서브트리에 있는 모든 노드의 키값은 vi의 키값보다 작다.
2) vi의 오른쪽 서브트리에 있는 모든 노드의 키값은 vi의 키값보다 크다.
다음과 같은 그림에서 원 안의 알파벳이 해당 노드의 키값이다. 예를 들어 "루트 노드의 키값은 B이고 왼쪽 자식 노드의 키값은 A이다"라고 표현할 수 있는 것이다. 그러면 이 이진 트리는 위 조건을 만족하는 BS 트리이다.
B - A
A - B
B - A
B - D
D - C
C - D
순서가 같은 키에 대해 BS 트리가 유일하지는 않다. 즉, 같은 순서 데이터에 대해 BS 트리를 다양하게 만들 수 있다는 것이다.
다음과 같이 순서 데이터 A, B, C, D를 유지하는 다른 BS 트리가 가능하다.
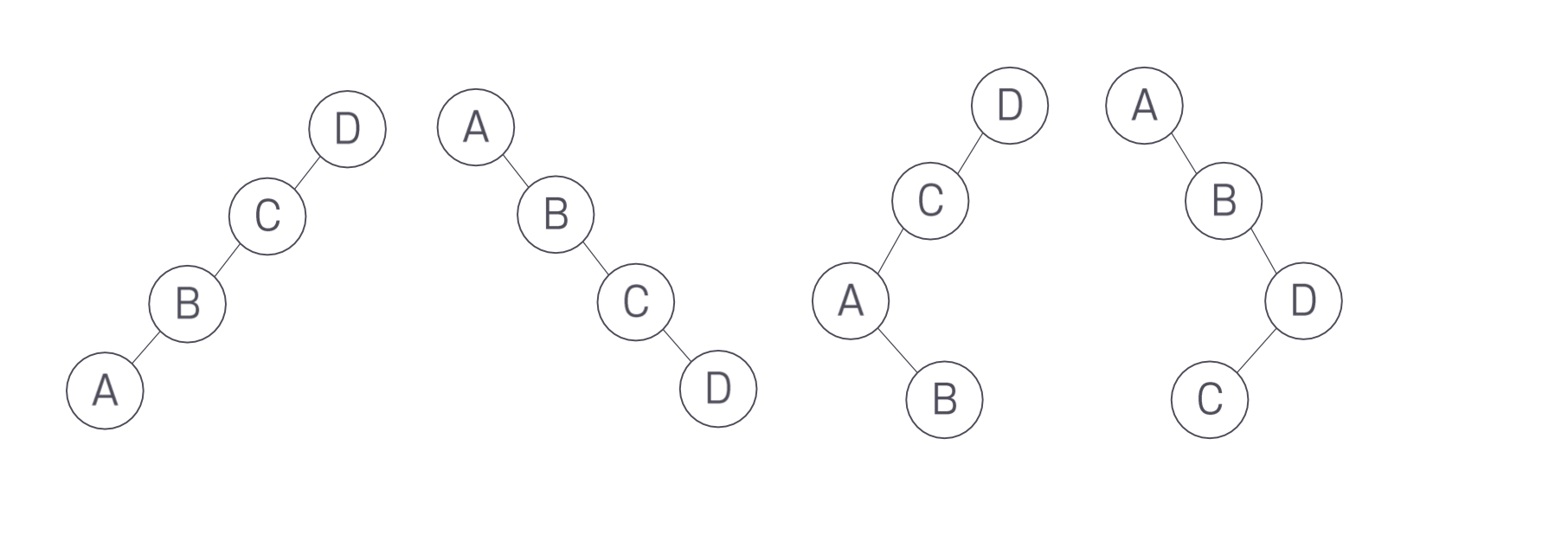
1) 트리 순회
BS 트리는 전위 순회, 중위 순회 및 후위 순회로 모든 정점을 차례로 순회할 수 있도 트리 내의 특정 정점을 탐색할 수도 있다. BS 트리를 중위 순회하는 코드는 다음과 같다.
typedef struct BSTnode{
struct BSTnode* left;
char key;
char content[10];
struct BSTnode* right;
} BSTnode;
void inorderBST(BSTnode* root){
if (root != null) {
inorderBST(root->left);
printf("%c", root->key);
inorderBST(root ->right);
}
}먼저 노드 타입을 보면 왼쪽, 오른쪽 자식을 위한 포인터와 데이터 필드 content[] 외에 키값을 위한 문자 변수 key 가 있음을 알 수 있다.
사실 더 중요한 것은 데이터, 즉 content[] 에 저장할 내용이다. 여기서는 노드 구조를 간단하게 보여 주기 위해서 문자 10개를 저장하는 것으로 했지만 이 자리에 영화나 용량이 큰 문서가 저장되는 것이다. 키 값은 간단한 문자 변수로 정의했다. 순회함수는 간단하다. 트리의 루트 포인터를 매개변수로 하는 중위 순회 함수 inorderBST()는 왼쪽 서브트리를 모두 순회한 후 루트를 방문하고 오른쪽 서브트리를 모두 순회한다.
중위 순회 알고리즘은 상대적으로 전위 순회나 후위 순회보다 순환으로 구현하기가 쉽다.
2) 트리 탐색
BS 트리는 탐색에 최적화한 트리이다. 당연히 어떤 키값을 갖는 노드가 그 트리에 있는지 아닌지를 아주 빠르게 확인할 수 있다. 노드 vi의 키를 ki라 할 때 BS 트리에서 키값이 k인 노드를 찾는 과정은 다음과 같다.
1) 트리가 비어 있다면 탐색 실패, 아니면 K와 현재 루트 노드의 키값 ki를 비교한다.
2) k = ki이면 탐색 성공, 이때 찾은 정점은 vi이다.
3) k<ki이면 vi의 왼쪽 서브트리 탐색. 즉 vi=vi,left로 바꾸고 1)로 간다.
4) K>ki이면 vi의 오른쪽 서브트리 탐색. 즉 ,vi=vi,right로 바꾸고 1)로 간다.
BSTnode* searchBST(BSTnonde* root, char key){
if(root == null) {
printf("Error");
return root;
}
if (key == root -> key) {
return root;
} else if (key <root->key){
searchBST(root->left, key);
} else if (key > root -> key){
searchBST(root -> right, key);
}
}위의 코드는 BS 트리의 노드 탐색을 보여준다. 먼저 BS 트리 탐색 함수 searchBST()는 트리의 루트 노드에 댛한 포인터 Root와 키값 key를 매개변수로 받아 탐색에 성공핳면 해당 노드의 포인터를 반환하고 실패하면 null을 반환한다.
탐색 과정은 간단하다. 매개변수로 전달받은 키와 현재 루트의 키를 비교해서 같으면 그때의 포인터를 반환하고, 아니면 값의 차이에 따라 오른쪽이나 왼쪽 서브트리의 루트를 매개변수로 하여 순환 호출을 한다. BS트리는 현재 노드의 키값을 기준으로 왼쪽에는 키값이 작은 것들, 오른쪽에는 큰 것들만 저장되어 있으므로 다음 탐색 위치가 오른쪽인지 왼쪽인지를 쉽게 판단할 수 있는 것이다. 한 번의 비교로 전체 데이터의 절반을 탐색 대상에서 제외하므로 빠르게 탐색할 수 있는 것이다.
3) BS 트리 삽입 및 삭제
이진 탐색 트리에서 새 노드는 항상 잎으로 삽입한다. 이것을 꼭 기억하자. 즉 루트부터 키값을 비교하여 자기가 삽입될 위치가 왼쪽이냐 오른쪽이냐를 정하며 내려간다. 그러다 Null에 도달하면 그 값을 자기를 가리키도록 하면 그만이다. 어떤 포인터가 null이라는 것은 자식이 없다는 것이고, 그 포인터가 자기를 가리키면 거기에 매달리는, 즉 자식이 되는 것이다.
물론 키 값이 같은 노드를 발견하면 삽입 과정을 종료한다. 이미 있는데 또 넣을 필요는 없는 것이다.
계속 값을 비교하며 내려간다는 점에서 삽입 알고리즘은 탐색 알고리즘과 유사하다.
1) k= ki이면 멈춘다.
2) k < ki이면 vi의 왼쪽 서브트리에 삽입해야 하므로 vi = vi->left로 하고 4)로 간다.
3) K> ki이면 vi의 오른쪽 서브트리에 삽입해야 하므로 vi = vi->right로 하고 4)로 간다.
4) 트리가 비어 있으면 키 k를 가지는 노드를 삽입한다. 그렇지 안흥면 다시 k와 현재 루트 노드의 키 Ki를 비교하며 탐색을 반복한다.
즉 노드는 4) 단계에서 삽입한다.
삽입할 위치를 찾아 내려가다 보면 마침내 잎에 도달한다. 그러면 잎의 키와 비교해서 자신이 위치할 곳이 왼쪽인지 오른쪽인지를 결정할 수 있다. 그럼 그리로 내려간다. 그곳이 바로 null 포인터가 있는 곳이다.
그러면 다음 그림을 보자. A와 F를 추가로 삽입하는 경우 어떻게 될까?
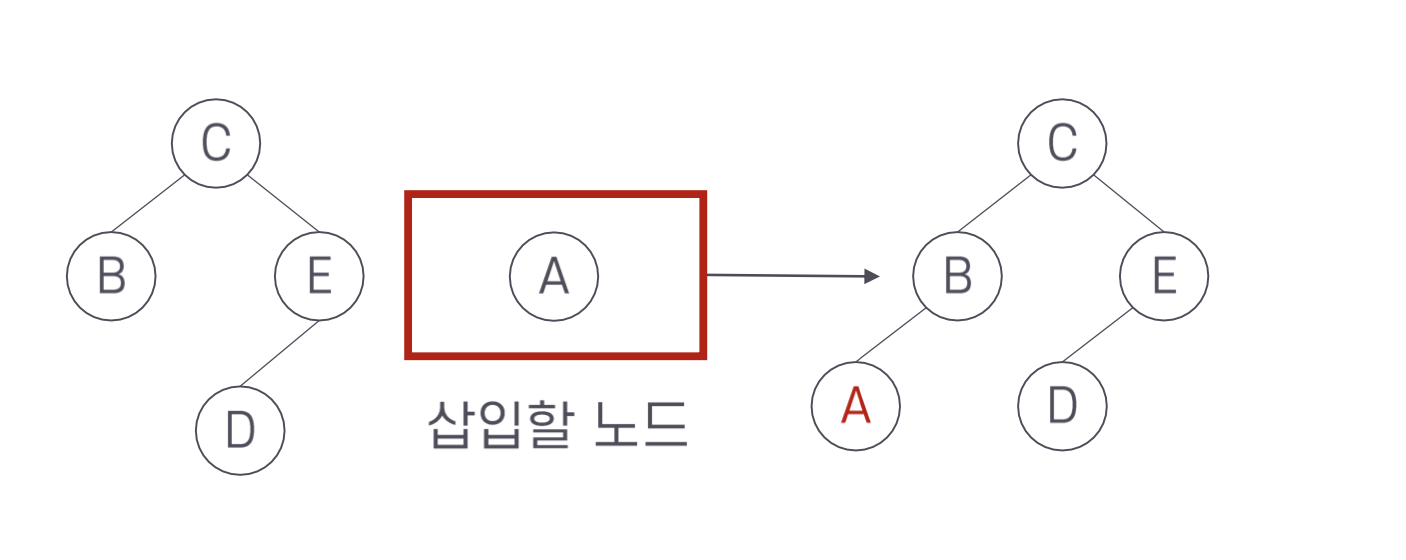
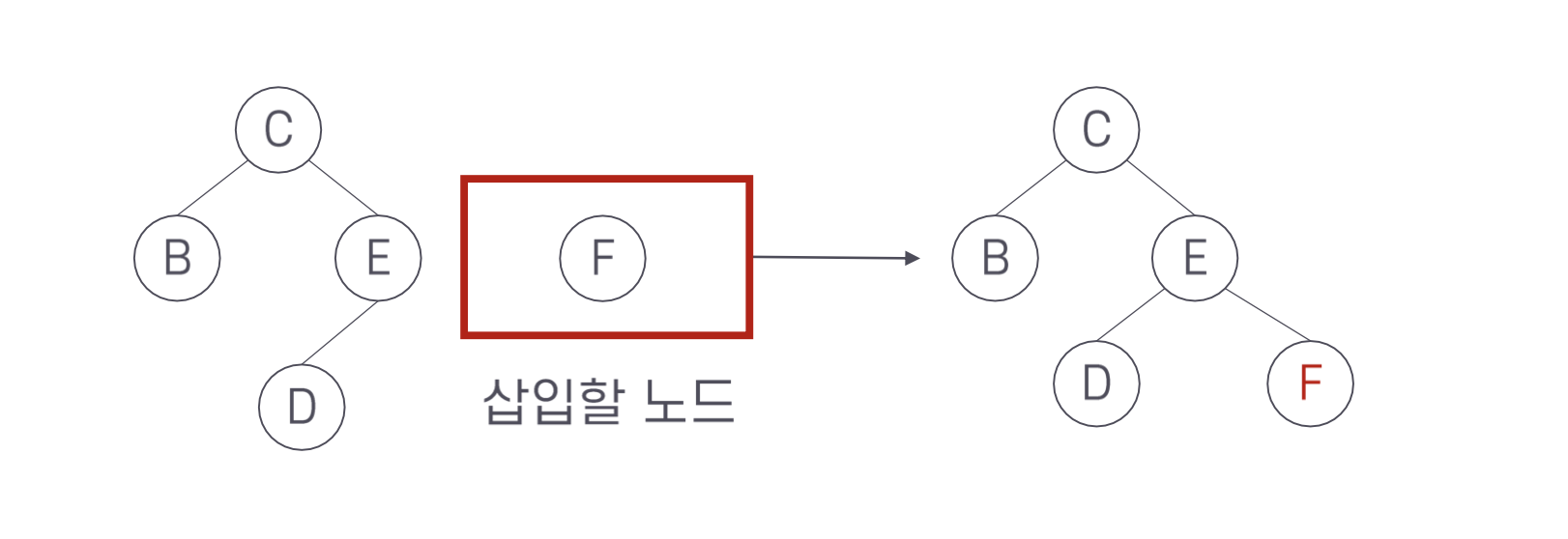
키 A는 C보다 그리고 B 보다 작으므로 왼쪽으로 내려가 잎 노드의 왼족에 삽입한다. 반면에 키 F는 C 보다 그리고 E 보다 크므로 키가 E인 노드의 오른쪽에 삽입하는데 이 노드는 잎은 아니다. 그러나 삽입할 위치인 오른쪽에 자식이 없다. 즉, 오른쪽 자식을 가리키는 포인터가 Null 이다. 따라서 단계 1)에 의해 키 F를 가지는 노드를 삽입한다.
BS 트리의 루트 포인터 Root와 key를 매개 변수로 하는 insertBST()코드는 다음과 같다.
탐색에서는 실패 상황이 삽입에서는 삽입 시점이 된다. 마찬가지로 탐색 성공이 삽입에서는 종료 조건이 된다.
BSTNode* inserBST(BSTnode* root, char key) {
BSTNode* ptr,
BSTnode* newNode = (BSTNode*)malloc(sizeof(BSTnode));
newNode -> key =key;
newNode -> left = newNode -> right = null;
if (root == null) {
root = newNode;
return rootl
}
ptr = root;
while(ptr) {
if(ikey == ptr ->key) {
print("error: 중복 값은 허용되지 않습니다.");
return root;
} else if (key < ptr -> key ) {
if (ptr -> left == null) {
ptr ->left = newNode;
return root;
} else {ptr =ptr->left;}
} else {
if (ptr -> right == null) {
ptr -> right = newNode;
return root;
} else {ptr = ptr->right}
}
}
}BS 트리에서 삭제하려는 노드가 잎이 아닌 경우 그 노드의 서브트리를 유지해야 하므로 삭제 과정 역시 복잡하다.
다음과 같은 트리에서 노드를 삭제하는 경우를 생각해 보자.
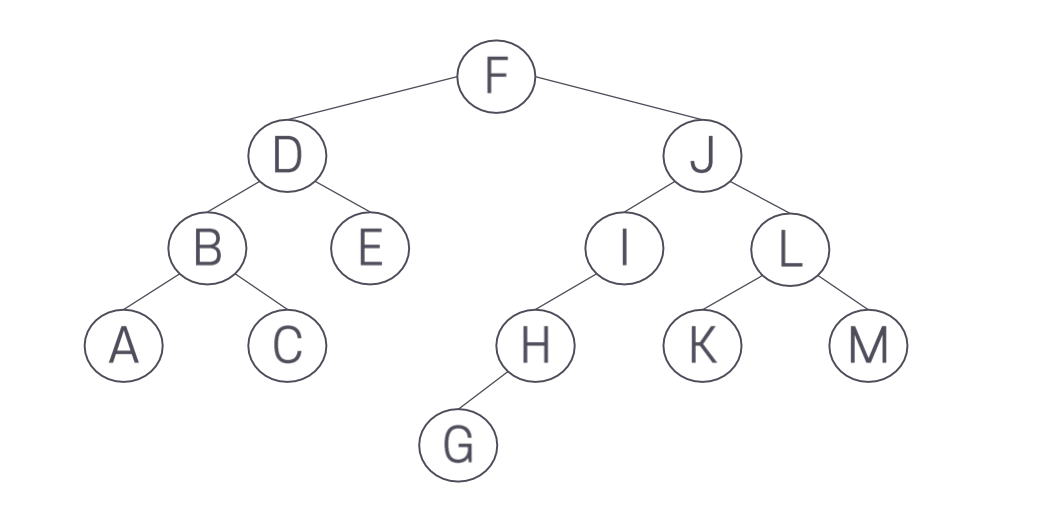
노드 H를 삭제하는 경우 어떨까 이때 G를 처리해야 한다. 다행이 이 경우는 노드의 H 위치, 즉 노드 I의 왼쪽 서브트리가 되게 설정할 수 있다. 마찬가지로 I를 삭제한다면 H를 J의 왼쪽 서브트리로 지정하면 된다. 결국 한쪽 서브트리가 null인, 즉 자식을 하나만 갖는 노드를 삭제하는 경우, 그 노드의 Null이 아닌 서브트리의 루트를 삭제한 노드를 가리키던 포인터에 할당하면 된다.
노드 L을 삭제하는 경우는 어떨까? L은 두 개의 서브트리 K와 M을 가지고 있다. 그렇다면 둘 중 어느 것을 위로 올릴까? 다행히 이 경우는 K와 M중 어느 것을 L의 자리에 옮겨도 된다. 즉, BS 트리의 조건을 어기지 않는다.
노드 F의 삭제는 더 어렵다. BS 트리의 조건을 만족시키면서 이동해야 하므로, 왼쪽 서브 트리에 있는 노드 중에서 가장 큰 값을 가지는 노드를 선택하거나, 오른쪽 서브 트리의 가장 작은 노드를 선택해 옮겨야 한다. 왼쪽 서브 트리에서 선택하면 노드 F를 삭제한 후 왼쪽에서는 E가 선택될 것이다. 오른쪽에서 선택한다면 가장 작은 G가 선택될 것이다. 이렇게 둘 중 한가지 방법을 선택해 일관성 있게 적용하면 두 자식 노드를 가지고 있는 경우에도 노드를 삭제할 수 있다.
if (del ->left == null && del ->right == null ) { // 자식 노드가 0개인 경우
if (parent !=null) {
if (parent ->left == del) {
parent -> left = null;
} else {parent ->right = null;}
} else {root = null;}
} else if (del ->left != null && del -> right != null) { // 자식 노드 2개인 경우
predecessor = del;
successor = del -> left;
while (successor ->right != null ) {
predecessor = successor;
successort = successor -> right ; }
if (predecessor -> left == successor ) {
predecessor ->left = successor -> left;
} else { predecessor ->right =successor ->left; }
del -> key =successor -> key;
del = successor;
} else { // 자식 노드 1개
if (del ->left != null ) {
child = del ->left;
} else { child = del -> right; }
if (parent != null) {
if (parent -> left == del){
parent -> left = child;
} else { parent ->right = child; }
} else {
root = child;
}
} 복잡한 문제를 피해가는 방법으로 그냥 삭제한 노드를 삭제한 것으로 표시하고 트리에 내버려 두는 방법도 있다. 이후에 탐색이나 삽입시 표시된 노드의 키는 트리 순회에만 참여하고 노드로서 무시하는 것이다.
적당한 휴리스틱 알고리즘
최적의 BS 트리가 적당한 휴리스틱을 통해 구축한 알고리즘을 사용할 때 가능하다는 것이 많은 연구 결과로 밝혀졌다. 즉, 휴리스틱 알고리즘으로 생각보다 쉽게 쓸만한 이진 탐색 트리를 구성할 수 있다는 것이다. 그 예는 다음과 같다.
1) 자주 탐색하는 키를 가진 노드를 트리의 루트에 가깝게 놓는다.
2) 트리가 균형이 되도록 유지한다. 즉, 각 노드에 대해 왼쪽과 오른쪽 서브트리가 가능한 한 같은 수의 노드를 갖게 한다.
이와 같은 휴리스틱을 반영한 트리가 Splay, AVl, BB 트리이다.
2. SPLAY 트리
Splay 트리는 자주 탐색하는 키를 가진 노드를 후트에 가깝게 위치하도록 구성한 Bs 트리이다. 이 트리는 Splay 연산을 적용해 최근에 접근한 노드 x를 루트에 위치시켜 트리를 재구성한다.
다음 그림은 트리를 재구성하기 위해 Splay를 연속으로 적용하는 것을 보여준다. 즉 가장 최근에 사용한 노드 x가 트리의 루트에 올 때까지 Splay 연산을 반복하여 적용한다.
노드 g는 최근에 접근한 노드이고, 노드 p는 x의 부모 노드, g는 x의 조부모 노드이다.
1) zig: p가 트리의 루트이면 p와 x의 간선 연결을 회전 시킨다.
2) zig-zig: p가 루트가 아니고 x와 p가 동일하게 왼쪽 자식 또는 오른쪽 자식이면 p와 조부모 g와의 간선 연결을 회전시키고, 그 다음에 x와 p의 간선 연결을 회전시킨다.
3) zig-zag: 만약 p가 루트가 아니고 x가 왼쪽 자식, p가 오른쪽 자식(또는 그 반대)이면 x와 p의 간선 연결을 회전시키고, 그 다음에 x와 x의 새로운 부모 p와의 간선 연결을 회전시킨다.
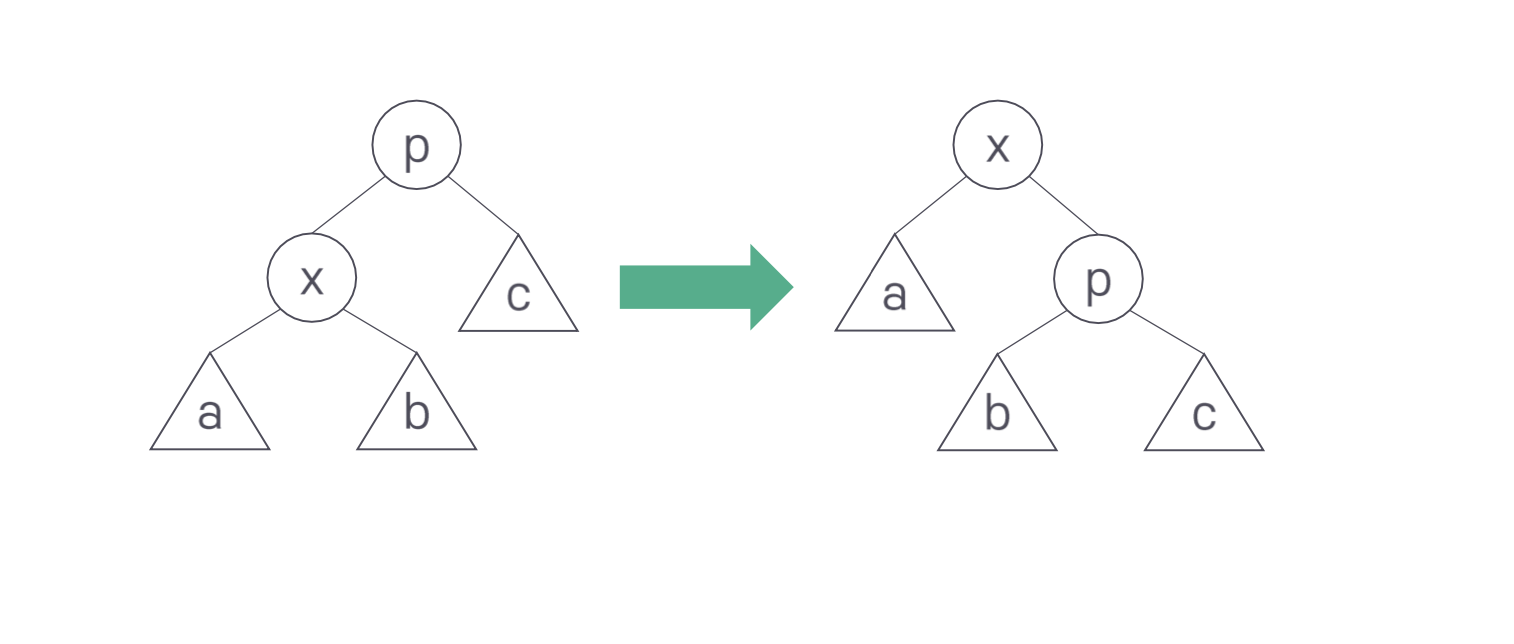
위의 그림은 zig 회전 수행 전과 후의 그림이다.
회전은 3단계로 진행된다. 먼저 x-a가 p-x 자리로 올라간다. 이때 서브트리 b는 연결이 끊어진다. 대신 p-c가 오른쪽 아래로 내려간다. 이때 전 단계에서 올라온 x와 p를 연결한다. 마지막으로 첫 단계에서 연결이 끊긴 서브트리 b를 p의 왼쪽 서브트리로 연결한다.
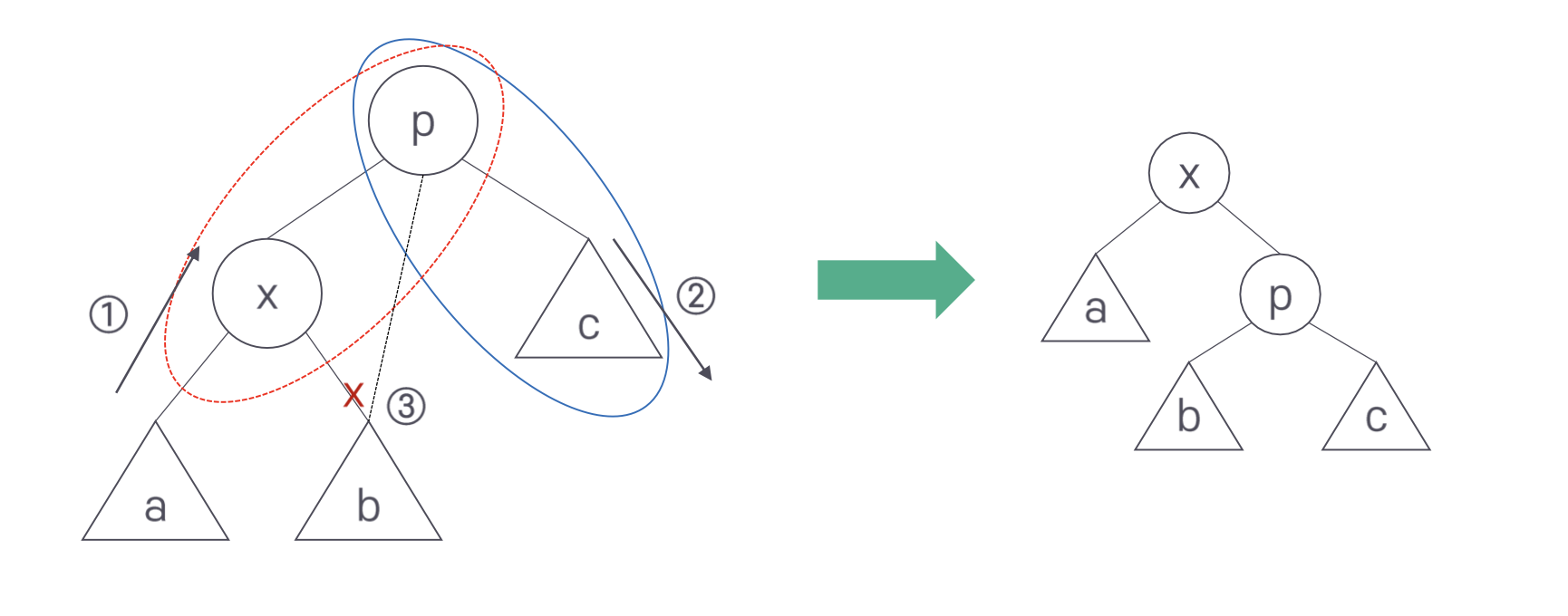
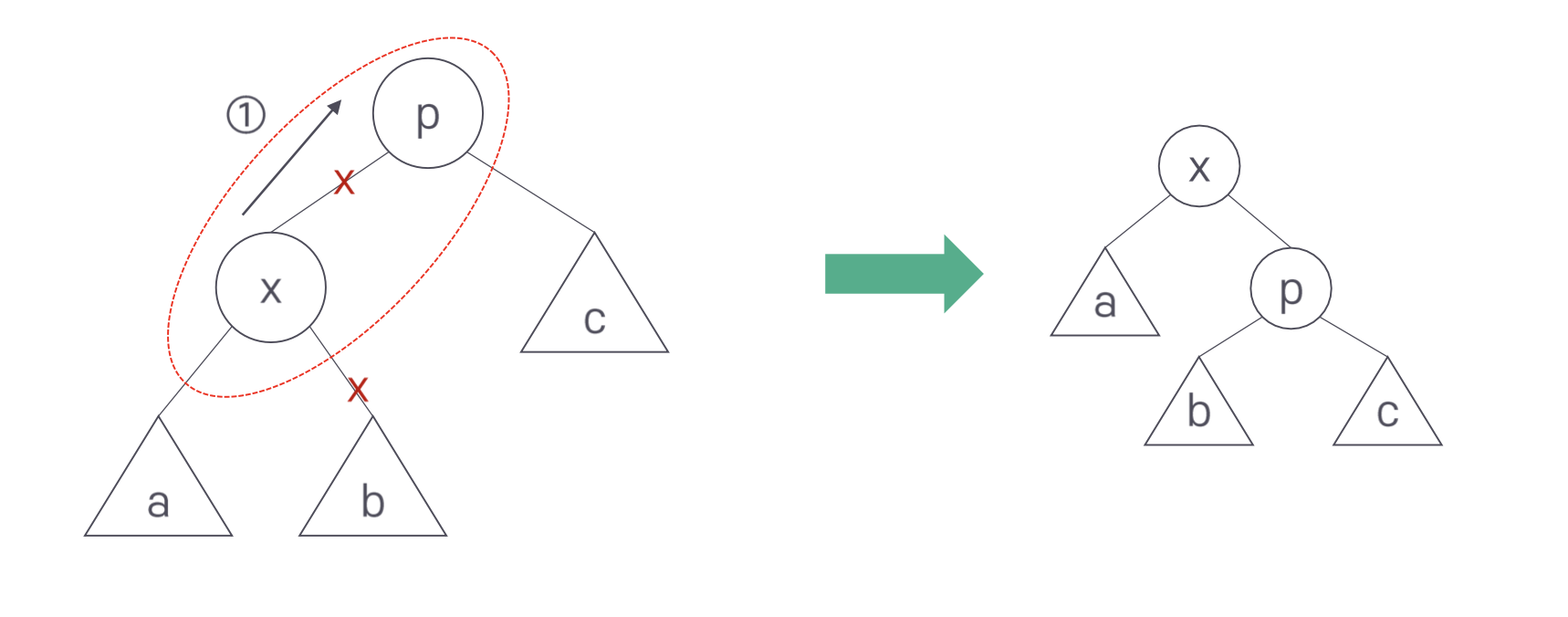
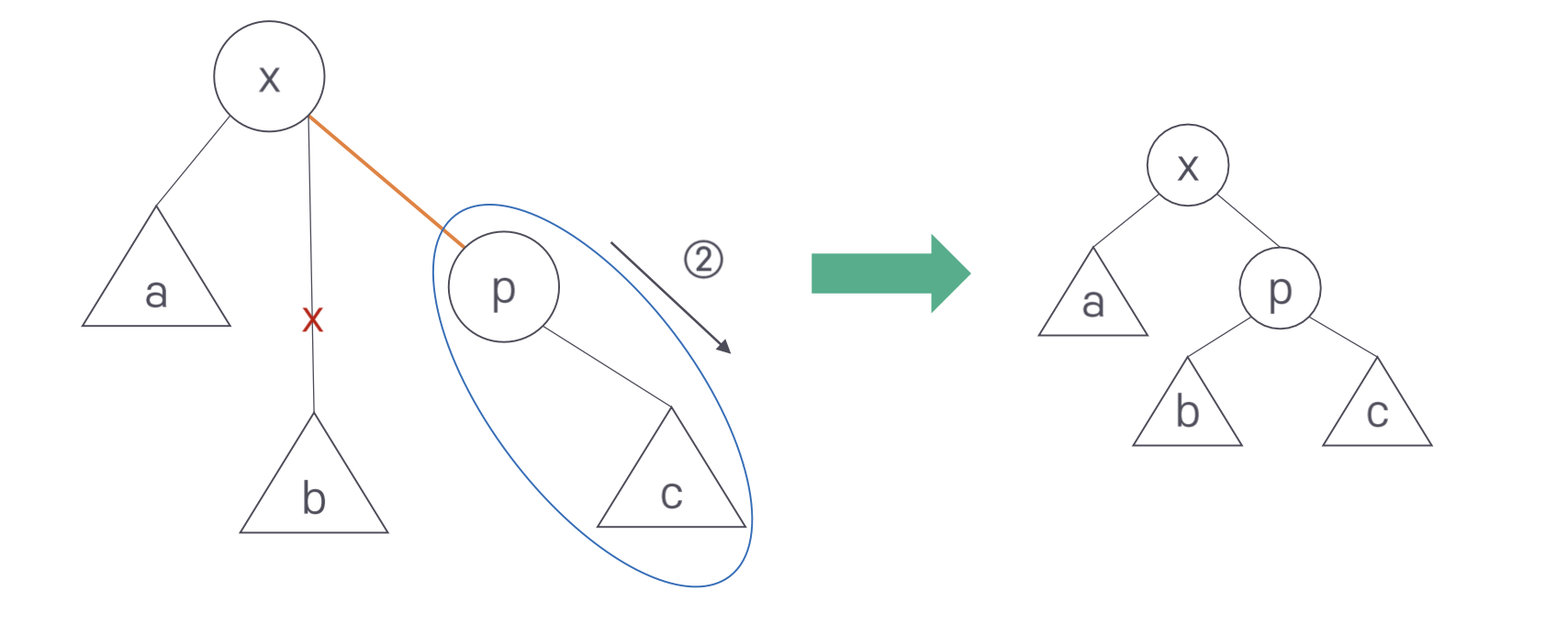
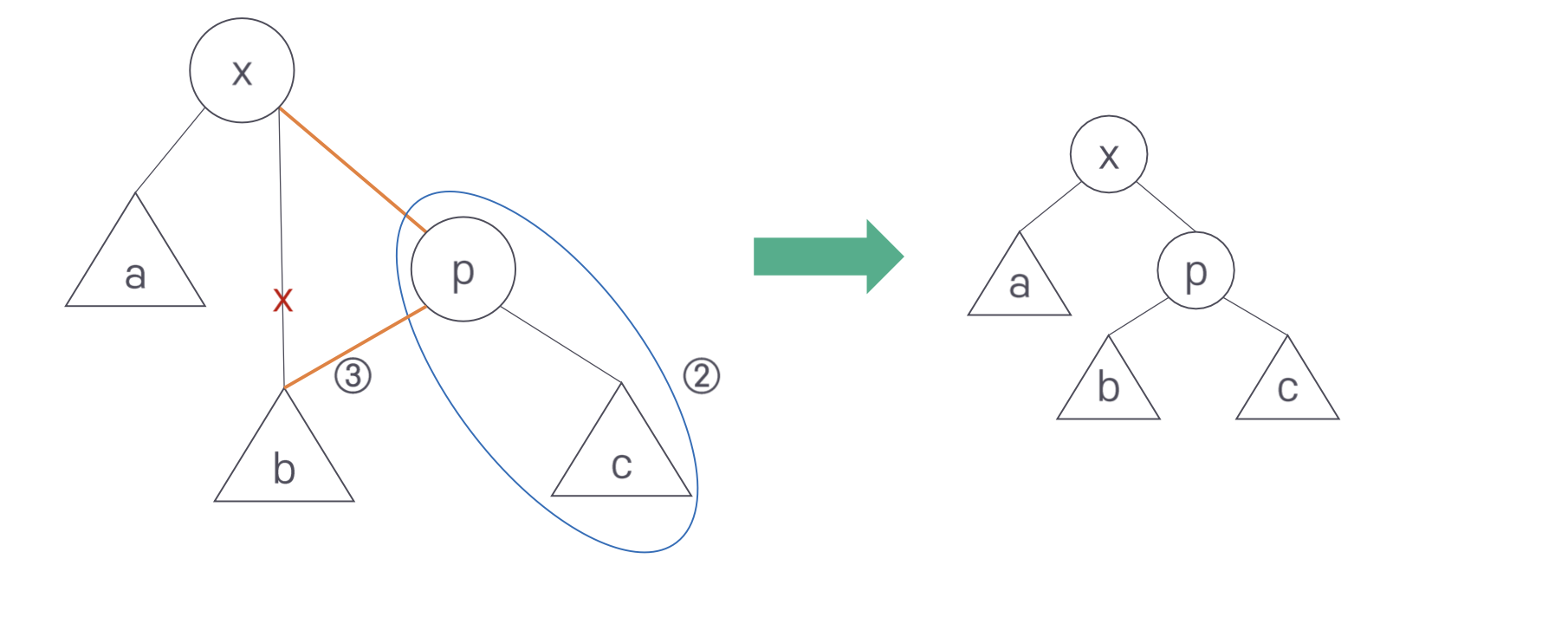
zig-zig와 zig-zag의 회전도 같은 방식으로 생각하면 된다.
중요한 것은 노드 x가 트리의 루트에 위치한다는 것이다. 즉, 자주 사용ㅎ하는 것은 앞으로 자주 사용할 것이라는 전제하에 특정 노드에 어떤 형태로든 접근하면 그 노드를 Splay를 적용하여 루트에 올려놓는다는 것이 Splay 트리의 핵심이다.
다음과 같은 상태에서 7을 위로 올리는 연산을 생각해보자.
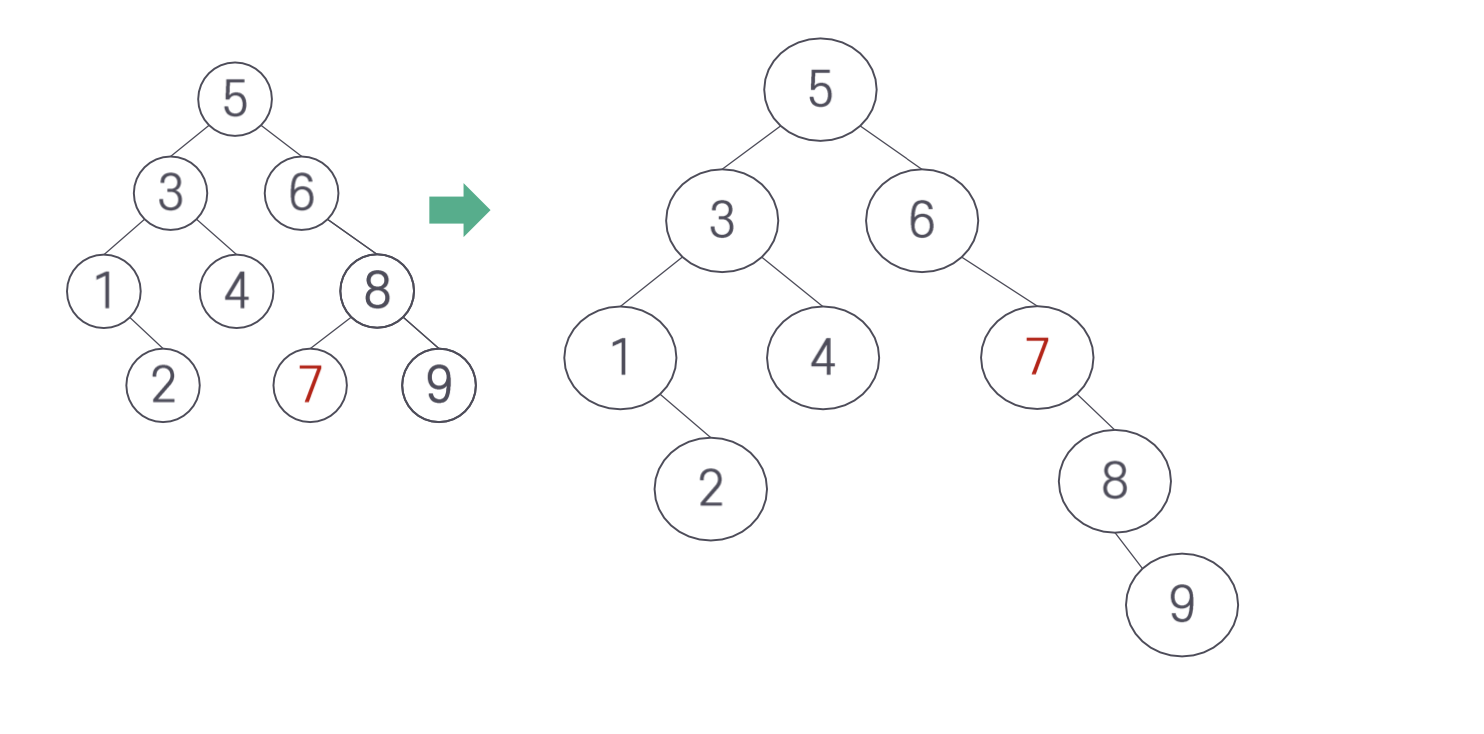

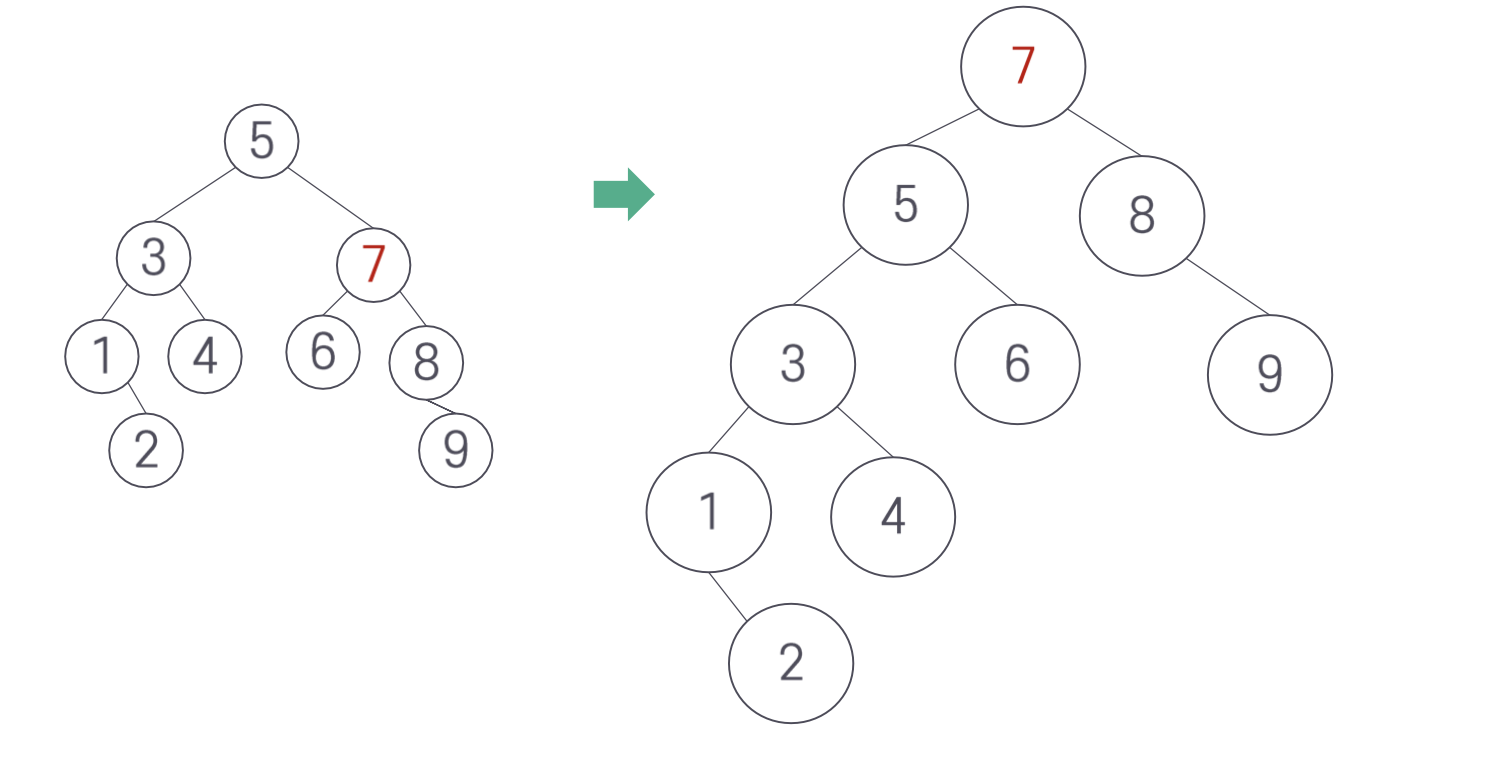
3. AVL 트리
두 번째 휴리스틱을 적용한 트리 부류는 첫 번째 휴리스틱보다 더 성능이 좋다고 알려져 있다. 그러나 노드의 삽입과 삭제가 일어날 때, 노드 키값과 서브트리 키 값 사이의 관계를 유지하며 규형을 유지하는 것이 쉽지 않다.
예를 들어 다음 노드에 8을 삽입하는 것을 생각해보자. 노드 8을 노드 7의 오른쪽 서브트리가 되도록 연결하면 된다.
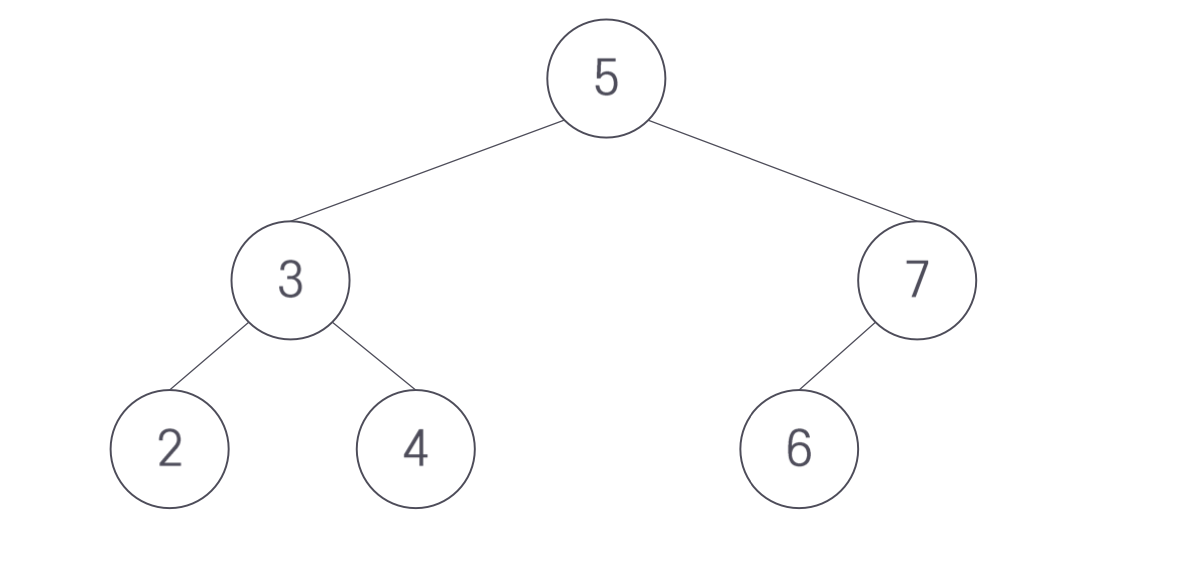
그러나 같은 트리에 노드 1을 삽입하면 문제가 다르다. 노드 1의 삽입 위치는 노드 2의 왼쪽 서브트리가 되어야 하며 이 경우 균형이 깨진다. 노드 7의 오른쪽이 비기 때문이다.
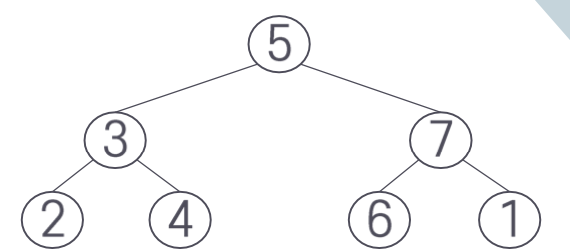
BS 트리의 탐색 성능을 개선하면서 균형을 유지하는 데 따르는 수고를 줄이려면 제한 조건을 완화하여 트리가 완전한 균형이 아닌 것을 허용해야 한다. 이러한 조건에 맞는 변형 BS 트리가 AVL 트리와 BB 트리이다.
AVL은 이 개념을 제안한 수학자의 이름 앞 글자를 따서 붙은 이름이다. 이 트리는 거의 완전한 균형 트리의 한 형태로 높이가 균형 잡힌 '높이 균형 트리'이다. 트리의 각 노드 vi에 대해서 다음과 같은 성질을 마족할 때 그 트리는 '높이가 균형 잡혔다'라고 한다.
AVL 조건 : 노드 vi의 왼쪽 서브트리 높이와 vi의 오른쪽 서브트리 높이가 최대 1만큼 차이가 난다.
트리의 높이란 노드가 가질 수 있는 가장 높은 레벨에 1을 더한 값이므로, 즉 루트로부터 잎까지 가장 긴 경로 길이를 말한다. 따라서 다음과 같은 BS 트리는 모두 높이가 균형 잡힌 트리라고 볼 수 있다.
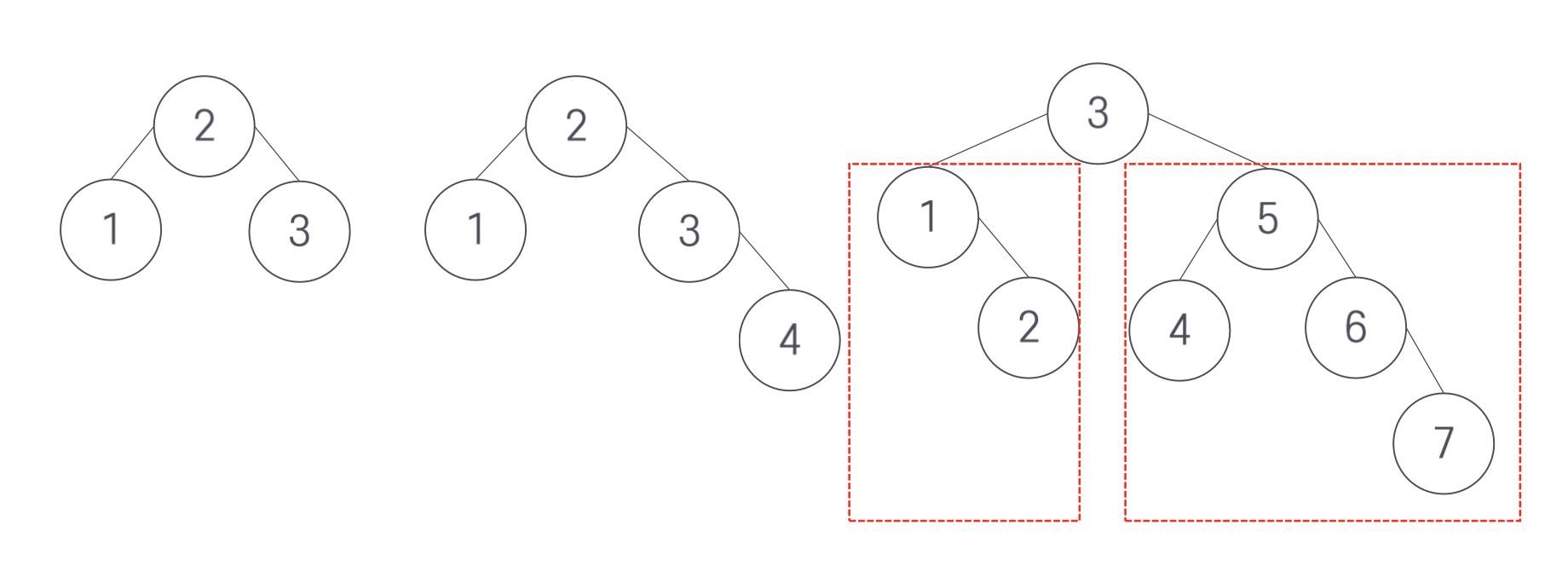
반면 불균형한 트리는 다음과 같다.

AVL 트리는 직접 탐색 성능이 매우 좋다. 비록 AVL 트리가 완전히 균형 잡힌 트리보다 덜 균형 잡혔지만 탐색 경로의 길이는 크게 다르지 않은 것으로 알려져 있다. 그러므로 AVL 트리는 완젆히 균형 잡힌 트리에 거의 가까운 좋은 성능을 가진다. 만약 삽입이나 삭제 수행으로 AVL 트리의 균형이 깨지면 균형 잡힌 상태로 다시 재구성해야 한다.
3. BB 트리
거의 완전히 균형 잡힌 또 다른 트리는 BB 트리이다.
무게가 균형 잡힌 트리라고 하여 Bound-Balanced tree라고 부른다. 무게 균형 트리는 각 노드의 양쪽 서브트리 무게가 균형을 유지하는 트리이다. 구체적으로 임의의 노드 x에 대해 다음 식이 만족핳ㄴ다.
BB 트리 : 루트2 -1 < 왼쪽 서브트리의 무게 / 오른쪽 서브트리의 무게 < 루트 2 + 1
무게가 균형 잡힌 트리의 기본 개념은 완전히 균형 잡힌 것으로부터 얼마나 벗어날 수 있는가에 제한 조건을 준 것이다. 제한 조건은 왼쪽 서브트리와 오른쪽 서브트리에서 총 노드 개수의 차이를 말한다. 즉, 서브트리의 높이가 아닌 서브트리의 노드 개수에 제한을 둔 것이다. AVL 트리는 키를, BB 트리는 무게라는 개념을 사용하지만 두 트리 모두 짧은 탐색 길이와 균형 요구를 충족하는 데 목적을 두고 있다.
BB 트리에서 균형 제어를 인수 베타에 대해, 베타가 1/2이면 왼쪽 서브트리와 오른쪽 서브트리는 같은 노드를 가진 상태이다. 만일 베타가 1/4이면 한쪽 서브트리는 다른 쪽 서브트리에 비해 세 배 정도 노드를 많이 갖는 것이 허용되는 것이다.
그렇다면 삽입이나 삭제시 다시 완전히 균형 잡히게 유지하는 비용이 어느 정도일까? AVL과 BB 모두 O(log2n)으로 일반 트리의 O(n)보다 나은 성능을 보이는 것으로 알려져 있다.
요약
- 트리에 특정 데이터가 있는지 검색하고, 노드를 자주 삽입, 삭제하는 응용 문제에 가장 효과적인 이진 트리는 이진 탐색 트리이다.
- 키는 각 노드를 식별하기 위해 별도의 간단한 이름을 붙여준 것으로 노드의 데이터라고 생각할 수 있다.
- 이진 탐색 트리에 대해 전위, 중위 및 후위 순회로 모든 정점을 차례로 순회할 수 있고, 트리 내의 특정 정점을 탐색ㅎ할 수도 있다.
- 이진 탐색 트리에서 새 노드는 항상 잎으로 삽입한다. 즉, 루트부터 키값을 비굫하며 자기가 삽입될 위치가 왼쪽이냐 오른쪽이냐를 정하며 내려간다.
- Splay 트리는 자주 탐색하는 키를 가진 노드를 루트에 가깝게 위치하도록 구성한 이진 탐색 트리이다.
- Splay 트리는 Splay 연산을 적용하여 최근에 사용하려고 접근한 노드 x를 루트에 위치시켜 트리를 재구성한다.
- AVL 트리는 노드 vi의 왼쪽 서브트리 높이와 vi의 오른쪽 서브트리 높이가 최대 1만큼 차이가 난다는 조건을 만족하는 트리이다.
- 트리의 높이란 노드가 가질 수 있는 가장 높은 레벨에 1을 덯한 값으로 루트로부터 잎까지 갖아 긴 경로 길이를 말한다.
- 트리의 무게는 트레이 속한 잎 노드의 개수로 정의한다.
- 무게가 균형 잡힌 트리 BB 트리란 각 노드의 양쪽 서브트리 무게가 균형을 유지하는 트리이다.
- AVL 또는 BB 트리에 대해 각각 높이 또는 크기 제한 조건을 만족시키는 데 드는 비용은 트리를 완전히 균형 잡히게 유지하는 비용이난 노력보다 훨씬 작다.
- 삽입이나 삭제 후에 트리를 완전히 균형 잡히게 유지하기 위해서는 O(n) 개의 노드를 옮겨야 하는데, AVL 또는 BB 트리는 O(log2n)개의 노드를 옮기면 되는 것으로 알려져있다.
참고 자료: 자료구조 (강태원, 정광식 공저, KNOU press 출판)
'CS > 자료구조' 카테고리의 다른 글
| 멀티웨이 탐색 트리 2 : 2-3 트리, 2-3-4 트리, 레드 블랙 트리 (1) | 2023.11.26 |
|---|---|
| 멀티웨이 탐색 트리 1 - m원 탐색 트리, B 트리, B*트리, B+ 트리 (2) | 2023.11.26 |
| 선택 트리, 숲, 이진 트리 개수 (2) | 2023.11.25 |
| 힙 - 개념, 우선순위 큐, 삭제 삽입 연산 (1) | 2023.11.24 |
| 스레드 트리, 개념, 구현, 연산 (순회 삽입 삭제) (0) | 2023.11.24 |



