1. 코드 변환기
디지털 시스템에서 교환할 정보에 대해 다른 코드를 사용한다면 코드 변환이 필요하다.
코드 변환기(code converter)
- 하나의 2진 코드를 다른 2진 코드로 바꾸어 주는 조합논리회로
- 다양한 코드 변환이 존재
BCD-3초과 코드 변환기 : BCD 코드를 3초과 코드로 변환해주는 변환회로
- BCD 코드라는 것은 2진수를 이용해서 0 ~ 9 까지 10진수 표현하는 것
- 3초과 코드라는 것은 입력코드에다가 3을 더해줘서 나오는 것
- 4비트를 이용하여 10진수 표현
- 따라서 4개의 입력과 4개의 출력이 필요
- 16가지 조합이 나오지만 총 10개의 조합만 사용하기 때문에 나머지 11 ~ 15는 무관조건으로 처리
설계 과정
1) 진리표 작성
2) 카노우 도표를 이용하여 간소화(부울함수 유도를 위해)
3) 출력 부울함수 유도
4) 논리회로도 작성
명세에 의해서 진리표를 작성한다.

3초과 코드 =>
입력이 0000이 들어갔으므로 0011이 나옴
카르노 도표를 통해서 부울함수를 구하면


이를 논리회로로 작성하면 다음과 같다.

BCD-9 변환기는 ?
-> BCD 코드가 입력되면 9의 보수값으로 변환
명세에 의해서 진리표를 구한다.
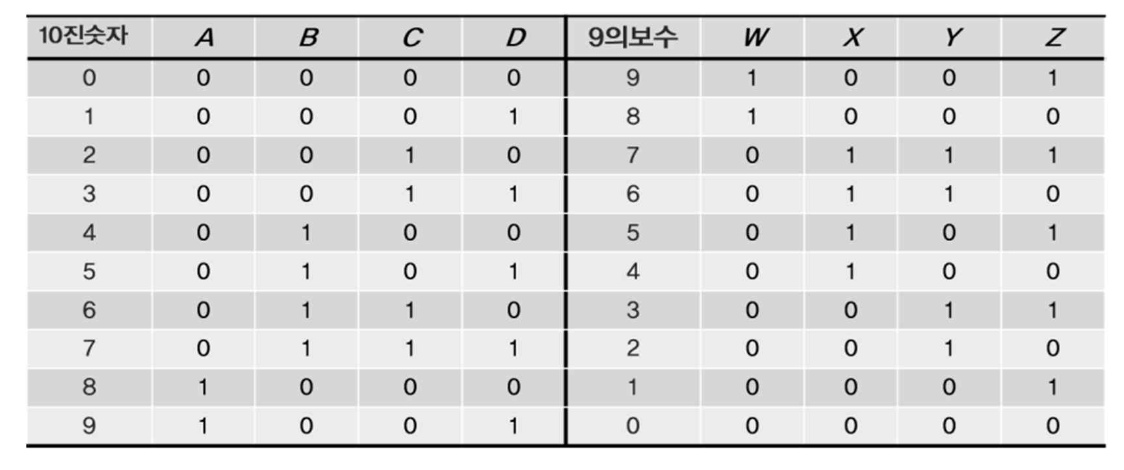
카르노 맵

출력 부울함수 유도 => 논리회로도 작성

2. 패리티 발생기/검사기
디지털 시스템에서 2진 정보를 주고 받을 때 잡음이나 회로상의 문제로 에러가 발생할 수 있다.
=> 정보의 손상
A 0010 => B 0011
잘못된 것인지 알 수가 없다.
이러한 에러 검출을 위해 전송되는 정보에 에러 검출용 비트를 추가해 전송한다.
=> 이때 사용되는 에러 검출용 비트를 패리티 비트라고 함.
발생기 : 송신단쪽
검사기: 수신단쪽
패리티 비트를 이용하는 방식
- 짝수 패리티검출(even parity check)방식: 2진 정보 속에 ‘1’의 개수가 패리티 비트를 포함하여 짝수가 되도록 패리티 비트를 부가하는 방식
- 홀수 패리티검출(odd parity check)방식(주로 사용한다): 2진 정보 속에 ‘1’의 개수가 패리티 비트를 포함하여 홀수가 되도록 패리티 비트를 부가하는 방식
패리티 비트 부가 방식 (BCD 코드의 경우)

보내려는 코드가 000이라고 하면 패리티 비트를 추가하면
짝수 = 00000 (1의 개수를 짝수개로 만들어주자)
홀수 = 00001 (1의 개수를 홀수개로 만들어주자)
일반적인 패리티 방식은 1개의 에러가 있을 때 검출가능하다.
그러나 동시에 2개의 에러가 있으면 검출 불가능
이러한 경우에 사용되는 방법이 이중 패리티 검출방식
이 방식은 코드를 한 묶음으로 하여, 그 묶음의 수직방향과 수평방향으로 패리티 비트를 부가한다.

수평과 수직으로 보낸다.
4번째 행의 코드 0110110 에 에러가 발생하여 코드 0111110 으로 된 경우

수직 방향으로도 체크를 해보면 1의 개수가 6개
이중으로 체크될때 어디가 잘못된지를 알 수 있게 된다.
이러한 패리티 검출을 위한 조합논리회로를 구현해보자.
- 발생기
- 검사기
발생기 설계 예시
-> 3비트 데이터 비트에 하나의 패리티 비트를 부가하는 홀수 패리티 발생기 설계
진리표 작성

1의 개수를 홀수개로 만들어주는 진리표를 완성
부울 함수를 유도

=> 홀수 함수의 형태
논리회로도 작성

검사기 설계 예시
- 패리티 발생기에 의해 만들어진 4비트 전송 정보에 대한 홀수 패리티를 검사
- 수신 쪽에서는 4비트를 받는다.
진리표 작성

카르노 도표

홀수 함수 형태로 나타난다.

패리티 비트 개념
발생 -> 수신 개념
회로가 필요하다를 이해하자.
3. BCD-세븐 세그먼트 표시기
세븐 세그먼트란?
- 7개의 막대를 이용해서 10진 숫자를 표시하는 장치
- 표시 장치 7개 a,b,c,d,e,f,g의 7개의 세그먼트로 구성

원하는 숫자를 표시한다는 것은 ?
0을 표현한다는 것은 g를 빼는 것

6을 표시한다는 것은 ?

b를 빼는 것
설계
-> BCD 코드의 네 개 입력과 세그먼트를 선택하는 7개의 출력을 갖는 표시기 설계
진리표 작성

0이라는 숫자 = > g를 제외하여 출력
8이라는 숫자 => 모든 것 출력
카르노 도표

각각 7개를 구함
논리회로도를 구하면 다음과 같다.

4. MSI를 이용한 조합논리회로
디지털 시스템에서
- 효과적인 조합논리회로를 설계하기 위해서는 주어진 함수를 실현하는데 필요한 게이트의 수를 최소화할 필요
- 이를 위해 집적회로(IC)를 사용
- 왜냐하면 패키지화된 IC의 내부 게이트를 이용하면 경제적인 설계 가능
이미 만들어진 MSI(Medium Scale Integrated circuits)장치를 이용하면 다양한 조합논리회로의 설계가 가능
MSI장치의 예
- 인코더, 디코더, 멀티플렉서, 디멀티플렉서
인코더
- 말그대로 부호화기
- 부호화되지 않은 입력을 받아서 부호로 바꿔 출력해줌
- e.g. A -> 65
인코더는 2n 개의 입력과 n 개의 출력을 갖고 있으며, 출력은 입력값에 대응하는 2진 코드를 생성한다.
8진을 2진으로 바꾸는 인코더 내부회로 설계
진리표

입력은 부호화되지 않은 수
출력은 부호화된 수


오직 하나의 입력만이 1이 될 수 있다고 가정
=> 특정 순간에 D0만 1, D1만 1
그런데 D3, D6가 동시에 1이 되면 A2, A1, A0은 111이 되어 2진수 3이나 6중 결정할 수 없다.
따라서 우선순위 부여
첨자가 큰 값에다가 우선순위를 준다.
우선순위 인코더: 우선순위를 부여하는 인코더
예를들어, 앞의 회로에서 D3, D6 가 동시에 1이 되면 세출력 A2, A1, A0 는
111 이 되어 2진수 3이나 6 중 어느 것으로도 결정할 수 없는 문제 발생

이를 해결하기 위해 입력의 첨자가 높을 수록 우선순위를 준다.
따라서D3 ,D6 가 동시에 1이 되어도 D6 가 D3 보다 우선순위가 높으므로 출력은 110 이 되어 6 이 된다.
참고자료: 디지털논리회로(김형근, 손진곤 공저, KNOU press 출판)
'CS > 디지털논리회로' 카테고리의 다른 글
| 순서논리회로의 분석, 상태표, 상태도 (0) | 2023.06.15 |
|---|---|
| 순서논리회로, 플립플롭, SR래치, D 플립플롭, JK 플립플롭, T 플립플롭, 플립플롭의 트리거링 (0) | 2023.06.15 |
| MSI를 이용한 조합논리회로, 디코더, 멀티플렉서, 디멀티플렉서 (1) | 2023.06.14 |
| 4변수 카르노 도표, 무관 조건, 기타 카르노 도표, NADN 게이트와 NOR 게이트를 이용한 논리회로 구현 (0) | 2023.06.14 |
| 조합논리회로의 분석과 설계, 기본 연산회로, 가산기, 감산기, 가감산기 (0) | 2023.06.14 |



