1. 조합논리회로
조합논리회로: 현재의 입력에 의해서만 출력이 결정되는 논리회로
순서논리회로: 조합논리회로에 저장요소를 추가한 회로 => 저장요소의 상태와 입력변수에 의해서 출력이 결정됨

조합논리회로의 분석
-> 주어진 논리회로에 대해서 입출력 관계를 구하는 것
-> 진리표나 부울함수를 구함으로써 분석이 이루어진다.
분석방법
- 부울함수 유도
- 진리표 작성
분석 방법 1 : 논리회로도에서 부울함수 유도
i) 각 게이트의 출력에 임의의 기호를 부여하고 각 게이트의 부울함수를 구한다.
ii) 단계 1에서 구해진 부울함수를 입력으로 하는 게이트의 출력에 다시 임의의 기호를 붙여 각 게이트에 대한 부울함수를 구한다.
iii) 회로의 최종 출력에 대한 부울함수를 얻을 때까지 단계 2를 반복한다.
예시

1) 중간게이트 OR의 출력을 T1 이라 하면
T1 = X + ~Y
2) 다른 중간 게이트 AND의 출력을 T2, T3 이라 하면
T2 = T1 · Z = (X + ~Y)Z
T3 = ~XY~Z
F = T2 + T3 = (X + ~Y)Z + ~XY~Z
분석 방법 2: 논리회로도에서 진리표 작성
i) 회로에서 입력변수의 개수를 정하고, n 개의 입력에 대해 표에 0 부터 2n-1 까지 모두 2n 개의 2진수 리스트를 작성
ii) 선택한 중간 출력 게이트에 임의의 기호를 붙인다.
iii) 입력변수로만 이루어진 출력 게이트에 대해 진리표 작성
iv) 모든 출력란을 작성할 때까지 중간 출력함수를 정리
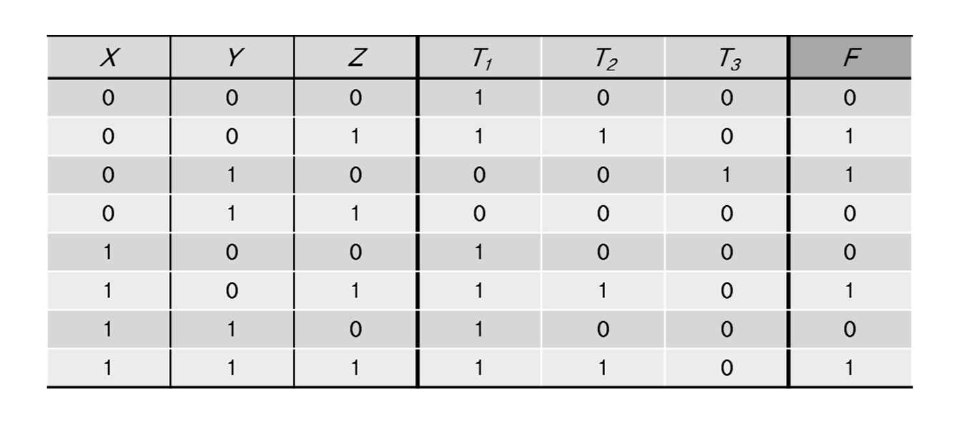
맨 왼쪽은 입력변수 3개에 대한 8개 조합
첫번째 경우 X=0, Y=0인 경우 Y가 NOT 게이트이니까 T1 = 1, T2는 T1과 Z의 AND 결합이므로 0 , 결과적으로 OR 조합인 F는 0
조합논리회로의 설계
-> 문제에 대한 설명으로부터 논리회로도나 논리회로를 작성할 수 있는 부울 함수를 구하는 과정
설계 과정
1 주어진 문제로 부터 입력변수와 출력변수의 개수를 결정하고, 각각을 적당한 기호로 표시하여 블럭도를 그린다.
2 입력변수와 출력변수와의 관계를 정의하는 진리표를 작성
3 각각의 출력을 입력변수의 함수로 나타내고 간소화한다.
4 논리회로도를 그린다.
즉 설계의 최종 결과는 회로도이다.
설계 예시)
3비트 2진수 중 10진수로서 홀수인 것은 그대로 출력에 통과시키고,
짝수인 것은 통과시키지 않는(즉, 출력을 000 으로 하는) 조합논리회로를 설계한다면 ?
(1) 입출력 관계를 블럭도로 나타낸다.

(2) 진리표를 작성 : 출력란에 입력중 홀수인 1,3,5,7은 입력값이 그대로, 그 외는 000으로 구성

3개의 입력으로 8개 조합을 표시하고
000이 왔을 때 출력이 뭐가 되느냐? 출력에 의해서 따져줌
홀수 인건 그대로 통과 = 001 = 1 이므로 그대로 나가게 함
즉, 주어진 요구사항에 따라 출력을 완성한다.
(3) 부울함수 유도 (간소화된)
간소화된 부울함수를 유도하기 위해 카르노 맵을 이용
F0 = m(1,3,5,7) => Z
F1 = m(3,7) => YZ
F2 = m(5,7) => XZ
(4) 논리회로도 작성

2. 기본연산회로
가감승제의 산술연산회로
- 가산기: 덧셈회로
- 감산기: 뺄셈회로
- 승산기: 곱셈회로
- 제산기: 나눗셈회로
조합논리회로에서는 가산기와 감산기만 다룬다. 승산기와 제산기는 플립플롭을 이용하므로 순서논리회로에서 다룬다.
가산기 (adder): 2진수의 덧셈을 수행하는 조합논리회로
올림수가 발생하는 경우 세비트 사이의 덧셈이 된다. 따라서 2비트, 3비트 나누어서 수행한다.
- 반가산기(HA: Half Adder): 두 비트의 덧셈을 수행
- 전가산기(FA: Full Adder): 세 비트의 덧셈을 수행
두 비트의 덧셈

캐리가 발생했냐 안했냐
-> 반가산기의 진리표
입력이 두개이므로 이진 조합 4가지에 대해 따져본다.

0 0 이 들어오면 0 0
0 1 이 들어오면 Summation만 1
1 0 이 들어와도 S만 1
1 1 이 들어오면 캐리가 발생한다.
카르노 도표로 구해보면

즉 이것으로 부울함수를 구하면

S = XOR 형식으로 표현될 수 있고
C = XY
반 가산기는 두 비트 사이의 덧셈만 수행하기 때문에 캐리가 발생하는 경우에 3비트 덧셈을 수행하지 못한다.
전가산기
=> 세 비트의 덧셈

진리표를 구하면 다음과 같다.

이를 부울함수를 유도해보면

다양한 논리회로도가 그려질 수 있다.
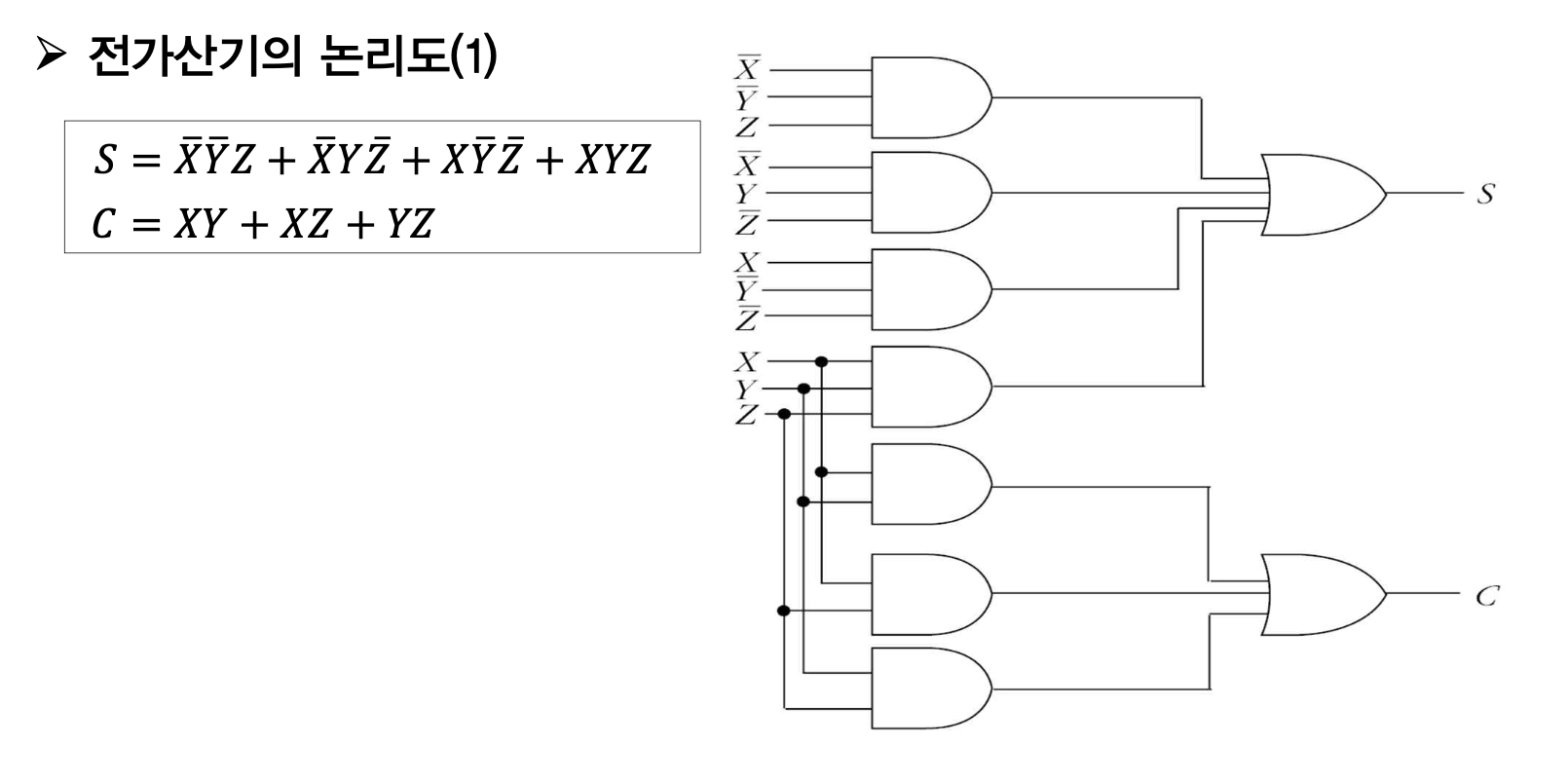

이때 반가산기를 떠올려보면 1개의 XOR과 AND 1개로 구성되어 있었다.
따라서 2개의 반가산기 (HA)가 모여져서 1개의 전 가산기가 구성되는 것을 알 수 있다.
가산기는 중요한 의미를 갖고 있는데, 컴퓨터에서 뺄셈이란 덧셈을 이용해서 하기 때문이다.
가산기는 크게 직렬가산기와 병렬가산기로 나눌 수 있다.
- 직렬방법: 회로구성비 저렴, 연산속도 늦음
- 병렬방법: 연산속도 빠름
병렬가산기를 알아보자.
- 전가산기를 연속 연결하여 구성
4비트 2진수를 더하는 병렬가산기를 구성하면 FA가 4개 구성되어 있다.
0000
+ 0010
----------
맨 마지막이 A0 B0

8비트라면 전가산기 8개를 이용한다.
감산기
-> 2진수의 뺄셈을 수행하는 조합논리회로
- 반가산기: 두 비트의 뺄셈을 수행
- 전가산기: 세 비트의 뺄셈을 수행
감산기에는 빌림수 B를 표현한다.
가산기에서와 마찬가지로 진리표를 구하고 부울함수를 구하면

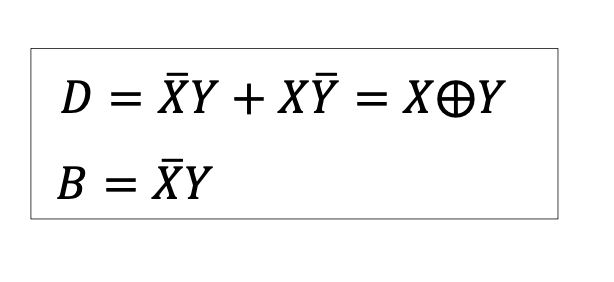
이러한 반감산기의 논리도를 구하면

그런데 이것은 반가산기의 논리도와 거의 같다.
반가산기

즉, NOT 게이트가 하나 있느냐 없느냐의 차이이다.
가산기에서는 캐리, 감산기에서는 borrow에 해당.
전감산기도 마찬가지로 논리도를 구하면

마찬가지로 NOT 게이트의 유무로 전가산기와 달라진다.
이론적으로 뺄셈은 가산기를 사용하되 NOT게이트를 이용해서 수행된다.
즉 하나의 회로에서 덧셈과 뺄셈을 할 수 있게 된다.
컴퓨터에 있어서 덧셈을 이용해서 뺄셈을 수행한다.
이것은 이론적으로 A - B는 ( A + B의 2의보수) 라는 공식으로써 진행된다.
그런데 2의 보수는 1의 보수를 취한 값의 최소 유효 비트에 1을 더하면 구해진다.
NOT 게이트로 (인버터)로 구해서 바꿔주고 거기다가 1만 더하면 2의 보수가 구해진다.
이러한 개념으로 감산회로를 만든다. 이때 FA를 통해서 만들고 B 쪽에다가 NOT 게이트만 추가해놓았다.

그렇다면 4비트 가감산기를 살펴보자.
=> 덧셈과 뺄셈을 가산기만으로 수행
덧셈도 하고 뺄셈도 하고자 하기 때문에 XOR 게이트를 추가하게 되고 FA로 구성

S가 0이냐 1이냐에 따라서 다른 연산을 수행한다.
=> S0를 보면 X와 Y의 XOR연산은 X~Y+~XY이므로
=> A0 + (B0~S +~B0S)
=> 이때 S가 0을 갖고 있는 거니까 ~S = 1
=> 결과적으로 A0 + B0만 남음
=> S0 = A0 + B0
즉 덧셈 수행을 한다.
만약에 S = 1이면
= A0 +(B0~S+~B0S) 이므로
= A0 + ~B0 + 1 이므로
=> 2의 보수가 구해져서 A0과 더해지므로
=> 결국 뺄셈을 수행하게 된다.
참고자료: 디지털논리회로(김형근, 손진곤 공저, KNOU press 출판)
'CS > 디지털논리회로' 카테고리의 다른 글
| MSI를 이용한 조합논리회로, 디코더, 멀티플렉서, 디멀티플렉서 (1) | 2023.06.14 |
|---|---|
| 4변수 카르노 도표, 무관 조건, 기타 카르노 도표, NADN 게이트와 NOR 게이트를 이용한 논리회로 구현 (0) | 2023.06.14 |
| 부울함수의 간소화, 카르노 도표 (0) | 2023.06.14 |
| 부울함수의 정규형 및 표준형, 최소항의 합, 최대항의 곱 (0) | 2023.06.14 |
| 논리연산, 논리 게이트, 부울 대수, 대수적 간소화 (0) | 2023.06.14 |



