1. 기본 계수 법칙
어떤 사건이 일어나는 방법이 전부 m가지 일때, 그 사건이 일어나는 '경우의 수'를 m가지라고 한다.
어떤 사건이 일어날 경우의 수를 세는 문제를 계수문제라고 한다. 계수문제 해결에는 다양한 법칙이 있으며, 그중 가장 기본적인 계수법칙으로는 곱셈법칙과 덧셈법칙이 있다. 이 두 법칙은 다른 모든 계수법칙의 기본이 된다.
(1) 곱의 법칙
두 사건 \( A \), \( B \)가 일어날 경우의 수가 각각 \( N(A) = m \), \( N(B) = n \)일 때, 사건 \( A \), \( B \)가 동시에 일어날 경우의 수는 \( m \times n \)이다. 즉,
\[ N_{A \cap B} = N_A \times N_B = m \times n \]
(2) 합의 법칙
두 사건 \( A \), \( B \)가 일어날 경우의 수가 각각 \( N(A) = m \), \( N(B) = n \)이고, \( A \cap B = \emptyset \)일 때, 사건 \( A \) 또는 \( B \)가 일어날 경우의 수는 \( m + n \)이다. 즉,
\[
N(A \cup B) = N(A) + N(B) = m + n
\]
📌 예시: 사용 가능한 숫자가 1부터 8까지이고, 자릿수는 4~6개인 비밀번호의 개수는 모두 몇 개인가?
4자리 짜리 비밀번호의 개수 = 𝟖𝟒 = 4,096
5자리 짜리 비밀번호의 개수 = 𝟖𝟓 = 32,768
6자리 짜리 비밀번호의 개수 = 𝟖𝟔 = 262,144
∴ 4,096 + 32,768 + 262,144 = 299,008
📌 예시: 32bit 인터넷 주소(IPv4)는 A, B, C의 클래스로 구분된다. A 클래스는 첫 번째 비트가 0으로 시작되는 인터넷 주소를 가지고 있으며, B 클래스는 앞선 2비트가 10으로 시작되는 인터넷 주소를 가지고 있고, C 클래스는 앞선 3비트가 110으로 시작되는 인터넷 주소를 가지고 있다. 각각의 클래스는 네트워크와 호스트 부분으로 다음 그림과 같이 구분되어 있을 때, 3개의 클래스틀 통해 구분할 수 있는 최대 네트워크의 개수를 구하면 몇 개인가?
✘ 풀이:
클래스 A의 네트워크 개수는 다음과 같다.
\[
2^7 = 128
\]
클래스 B의 네트워크 개수는 다음과 같다.
\[
2^{14} = 16,384
\]
클래스 C의 네트워크 개수는 다음과 같다.
\[
2^{21} = 2,097,152
\]
따라서
\[
128 + 16,384 + 2,097,152 = 2,113,664
\]
합집합의 크기
다음은 집합 \(A\), \(B\), \(C\)가 유한집합일 때 성립하는 식들이다.
\[
A \cup B = |A| + |B| - |A \cap B|
\]
\[
A \cup B \cup C = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|
\]
집합 \(A\)와 \(B\)가 유한집합이면서 서로소일 때, 다음이 성립한다.
\[
A \cup B = |A| + |B|
\]
여기서, 서로소(disjoint) 집합이란 \(A \cap B = \emptyset\) 즉, 교집합이 공집합인 경우.
📌 예제: 8비트 이진수 중 비트열 ‘100’으로 시작하거나 비트열 ‘100’으로 끝나는 이진수의 개수를 구하시오.
✘ 풀이:
'100'으로 시작하는 이진수의 개수는 다음과 같다.
\[
2^5 = 32
\]
'100'으로 끝나는 이진수의 개수는 다음과 같다.
\[
2^5 = 32
\]
'100'으로 시작해서 '100'으로 끝나는 이진수의 개수는 다음과 같다.
\[
2^2 = 4
\]
따라서, '100'으로 시작하거나 '100'으로 끝나는 이진수의 개수는 다음과 같다.
\[
32 + 32 - 4 = 60
\]
2. 순열
객체의 집합에서 순서를 고려하여 객체를 배열하는 것을 순열(permutation)이라 한다.
📌 예제: A, B, C, D, E, F, G, H 라는 8개의 문자를 모두 한 번씩만 이용하여 만들 수 있는 단어는 몇 가지인가?
✘ 풀이: 중복되는 문자가 없는 8개의 문자이므로 이를 이용하여 만들 수 있는 8개 문자의 단어 개수는 8! = 40,320이다.
(1) 순열
𝟎 <= r <= n을 만족하는 정수 \( n \), \( r \)에 대하여, \( n \)개의 원소를 갖는 집합에서 순서를 고려해서 \( r \)개의 원소를 뽑는 경우의 수는
\[
P(n, r) = n(n-1)(n-2) \cdots (n-r+1)
\]
또는
\[
P(n, r) = \frac{n!}{(n-r)!}
\]
이다.
📌 예제: 1부터 5까지의 숫자를 한 번씩만 사용하여 만들 수 있는 3자리 수는 모두 몇 가지인가?
✘ 풀이:
1. 사용 가능한 숫자는 1, 2, 3, 4, 5이다.
2. 각 숫자는 한 번만 사용할 수 있다.
3. 3자리 수를 만들어야 한다.
3자리 수를 만들기 위해 숫자 3개를 선택하고, 그 숫자들을 배열하는 경우의 수를 계산해야 한다.
먼저, 5개의 숫자 중에서 3개의 숫자를 선택하는 경우의 수는 다음과 같다.
\[ P(5,3) = \frac{5!}{(5-3)!} = \frac{5!}{2!} = 5 \times 4 \times 3 = 60 \]
따라서, 1부터 5까지의 숫자를 한 번씩만 사용하여 만들 수 있는 3자리 수는 총 60가지.
📌 예제: 10명의 학생 중에서 3명을 선발해서 과제 발표를 시키려고 한다. 한 명의 학생은 한 번만 발표할 수 있다고 할 경우, 발표 순서는 모두 몇가지인가?
✘ 풀이: 10명 중 3명의 발표 순서는 \[ P(10, 3) = \frac{10!}{(10-3)!} = \frac{10!}{7!} \] = 720
중복집합에서의 순열
중복된 원소를 허용하는 중복집합의 크기가 \( n \)이고 그 중에서 중복된 원소의 개수가 각각 \( p \)개, \( q \)개, ⋯ , \( r \)개가 있을 때, \( n \)개 모두를 일렬로 배열하는 경우의 수는 다음과 같다.
\[
\frac{n!}{p! q! \cdots r!}
\]
📌 예제: A, A, A, B, B, B, C, C, C, C 라는 문자 10개를 모두 한 줄로 나열하여 만들 수 있는 단어 개수는 모두 몇가지 인가?
✘ 풀이: 10개의 문자를 나열하는 경우의 수는 10!이다. 사용할 수 있는 무자 중에는 A가 3개, B가 3개, C가 4개이다. 따라서 한 줄로 나열하여 만들 수 있는 단어 개수는
\[
\frac{10!}{3! \cdot 3! \cdot 4!}
\]
= 4,200 가지
📌 예제: 노드 A에서 노드 B까지의 최단 경로의 방법은?
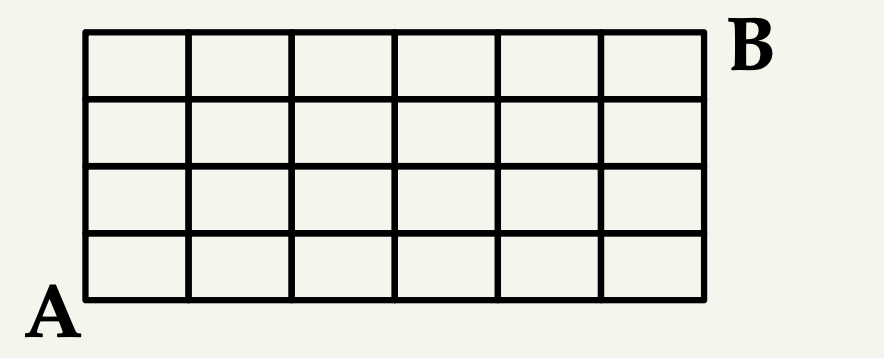
✘ 풀이:
오른쪽 이동을 \( r \)이라고 하고, 위로 이동을 \( u \)라고 한다.
A에서 B까지 6개의 \( r \)과 4개의 \( u \)가 필요하다.
10개의 변을 지나 A에서 B까지 이동하는 방법의 수는 다음과 같다.
\[
\binom{10}{6} = \frac{10!}{6! \times 4!}
\]
중복순열
\( n \)개의 원소를 갖는 집합에서 **중복을 허용**하고 **순서를 고려해서** \( r \)개 원소를 뽑는 경우의 수는
\[
n \Pi r = n^r
\]
📌 예제: 친구와 가위바위보 게임을 네 번 하기로 했다. 내가 네 번 게임할 동안 낼 수 있는 손 모양의 경우의 수는 얼마인가?
✘ 풀이: 한 번의 게임에서 낼 수 있는 손 모양의 종류는 세 가지이고, 중복이 허용되므로 총 경우의 수는 3^4 = 81
📌 예제: 1부터 9까지의 숫자를 이용해서 만들 수 있는 4자리의 개수는?
✘ 풀이: 중복이 허용되므로 경우의 수는 9^4 = 6,561
📌 예제: S, M, A, R, T의 5개 문자 중 3개를 이용해서 (중복을 허용함) 만들 수 있는 단어는 모두 몇가지인가?
✘ 풀이:
$$
5^3 = 125
$$
원순열
n개의 원소를 갖는 집합의 모든 원소들을 원형으로 나열하는 경우의 수는 다음과 같다.
\[
\frac{n!}{n} = \frac{n (n-1)!}{n} = (n-1)!
\]
즉, n개의 원소를 원형으로 나열하는 경우의 수는 \((n-1)!\)
📌 예제: A, B, C, D 4명이 하나의 원탁에 앉으려고 한다. A와 B가 서로 마주 보고 앉을 수 있는 경우의 수는?
✘ 풀이: A와 B가 서로 마주 보고 앉게 되므로 두 명 중 한 명의 자리가 정해지면 다른 한 명의 위치는 고정될 수 밖에 없다. 즉, 4명 중에서 B를 제외한 3명을 원탁에 앉힌 다음, 제외되었던 B를 A 앞에 앉히면 된다. 따라서 A와 B가 마주보고 앉을 경우의 수는 (3-1)! = 2! = 2
3. 조합
(1) 조합
0 ≤ \( r \) ≤ \( n \)을 만족하는 정수 \( r \)과 \( n \)에 대하여,
\( n \)개의 원소를 갖는 집합에서 \( r \)개의 원소를 순서 없이 뽑는 경우의 수는 \( C_{n,r} \)이다.
\[
C_{n,r} = \frac{P(n,r)}{r!}
\]
또는
\[
C_{n,r} = \frac{n!}{r!(n-r)!}
\]
📌 예제: 8개의 버튼으로 된 자물쇠에서 4개의 버튼을 눌러 비밀번호를 만들려고 한다면 몇 가지 경우인가?
✘ 풀이: 8개 버튼 중 순서를 고려하지 않고 4개를 선택하는 것이므로 조합을 이용한다.
\[ \binom{8}{4} = \frac{8!}{4!(8-4)!} = \frac{8!}{4!4!} \]
\[ 8! = 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \]
\[ 4! = 4 \times 3 \times 2 \times 1 \]
이를 대입하여 계산하면,
\[ \binom{8}{4} = \frac{8 \times 7 \times 6 \times 5 \times 4!}{4! \times 4!} = \frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} = \frac{1680}{24} = 70 \]
따라서, 8개의 버튼 중에서 4개의 버튼을 눌러 비밀번호를 만드는 경우의 수는 70가지이다.
📌 예제: 12명의 타자가 있는 야구팀이 있다. 이 중에서 9명의 선발 타자를 뽑는 방법은 모두 몇 가지인가?
✘ 풀이: 12명 중 9명을 선택하는 것과 12명 중 3명을 선택하는 것은 경우의 수가 같다.
따라서, 이는 다음과 같이 계산할 수 있다.
\[
\binom{12}{9} = \binom{12}{3}
\]
이를 계산하면,
\[
\binom{12}{3} = \frac{12!}{3!(12-3)!} = \frac{12 \times 11 \times 10}{3 \times 2 \times 1} = 220
\]
따라서, 12명 중 9명을 선택하는 방법은 220가지이다.
📌 예제: 집합 {a, b, c, d, e}에서 3개의 원소를 가지는 부분집합은 몇 개인가?
✘ 풀이: 집합에서는 원소의 순서를 고려하지 않아도 되므로 조합을 이용한다.
주어진 예제에서, \( n = 5 \)이고 \( r = 3 \)이므로, 조합의 수를 구하면 다음과 같다:
\[
\binom{5}{3} = \frac{5!}{3!(5-3)!} = \frac{5 \times 4 \times 3!}{3! \times 2 \times 1} = \frac{5 \times 4}{2 \times 1} = 10
\]
따라서 집합 \(\{a, b, c, d, e\}\)에서 3개의 원소를 가지는 부분집합의 수는 총 10개이다.
(2) 이항 정리
이항 정리(binomial theorem)은 임의의 실수 \(x, y\)와 음이 아닌 정수 \(n\)이 주어졌을 때 다음과 같이 나타낼 수 있다.
\[
(x + y)^n = \sum_{k=0}^{n} \binom{n}{k} x^{n-k} y^k
\]
이는 다음과 같은 항들의 합으로 표현된다.
\[
\binom{n}{0} x^n y^0 + \binom{n}{1} x^{n-1} y^1 + \cdots + \binom{n}{n} x^0 y^n
\]
📌 예제: \((x + y)^{12}\)의 전개식에서 \(x^4 y^8\)의 계수를 구하시오.
✘ 풀이: 이항 정리에 의해서 \(x^4 y^8\)의 계수는 다음과 같다.
\[
\binom{12}{8} = \binom{12}{4}
\]
이를 계산하면,
\[
\binom{12}{4} = \frac{12 \times 11 \times 10 \times 9}{4 \times 3 \times 2 \times 1} = 495
\]
따라서 \(x^4 y^8\)의 계수는 495이다.
4. 이산확률
표본공간과 사건
어떤 실험을 하였을 때, 가능한 모든 결과 중에서 반드시 하나의 결과만 나타난다고 하자.
실험의 모든 결과의 집합을 표본공간(sample space)이라 하며,
표본공간의 부분집합을 사건(event)이라고 한다.
수학적 확률
표본공간 \( S \)가 유한하며 각 사건이 발생할 가능성이 모두 동일하다고 가정할 때, 사건 \( E \subset S \)가 발생할 확률은 다음과 같다.
이때, \(\forall s \in S\), \(0 \leq P_s \leq 1\), \(P(\emptyset) = 0\), \(\sum_{s \in S} P_s = 1\). 또한, \(\forall A, B \in S\), 만일 \(A \cap B = \emptyset\)이면,
수학적 확률은 다음과 같다.
\[ P(E) = \frac{|E|}{|S|} \]
또한,
\[ P(A \cup B) = P(A) + P(B) \]
여기서 \(E\)는 사건, \(A\)와 \(B\)는 서로소 사건이다.
📌 예제: 주사위를 두 번 던졌을 때, 숫자의 합이 3일 확률을 구하시오.
✘ 풀이:
주사위를 두 번 던졌을 때 표본공간의 크기는 \(6^2 = 36\)이다. 숫자의 합이 3인 사건은 다음과 같다: \((1, 2)\)와 \((2, 1)\) 두 가지 경우가 있다. 따라서, 구하는 확률은 \(\frac{2}{36} = \frac{1}{18}\)이다.
조건부 확률
표본공간 \( S \) 에 두 사건 \( A \), \( B \) 가 있고, \( P(B) > 0 \) 이라고 하자. 사건 \( B \) 가 발생했다는 가정하에 사건 \( A \) 가 발생할 확률을 조건부 확률(conditional probability) \( P(A|B) \) 라고 한다.
조건부 확률 \( P(A|B) \) 는 다음과 같이 정의된다:
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
여기서 \( P(A \cap B) \) 는 사건 \( A \) 와 \( B \) 가 동시에 발생할 확률이다.
📌 예제:
전체 중고차 중 70%가 네비게이션이 있고, 40%는 블랙박스가 있다고 하자. 전체 중고차 중 90%가 둘 중 하나는 가지고 있다고 할 때, 네비게이션이 없는 중고차 중 블랙박스도 없을 확률을 구하시오.
✘ 풀이:
네비게이션이 없을 확률을 \( P(B) \)로 나타내면 다음과 같다:
\[ P(B) = 1 - 0.7 = 0.3 \]
블랙박스가 없을 확률을 \( P(A) \)로 나타내면 다음과 같다:
\[ P(A) = 1 - 0.4 = 0.6 \]
둘 다 없을 확률은 \( P(A \cap B) \)로 나타내면 다음과 같다:
\[ P(A \cap B) = 1 - 0.9 = 0.1 \]
네비게이션이 없는 중고차 중 블랙박스도 없을 확률은 다음과 같다:
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{0.1}{0.3} = 0.333\ldots \]
따라서, 네비게이션이 없는 중고차 중 블랙박스도 없을 확률은 약 \( 33.3\% \)이다.
5. 점화식
점화식이란 수열의 항 사이에서 성립하는 관계식이다. 즉, 수열 \( a_1, a_2, \cdots, a_{n-1}, a_n, \cdots \)에서 항 \( a_n \)을 그전의 항들 \( (a_1, a_2, \cdots, a_{n-1}) \)의 함수로 나타낼 경우, 그 함수를 수열에 관한 점화식이라고 부른다. 주어진 수열에 관한 점화식을 푼다는 것은 수열의 일반항인 \( a_n \)을 \( n \)에 관한 식으로 나타내는 것이다.
📌 예제: 수열 1, 4, 7, 10, 13, ⋯의 점화식을 구하고 점화식의 해를 구하시오.
✘ 풀이:
시작항은 1이고 각 항의 차이는 3이므로 수열의 점화식은 다음과 같다.
$$
a_0 = 1, \quad a_n = a_{n-1} + 3
$$
점화식의 해를 구하면 다음과 같다.
$$
a_n = a_{n-1} + 3 = a_{n-2} + 3 \times 2 = a_{n-3} + 3 \times 3 = \cdots
$$
이를 일반화하면,
$$
a_n = a_{n-n} + 3 \times n = a_0 + 3n
$$
따라서,
$$
a_n = 1 + 3n
$$
6. 비둘기집 원리
\(k\)개의 상자에 \(N\)개의 물체를 넣게 되면, 적어도 하나의 상자는 \( \left\lceil \frac{N}{k} \right\rceil \) 개 이상의 물체를 포함하게 된다.
\[
k \text{개의 상자에 } N \text{개의 물체를 넣을 때,}
\]
\[
\exists \, i \in \{1, 2, \ldots, k\} \text{ such that } n_i \geq \left\lceil \frac{N}{k} \right\rceil
\]
여기서, \(n_i\)는 \(i\)번째 상자에 있는 물체의 개수이다. \( \left\lceil \cdot \right\rceil \)는 올림 기호로, 해당 값을 올림한 정수값을 의미한다.
따라서, \(N\)개의 물체를 \(k\)개의 상자에 분배할 때, 적어도 하나의 상자는 \( \left\lceil \frac{N}{k} \right\rceil \)개 이상의 물체를 가지게 됨을 알 수 있다.
예를 들어, 0에서 9 사이의 숫자가 쓰여 있는 31개의 공에는 4번 이상 나오는 숫자가 반드시 존재한다. 31개의 물체를 10개의 상자에 놓을 경우 4개 이상 물체가 들어간 상자가 반드시 존재하기 때문이다.
📌 예제: 컴퓨터실에는 10대의 서버와 15대의 단말기가 있고, 서버와 단말기는 케이블로 직접 연결될 수 있다. 각각의 단말기는 연결된 하나의 서버에만 접속될 수 있다. 15대의 단말기 앞에 무작위로 10명이 앉는다고 할 때, 10명 앞에 놓여진 단말기가 전부 서버에 접속되는 것을 보장하고자 한다. 다음 물음에 답하시오.
1) 서버와 단말기를 연결하기 위해 필요한 최소한의 연결선은 몇 개인가?
2) 서버와 단말기 사이에 연결선을 어떻게 설계해야 하는가?
✘ 풀이:
1) 먼저, 모든 서버가 모든 단말기에 연결되려면 \(10 \times 15 = 150\)개의 연결선이 필요하다. 그러나 이렇게 많은 연결선을 사용하는 대신, 더 적은 수의 연결선으로 무작위로 선택된 10대의 단말기가 각각의 서버에 접속되도록 설계할 수 있다.
이 문제를 해결하려면 각 서버가 최소한 몇 대의 단말기와 연결되어 있어야 하는지를 생각해보자. 15대의 단말기 중 10대의 단말기를 무작위로 선택한다고 가정한다.
만약 한 서버가 5대 이하의 단말기와만 연결되어 있다면, 그 서버는 10명이 접속할 수 있는 최소한의 요건을 충족시키지 못한다. 왜냐하면 남은 9대의 서버로는 무작위로 선택된 10대의 단말기를 모두 접속시킬 수 없기 때문이다.
따라서 각 서버는 최소한 6대의 단말기와 연결되어 있어야 한다. 이 경우, 10대의 서버가 각각 6대의 단말기와 연결되어 있다면 \(10 \times 6 = 60\)개의 연결선이 필요하게 된다.
결국, 10명의 사용자가 앉아있는 10대의 단말기가 모두 서버에 접속되기 위해서는 최소한 60개의 연결선이 필요하다.
2)
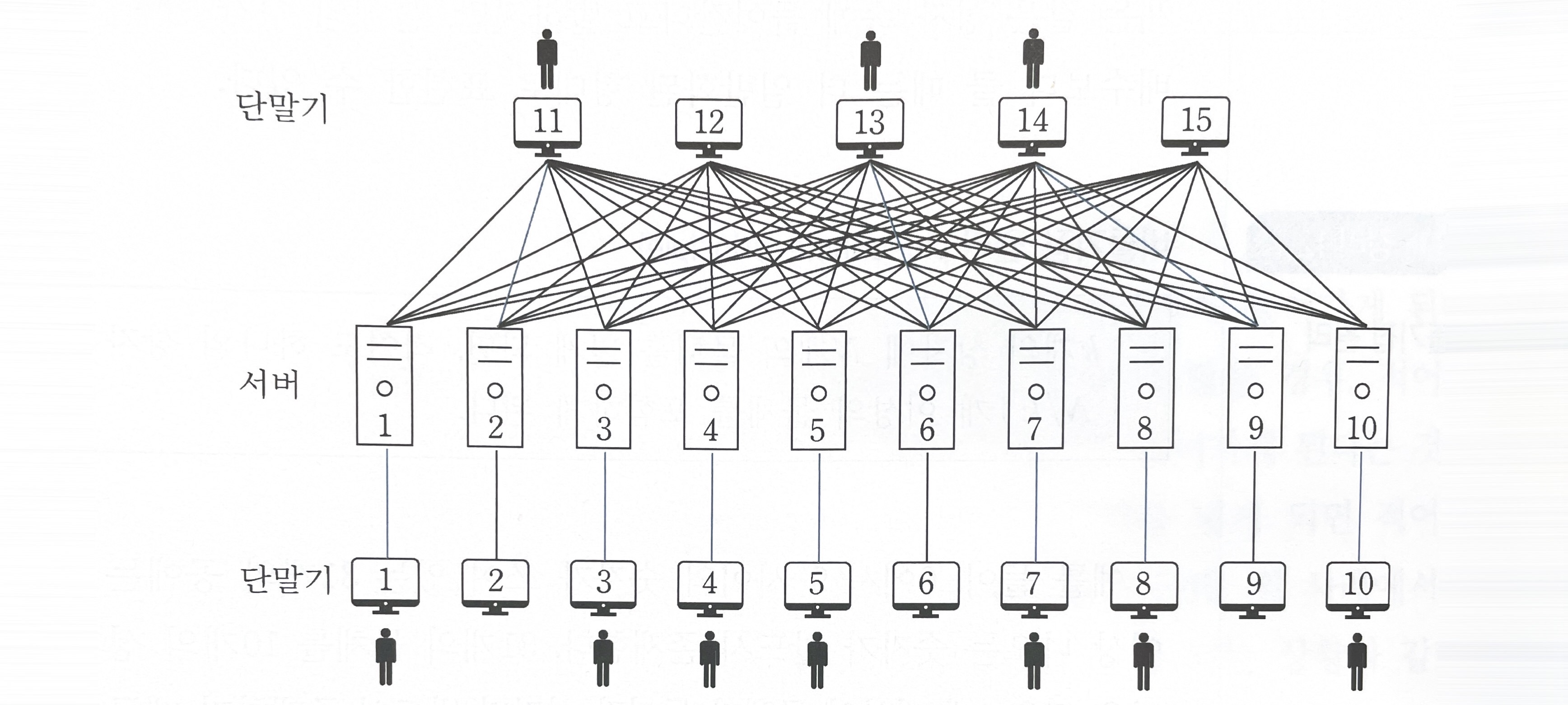
참고자료: 이산수학 | 손진곤 (지은이) 한국방송통신대학교출판문화원
'CS > 이산수학' 카테고리의 다른 글
| 이산수학 - 정수론, 나눗셈, 베주의 항등식, 유클리드 호제법, 나머지 연산, 소수와 소인수 분해, RSA 암호 (0) | 2024.05.15 |
|---|---|
| 이산수학 - 그래프, 트레일, 경로, 이분 그래프, 완전 이분 그래프, 정규 그래프, 오일러 투어, 해밀턴 경로 (0) | 2024.05.15 |
| 이산수학 - 함수, 함수의 상등, 전사함수, 단사함수, 합성함수, 계승함수, 바닥함수, 천장함수, 나머지 함수 (0) | 2024.05.15 |
| 이산수학 - 관계, 관계의 표현, 관계의 성질, 관계의 종류, 반사적, 대칭적, 추이적, 동치관계 (0) | 2024.05.15 |
| 이산수학 - 행렬: 행렬의 연산, 종류, 정방행렬, 단위행렬, 역대칭행렬, 삼각행렬, 역행렬, 부울행렬 (0) | 2024.05.15 |



