1. 기본사항
관계란 객체들 간의 연관성을 포현하는 구조이다.
이산수학에서 관계는 주로 두 집합에 속하는 서로 다른 두 원소 사이의 연관성을 표현하는 데 사용된다.
두 집합 X와 Y에 대하여 곱집합 X x Y의 부분집합 R을 X에서 Y로의 관계라고 말한다.
집합 \(A\)와 \(B\)의 곱집합(Cartesian Product) \(A \times B\)는 \(A\)의 원소와 \(B\)의 원소의 모든 순서쌍(ordered pair)들의 집합을 의미합니다. 즉,
\[ A \times B = \{ (a, b) \mid a \in A, b \in B \} \]
집합 \( X \)에서 집합 \( Y \)로의 (이항)관계 \( R \)은 \( X \times Y \)의 부분집합이다.
- 이항관계 \( R \)에 대해, \( (x, y) \in R \)이면 \( x \)는 \( y \)와 \( R \)의 관계가 있다.
- 이를 \( xRy \)로 표기할 수 있다.
- 만약 \( X = Y \)이면, \( R \)을 \( X \)에서의 관계라고 한다.
\[ R \subseteq X \times Y \]
\( R \)이 이항관계라면, 다음이 성립한다/
\[ (x, y) \in R \implies xRy \]
그리고, 만약 \( X = Y \)이면, \( R \)은 \( X \)에서의 관계이다.
📌 예시
집합 \( X = \{1, 2\} \), 집합 \( Y = \{a, b\} \)에서 관계 \( R \)을 정의해보자. \( R \subseteq X \times Y \)이고, 다음과 같은 원소를 가질 수 있다.
\[ R = \{(1, a), (2, b)\} \]
이 경우, \( (1, a) \in R \)이므로 \( 1Ra \), \( (2, b) \in R \)이므로 \( 2Rb \)라고 할 수 있다.
또한, 집합 \( X = \{1, 2\} \)에서의 관계 \( R \)을 정의해보자. 이 경우, \( X = Y \)이므로 \( R \subseteq X \times X \)이다. 다음과 같은 원소를 가질 수 있다.
\[ R = \{(1, 1), (2, 2), (1, 2)\} \]
이 경우, \( (1, 1) \in R \)이므로 \( 1R1 \), \( (2, 2) \in R \)이므로 \( 2R2 \), \( (1, 2) \in R \)이므로 \( 1R2 \)라고 할 수 있다.
\[
\begin{align*}
R &\subseteq X \times Y \\
(x, y) &\in R \implies xRy
\end{align*}
\]
2. 관계의 표현
1) 화살표 도표
𝒙 ∈ 𝑿, 𝒚 ∈ 𝒀, (𝒙, 𝒚) ∈ 𝑹
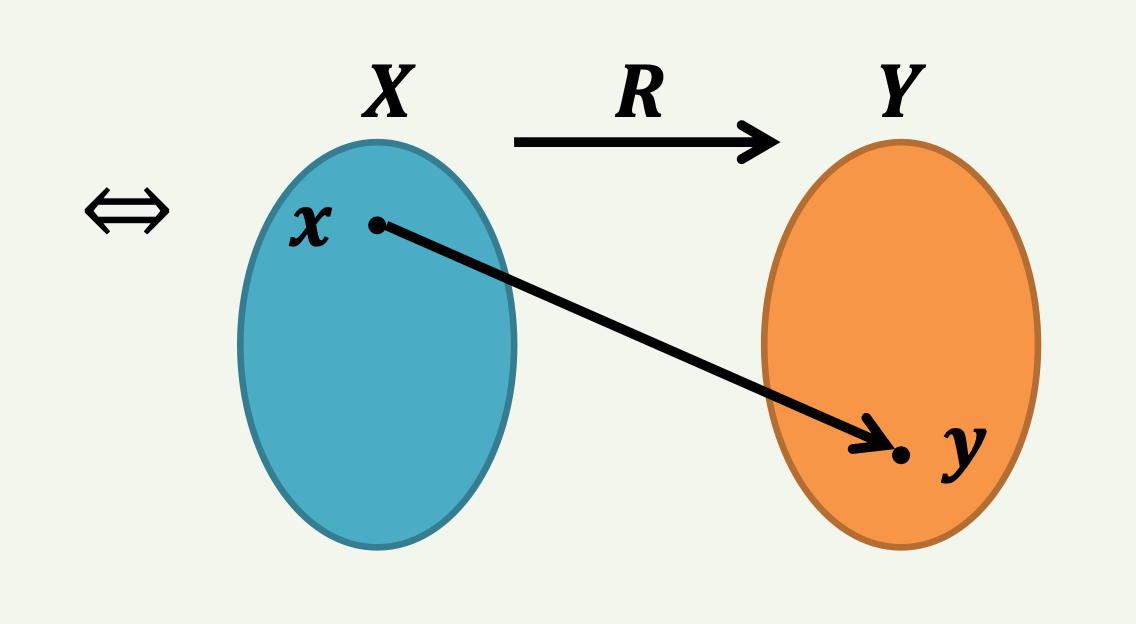
📌 예시:
\[
A = \{ 1, 2, 3, 4 \}, \quad B = \{ -1, 0, 1, 2 \}
\]
(1) \( x, y \in A \times B \) 에 대해, \( x, y \in \mathbb{R} \) 이기 위한 필요충분조건은 \( y > x \)

2) 방향 그래프
그래프 : 점[꼭지점](vertex)과 선[변](edge)으로 이루어진 도형
-> G = (V, E)
𝒙,𝒚∈𝑿, (𝒙,𝒚)∈𝑹

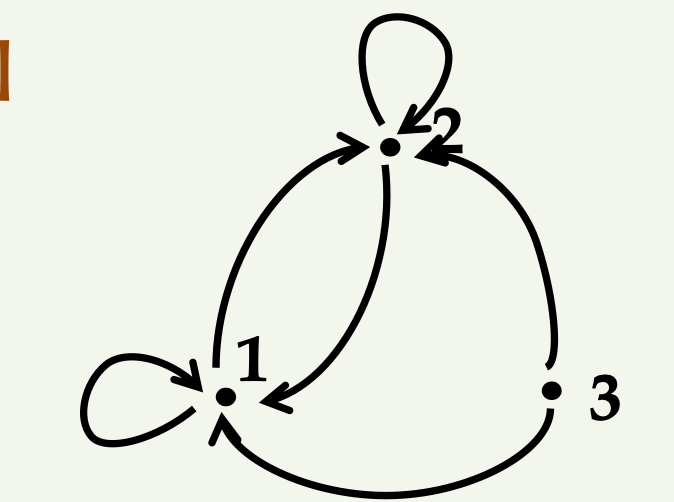
📌 예시: 관계 T를 방향 그래프로 나타내시오.
A = { 1, 2, 3}
T = { (1,1), (1,2), (2,2), (3,1), (3,2)}
3) 부울행렬
\[ X = \{ x_1, x_2, \ldots, x_m \}, \quad (x_i, y_j) \in R \]
\[ Y = \{ y_1, y_2, \ldots, y_n \} \]
이에 따라 \( m \times n \) 부울행렬 \( M_R \)는 다음과 같다.
\[ M_R = [a_{ij}] \]
여기서,
\[ a_{ij} =
\begin{cases}
1 & \text{if } (x_i, y_j) \in R \\
0 & \text{if } (x_i, y_j) \notin R
\end{cases}
\]
📌 예시:
관계 T를 부울행렬로 나타내시오.
𝑨= {𝟏,𝟐,𝟑}
𝑻={(𝟏,𝟏), (𝟏,𝟐), (𝟐,𝟏), (𝟐,𝟐), (𝟑,𝟏), (𝟑,𝟐)}
\[ M_T =
\begin{pmatrix}
1 & 1 & 0 \\
1 & 1 & 0 \\
1 & 1 & 0
\end{pmatrix}
\]
3. 관계의 성질
(1) 성질의 종류
집합 \(A\)에서의 관계 \(R\)이
1. 반사적 (reflexive)
\[
\forall a \in A, (a, a) \in R
\]
2. 대칭적 (symmetric)
\[
\forall a, b \in A, (a, b) \in R \Rightarrow (b, a) \in R
\]
3. 추이적 (transitive)
\[
\forall a, b, c \in A, (a, b) \in R \land (b, c) \in R \Rightarrow (a, c) \in R
\]
(2) 관계의 성질과 부울행렬
📌 예시1:
𝑨= {𝟏,𝟐,𝟑,𝟒} 𝑨에서의 관계 𝑹, 𝑺, 𝑻의 성질을 설명하시오.
(1) 𝑹 = { (𝟏, 𝟏), (𝟐, 𝟐), (𝟑, 𝟑) }
(2) 𝑺 = {(𝟏,𝟏), (𝟏,𝟐), (𝟏,𝟑), (𝟏,𝟒), (𝟐,𝟑), (𝟐,𝟒), (𝟑,𝟒)}
(3) 𝑻 = {(𝟏,𝟒), (𝟐,𝟑), (𝟑,𝟐), (𝟒,𝟏)}
1)
\[
R = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 \\
\end{pmatrix}
\]
- 반사적이지 않음
- 대칭적임
- 추이적임
2)
\[
S = \begin{pmatrix}
1 & 1 & 1 & 1 \\
0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
\end{pmatrix}
\]
- 반사적이지 않음
- 대칭적이지 않음
- 추이적임
3)
\[
T = \begin{pmatrix}
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
\end{pmatrix}
\]
- 반사적이지 않음
- 대칭적임
- 추이적이지 않음
4. 관계의 종류
(1) 역관계
집합 X에서 집합 Y로의 관계 R이 있을 때, 관계를 구성하는 각 순서쌍의 원소 순서를 바꾸면 Y에서 X로의 관계가 되며, 이를 역관계라고 한다.
\( X \), \( Y \) : 집합
\( R \) : \( X \)에서 \( Y \)로의 관계
\( R^{-1} \) : \( R \)의 역관계 (inverse relation)
\( R^{-1} = \{ (y, x) \mid (x, y) \in R \} \subseteq Y \times X \)

📌 예시: 𝑹과 𝑺의 역관계 구하기
\(A = \{1, 2, 3, 4\}\), \(B = \{0, 1, 2, 3\}\)
\(R = \{(x, y) \mid y = x - 1, x \in A, y \in B\}\)
\(S = \{(1, 2), (2, 3), (3, 0), (4, 1)\}\)
[풀이]
1. \(R^{-1}\):
\(R^{-1} = \{(y, x) \mid y = x - 1, x \in A, y \in B\}\)
\[
R^{-1} = \{(0, 1), (1, 2), (2, 3), (3, 4)\}
\]
2. \(S^{-1}\):
\(S^{-1} = \{(y, x) \mid (x, y) \in S\}\)
\[
S^{-1} = \{(2, 1), (3, 2), (0, 3), (1, 4)\}
\]
(2) 합성관계
\(A, B, C\): 집합
\(R\): \(A\)에서 \(B\)로의 관계
\(S\): \(B\)에서 \(C\)로의 관계
\(R\)과 \(S\)의 합성관계 (composition relation) \(S \circ R\):
\[ S \circ R = \{ (a, c) \mid a \in A, b \in B, c \in C, (a, b) \in R, (b, c) \in S \} \]
따라서,
\[ S \circ R \subseteq A \times C \]
(즉, \(A\)에서 \(C\)로의 관계)
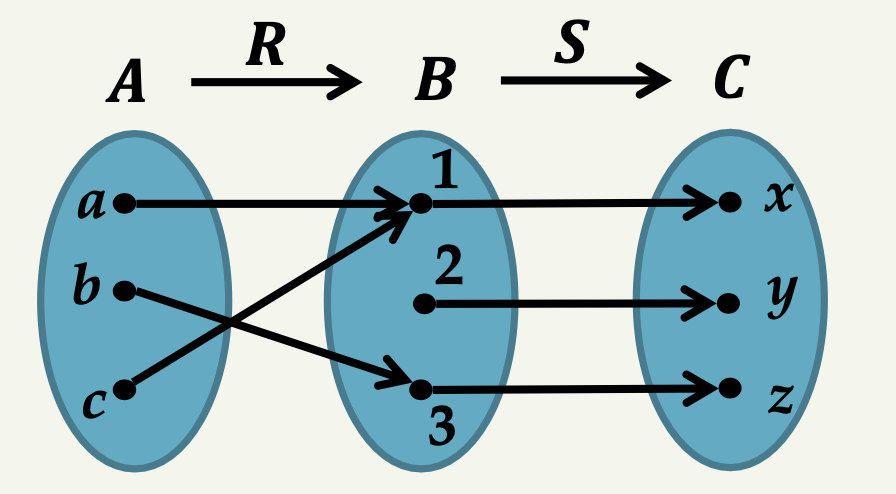
📌 예시: \( S \circ R \) 구하기
집합 \( A \) = \(\{a, b, c\}\), 집합 \( B \) = \(\{1, 2, 3\}\), 집합 \( C \) = \(\{x, y, z\}\)
관계 \( R \) = \(\{ (a, 1), (b, 3), (c, 1) \}\)
관계 \( S \) = \(\{ (1, x), (2, y), (3, z) \}\)
풀이:
\( S \circ R \) = \(\{ (a, x), (b, z), (c, x) \}\)
수식으로 정리하면 다음과 같다:
\[
A = \{a, b, c\}
\]
\[
B = \{1, 2, 3\}
\]
\[
C = \{x, y, z\}
\]
\[
R = \{ (a, 1), (b, 3), (c, 1) \}
\]
\[
S = \{ (1, x), (2, y), (3, z) \}
\]
\[
S \circ R = \{ (a, x), (b, z), (c, x) \}
\]
(3) 동치관계
𝑹 ∶ 집합 𝑨에서 관계 𝑹이 반사적, 대칭적, 추이적이면 ⇒ 𝑹을 동치관계라고 부른다.
나머지 함수
나머지 함수는 하나의 식을 다른 값으로 나눈 뒤 나머지를 구하는 함수이다. 예를 들어, \(8 \mod 5 = 3\)이고 \(13 \mod 5 = 3\)이다. 두 정수 \(m\), \(n\)에 대해 양의 정수 \(d\)로 나머지 연산을 하였을 때, 같은 값이 나오는 경우가 있는데 이때의 \(m\)과 \(n\)은 \(d\)에 관한 모듈로 합동이라 하고, \(m \equiv n \pmod{d}\)로 표기한다. 예를 들어, 8과 13은 5에 관한 모듈로-5 합동이라는 사실을 \(8 \equiv 13 \pmod{5}\)와 같이 표기한다.
\(m \equiv n \pmod{3}\)을 만족하는 \((m, n)\)의 순서쌍들의 집합을 관계 \(R\)이라 했을 때, 다음을 만족한다.
1. 임의의 \(a\)에 대해서 \(a \equiv a \pmod{3}\)이다.
2. \(a \equiv b \pmod{3}\)이면, \(b \equiv a \pmod{3}\)이다.
3. \(a \equiv b \pmod{3}\)이고, \(b \equiv c \pmod{3}\)이면, \(a \equiv c \pmod{3}\)이다.
위의 사실로부터 3에 관한 모듈로 합동은 반사적, 대칭적, 추이적 성질을 만족하므로 동치관계이다. 그리고 3 대신에 임의의 자연수를 대입하더라도 항상 반사적, 대칭적, 추이적임을 보일 수 있기 때문에 모듈로 합동 관계는 항상 동치관계임을 알 수 있다.
📌 예시: 다음 모듈로 합동의 참, 거짓 여부를 판별하시오.
1) \(6 \equiv 16 \pmod{10}\)
2) \(3 \equiv 6 \pmod{7}\)
1) 6 mod 10 = 6, 16 mod 10 = 6이므로 참
2) 3 mod 7 = 3, 6 mod 7 = 6이므로 거짓
(4) 동치류
\( A \) : 집합
\( R \) : \( A \)에서의 동치관계
\( A \)의 임의의 원소 \( a \)에 대해서
\[ [a] = \{ x \in A \mid (a, x) \in R \} \]
이를 \( a \)의 동치류라고 부른다.
📌 예제: 집합 \( A = \{0, 1, 2\} \)에서의 관계 \( R = \{(0, 0), (1, 1), (1, 2), (2, 1), (2, 2)\} \)에 관해 서로 다른 동치류를 모두 찾으시오.
우선, 관계 \( R \)이 동치 관계인지 확인해 보자. 동치 관계가 되기 위해서는 반사성, 대칭성, 추이성을 만족해야 한다.
1. 반사성 (Reflexive):
- 모든 \( a \in A \)에 대해 \( (a, a) \in R \)이어야 한다.
- \( R \)에 \( (0, 0), (1, 1), (2, 2) \)가 있으므로 반사성을 만족한다.
2. 대칭성 (Symmetric):
- 모든 \( (a, b) \in R \)에 대해 \( (b, a) \in R \)이어야 한다.
- \( R \)에 \( (1, 2) \)가 있으므로 \( (2, 1) \)도 있습니다. 대칭성을 만족한다.
3. 추이성 (Transitive):
- \( (a, b) \in R \)이고 \( (b, c) \in R \)이면 \( (a, c) \in R \)이어야 한다.
- \( R \)에서 확인해 보면 \( (1, 2) \)와 \( (2, 1) \)로부터 \( (1, 1) \)가 필요합니다. \( (1, 1) \)은 이미 \( R \)에 포함되어 있다. 따라서 추이성을 만족한다.
따라서 \( R \)은 동치 관계이다.
이제 이 관계에 대한 동치류를 찾아보자.
동치류는 각 원소가 속하는 집합으로 나눌 수 있다.
- 0에 대한 동치류: \([0] = \{0\}\)
- 1에 대한 동치류: \([1] = \{1, 2\}\)
- 2에 대한 동치류: \([2] = \{1, 2\}\)
따라서 서로 다른 동치류는 다음과 같다.
\[ \{0\}, \{1, 2\} \]
참고자료: 이산수학 | 손진곤 (지은이) 한국방송통신대학교출판문화원
'CS > 이산수학' 카테고리의 다른 글
| 이산수학 - 그래프, 트레일, 경로, 이분 그래프, 완전 이분 그래프, 정규 그래프, 오일러 투어, 해밀턴 경로 (0) | 2024.05.15 |
|---|---|
| 이산수학 - 함수, 함수의 상등, 전사함수, 단사함수, 합성함수, 계승함수, 바닥함수, 천장함수, 나머지 함수 (0) | 2024.05.15 |
| 이산수학 - 행렬: 행렬의 연산, 종류, 정방행렬, 단위행렬, 역대칭행렬, 삼각행렬, 역행렬, 부울행렬 (0) | 2024.05.15 |
| 이산수학 - 집합, 집합 연산, 합집합, 교집합, 차집합, 대칭차집합, 대수 법칙 (0) | 2024.05.13 |
| 이산수학 - 증명, 직접증명법, 수학적 귀납법, 간접증명법, 다양한 증명방법 (0) | 2024.05.13 |



