1. 기본사항
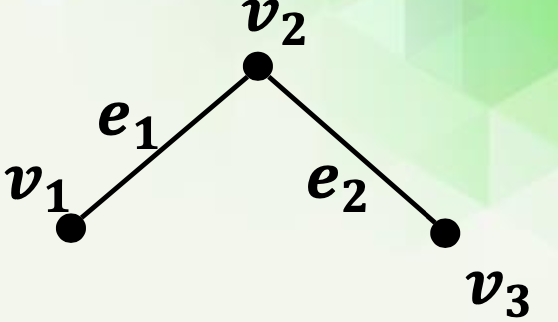
다음 그림처럼 점과 두 점을 서로 연결하는 선으로 이루어진 도형을 그래프라 한다.
2. 주요 용어
그래프 \( G \)는 꼭지점(vertex)들과 변(edge)들로 구성된다. 이를 수식으로 나타내면 \( G = (V, E) \)이다. 여기서 \( V = \{ v | v \text{는 꼭지점} \} \)이고, \( E = \{ e | e \text{는 변} \} \)이다.
변은 두 꼭지점을 연결한다. 즉, 변에 의해 발생(incident)된다고 한다.
연결된 두 꼭지점은 서로 인접(adjacent)한다고 한다.
병렬 변(parallel edge)은 두 꼭지점을 연결하는 변이 복수개 있을 때를 의미한다.
루프(loop)는 동일한 꼭지점을 연결하는 변을 뜻한다.
고립된 꼭지점(isolated vertex)은 어떠한 변도 연결되지 않은 꼭지점을 의미한다.
동형(isomorphic): 꼭지점과 변의 이름만 제외하고는 모두 동일한 그래프들을 서로 동형이라고 함.
다음은 방향 그래프와 무향 그래프에 대한 설명이다.
방향 그래프(directed graph)는 변이 방향을 가지고 있는 그래프이다. 이 그래프에서는 변의 방향이 중요하며, 각 변은 시작점과 끝점을 갖는다.
무향 그래프(undirected graph)는 변이 방향을 가지고 있지 않은 그래프이다. 이 그래프에서는 변의 방향이 없으며, 각 변은 단순히 두 정점을 연결한다.
단순 그래프는 루프(loop)와 병렬 변(parallel edge)을 가지지 않는 무향 그래프이다.
- 루프(loop): 자기 자신을 연결하는 변
- 병렬 변(parallel edge): 두 정점을 연결하는 여러 변
즉, 단순 그래프는 다음과 같은 특성을 가진다.
1. 두 정점을 연결하는 변이 하나뿐이다.
2. 루프가 없다.
이러한 그래프는 수학적으로 다음과 같이 표현할 수 있다.
단순 그래프 \( G \)는 정점 \( V \)와 변 \( E \)로 구성되며, 이는 다음과 같이 나타낼 수 있다.
\[ G = (V, E) \]
여기서, \( V \)는 그래프의 정점 집합이고, \( E \)는 그래프의 변 집합이다. 변 집합 \( E \)는 다음 조건을 만족한다:
\[ E \subseteq \{ \{u, v\} \mid u, v \in V \text{이고} u \neq v \} \]
이때, \( \{u, v\} \)는 정점 \( u \)와 정점 \( v \)를 연결하는 변을 나타낸다.

부분그래프 및 신장 부분 그래프:
\( G = (V, E) \), \( H = (V', E') \)가 그래프
(1) \( V' \subseteq V \), \( E' \subseteq E \)
⇒ \( H \)를 \( G \)의 부분 그래프(subgraph)
(2) \( V' = V \), \( E' \subseteq E \)
⇒ \( H \)를 \( G \)의 신장 부분 그래프(spanning subgraph)
그래프 \( G \)는 \( V \)와 \( E \)로 구성되며, \( \mathbf{v} \in V \)이다.
차수 (Degree)
- \( \mathbf{v} \)의 차수 \( \deg(\mathbf{v}) \): \( \mathbf{v} \)에 인접한 변의 개수를 의미한다.
- \( G \)의 총 차수 (Total Degree) \( \deg(G) \): \( G \)에 속한 모든 꼭지점의 차수의 합이다.
\[
\deg(G) = \sum_{\mathbf{v} \in V} \deg(\mathbf{v})
\]
방향 그래프에서:
1. \( \mathbf{v} \)의 진입차수 (In-Degree): \( \mathbf{v} \)로 들어오는 변의 수이다.
2. \( \mathbf{v} \)의 진출차수 (Out-Degree): \( \mathbf{v} \)에서 나가는 변의 수이다.
📌 예시: 𝑮의 총 차수?
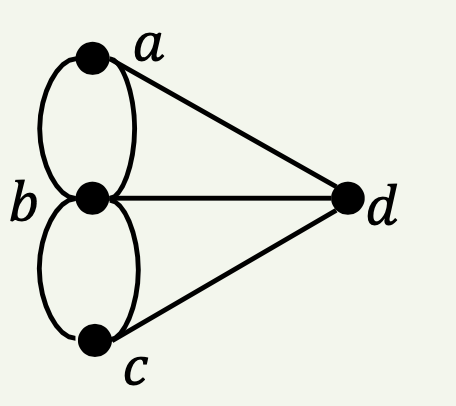
𝒅𝒆𝒈 (𝒂) = 𝟑
𝒅𝒆𝒈 (𝒃) = 𝟓
𝒅𝒆𝒈 (𝒄) = 𝟑
𝒅𝒆𝒈 (𝒅) = 𝟑
∴ 𝒅𝒆𝒈 (𝑮) = 14
정리 Handshaking Lemma
\[ G = (V, E) \]
\[ \sum_{v \in V} \deg(v) = 2|E| \]
그래프에서 차수가 홀수인 꼭지점의 수는 짝수이다.
그래프 탐색
\[ G(V, E), \quad v_0, v_k \in V \]
1. \( v_0 \)에서 \( v_k \)까지의 워크(walk)
- \( v_0 \)에서 시작하여 \( v_k \)에 도착하는 꼭지점과 변들을 순서대로 나열한 것
- \( W = v_0 e_1 v_1 e_2 v_2 \cdots e_k v_k \)
\[
\Rightarrow v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_k
\]
\[
\Rightarrow e_1 e_2 e_3 \cdots e_k
\]
- \( v_0 \): 시작점, \( v_k \): 종점, \( v_1, v_2, \cdots, v_{k-1} \): 내부점
- \( k \): \( W \)의 길이(length)
- \( v_0 = v_k \)일 때 \( W \)는 닫혀있다(closed)
2. 워크 \( W \)의 변들이 모두 서로 다르면 \( W \)를 트레일(trail)이라고 한다.
3. 트레일 \( W \)의 꼭지점이 모두 다르면 \( W \)를 경로(path)라고 한다.
참고
\[ \text{path} \subseteq \text{trail} \subseteq \text{walk} \]
\[ G = (V, E), \quad W = v_0 e_1 v_1 e_2 v_2 \cdots e_k v_k \] : 워크
1. \( W \)가 트레일이고 \( v_0 = v_k \)이면 \( W \)는 닫힌 트레일이다.
2. \( W \)가 경로이고 \( v_0 = v_k \)이면 \( W \)는 닫힌 경로로서 사이클(cycle)이다.
- 길이가 \( k \)인 사이클을 \( k \)-사이클이라 한다.
𝑮 = (𝑽, 𝑬): 그래프, 𝒖, 𝒗 ∈ 𝑽
- 𝒖에서 𝒗로 가는 경로가 존재하면 ⇒ 𝒖와 𝒗는 서로 연결되어 있다.
- 𝑽의 꼭지점들은 서로 연결되고 다른 집합과 겹치지 않는 꼭지점들의 집합 𝑽_1, 𝑽_2, ⋯, 𝑽_𝒏으로 나눌 수 있다.
⇒ 𝑽_1, 𝑽_2, ⋯, 𝑽_𝒏을 𝑮의 연결 성분이라 한다.
- ∀ 𝒖, ∀ 𝒗 ∈ 𝑽, 𝒖에서 𝒗로 가는 경로가 존재하면
⇒ 𝑮는 연결 그래프 (connected graph)이다.
⇒ 𝑮는 오직 하나의 연결 성분으로 구성된다.
2. 그래프의 종류
완전 그래프
\(G = (V, E)\)는 그래프이다.
모든 \(u, v \in V\)에 대해, \(\exists e = (u, v) \in E\)이면 \(G\)는 완전 그래프(complete graph)이다.
완전 그래프는 \(K_n\)으로 나타내며, 여기서 \(V = n\)인 완전 그래프를 의미한다.
\[
G = (V, E) : \text{그래프}
\]
\[
\forall u, \forall v \in V, \exists e = (u, v) \in E \implies G \text{는 완전 그래프(complete graph)}이다.
\]
\[
K_n : V = n \text{인 완전 그래프}
\]
완전 그래프는 임의의 두 꼭지점을 연결하는 변이 항상 존재하는 그래프

완전 그래프 𝑲𝒏는 𝒏(𝒏−𝟏)/2개의 변을 가지며 𝟐 모든 꼭지점의 차수는 𝒏 − 𝟏임.
이분 그래프
그래프 \( G = (V, E) \)가 있다. 여기서 \( V \)는 꼭지점의 집합이고 \( E \)는 변의 집합이다. 이 그래프에서 \( V \)는 연결 성분 \( V_1 \)과 \( V_2 \)로 분할되어 있다. 모든 변들이 \( V_1 \)의 꼭지점과 \( V_2 \)의 꼭지점을 인접시키는 경우, 이 그래프 \( G \)를 이분 그래프(bipartite graph)라고 한다.
1. \( V_1 \cup V_2 = V \), \( V_1 \cap V_2 = \emptyset \)
2. \( \forall e = (v_1, v_2) \in E, \, v_1 \in V_1, \, v_2 \in V_2 \)

이분 그래프의 정의를 다르게 표현하면, 그래프의 꼭지점을 두 가지 색으로 칠할 때, 모든 변의 양 꼭지점이 서로 다른 색으로 칠해질 수 있는 그래프라고 할 수 있다.
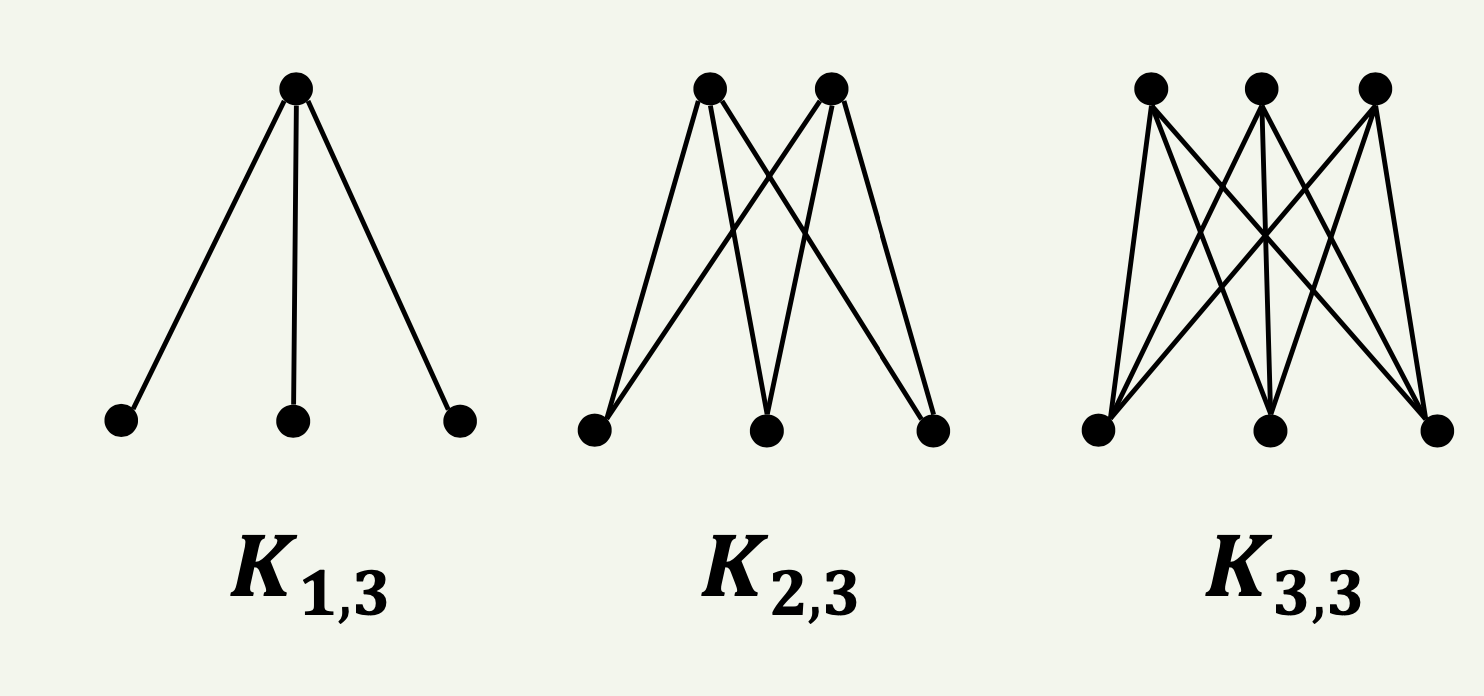
완전 이분 그래프
그래프 \( G = (V, E) \)에서 이분 그래프는 두 개의 분리된 정점 집합 \( V_1 \)과 \( V_2 \)로 이루어져 있다. 즉, \( V_1 \cap V_2 = \emptyset \)이며, \( V_1 \cup V_2 = V \)이다. 이때 모든 \( v_1 \in V_1 \)와 \( v_2 \in V_2 \)에 대해 항상 \( (v_1, v_2) \in E \)인 간선이 존재하면, 이 그래프 \( G \)를 완전 이분 그래프(complete bipartite graph)라 한다. 이를 수식으로 표현하면 다음과 같다.
\[ G = (V, E) \]
\[ V_1 \cap V_2 = \emptyset, \quad V_1 \cup V_2 = V \]
\[ \forall v_1 \in V_1, \forall v_2 \in V_2, \exists e = (v_1, v_2) \in E \]
완전 이분 그래프는 일반적으로 \( K_{m,n} \)으로 표기되며, 여기서 \( V_1 \)의 정점의 수가 \( m \), \( V_2 \)의 정점의 수가 \( n \)이다. 따라서 \( K_{m,n} \)은 \( V_1 \)에 \( m \)개의 정점, \( V_2 \)에 \( n \)개의 정점을 가진 완전 이분 그래프를 의미한다.
비교를 위해 일반적인 이분 그래프와 완전 이분 그래프의 차이를 다시 정리하면, 일반적인 이분 그래프에서는 모든 \( v_1 \in V_1 \)와 \( v_2 \in V_2 \) 사이에 간선이 존재할 필요는 없지만, 완전 이분 그래프에서는 반드시 간선이 존재해야 한다는 점이다. 이는 다음과 같은 수식으로 나타낼 수 있다.
\[ \forall e = (v_1, v_2) \in E, \quad v_1 \in V_1, \quad v_2 \in V_2 \]
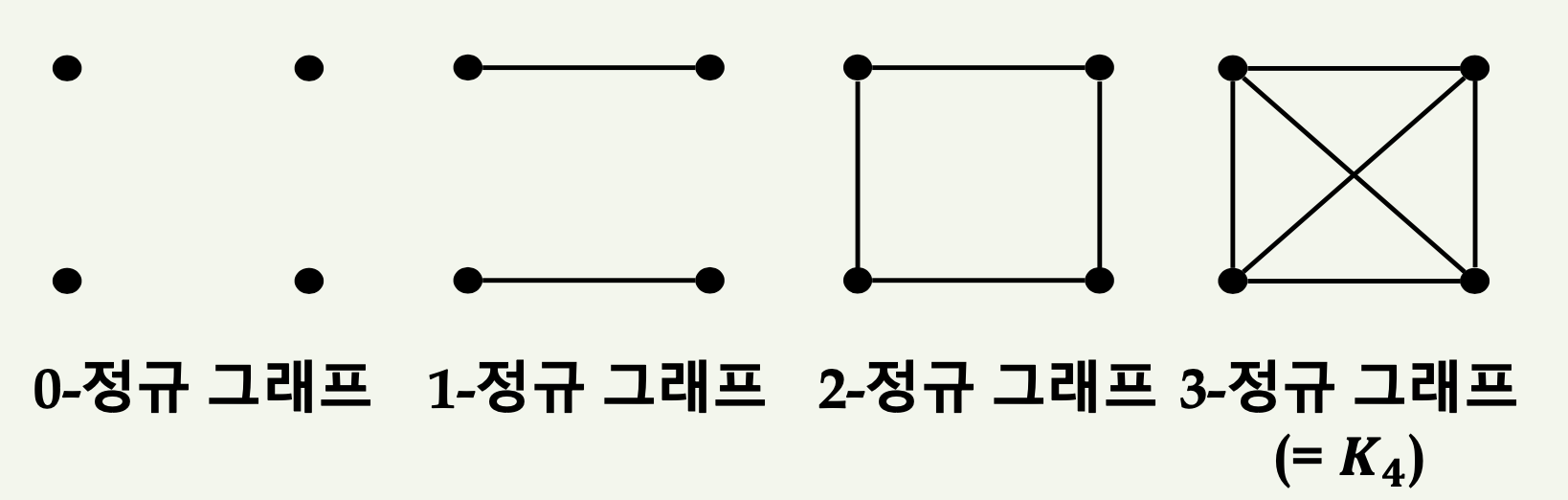
k-정규 그래프
k-정규 그래프는 그래프 \( G = (V, E) \)에서 모든 꼭지점들이 동일한 수의 인접한 꼭지점을 갖는 경우를 말한다. 이러한 그래프를 정규 그래프(regular graph)라고 부른다. 정규 그래프 \( G \)는 모든 꼭지점이 동일한 차수를 갖는다. 즉, 모든 \( v \in V \)에 대해 \( \text{deg}(v) = k \)이다. 따라서, \( G \)를 \( k \)-정규 그래프(k-regular graph)라고 한다.
이를 수식으로 표현하면 다음과 같다:
\( G = (V, E) \)
\( \forall v \in V, \text{deg}(v) = k \)
이때, \( G \)는 \( k \)-정규 그래프이다.
완전 그래프는 임의의 두 꼭지점을 연결하는 변이 항상 존재하는 그래프
∴ 완전그래프 𝑲𝒏는 (n-1)-정규 그래프
3. 그래프의 표현
(1) 발생 행렬
그래프 \( G = (V, E) \)는 꼭지점을 행으로, 변을 열로 하여 변과 꼭지점 사이의 발생관계를 표현한 행렬을 발생행렬이라 한다. 발생행렬 \( M_I = (a_{ij}) \)는 다음과 같다:
\[
M_I = (a_{ij})
\]
여기서, 발생행렬 \( M_I \)는 \(|V| \times |E|\) 크기의 부울 행렬이다.
\[
a_{ij} =
\begin{cases}
1 & \text{if } v_i \text{가 } e_j \text{에 의해 발생되는 경우} \\
0 & \text{그 밖의 경우}
\end{cases}
\]
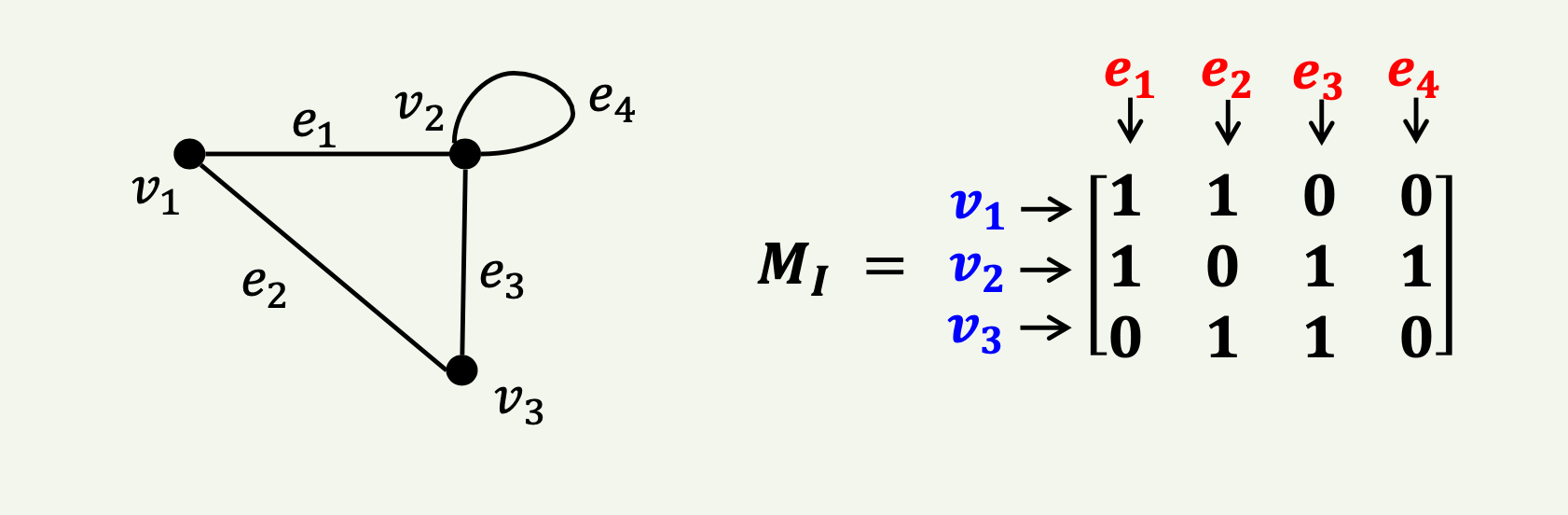
(2) 인접 행렬
그래프 \( G = (V, E) \)는 꼭지점을 행과 열로 하여 꼭지점과 꼭지점 사이의 인접관계를 표현한 행렬을 통해 나타낼 수 있다. 이러한 행렬을 인접행렬 \( M_A = (a_{ij}) \)이라 한다.
인접행렬 \( M_A \)는 다음과 같은 특성을 가진다:
- \( |V| \times |V| \) 크기의 행렬이다.
- \( a_{ij} \)는 꼭지점 \( v_i \)에서 꼭지점 \( v_j \)로의 연결 개수를 나타낸다.
(3) 인접 리스트
𝑮 = (𝑽, 𝑬)는 그래프이다.
각 꼭지점에 인접하는 꼭지점들을 차례로 연결 리스트로 표현한 것이다.

\[
\begin{array}{l}
v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow \text{null} \\
v_2 \rightarrow v_1 \rightarrow v_3 \rightarrow \text{null} \\
v_3 \rightarrow v_1 \rightarrow v_2 \rightarrow v_4 \rightarrow \text{null} \\
v_4 \rightarrow v_3 \rightarrow \text{null}
\end{array}
\]
4. 그래프의 탐색
(1) 평면 그래프와 4색 정리
평면 그래프(planar graph)는 그래프의 모든 변(edge)을 서로 교차하지 않게 그릴 수 있는 그래프를 의미한다.
그래프 \( G = (V, E) \)가 주어졌을 때, 이 그래프가 평면 그래프인지 확인하려면, 그래프를 평면에 그렸을 때 어떤 두 변도 서로 교차하지 않아야 한다. 이는 모든 변이 서로 교차하지 않도록 배치할 수 있는지를 보는 것이다.
예를 들어, 그래프 \( G \)가 다음과 같은 두 변을 가진다고 가정한다:
\[ e_1 = (v_1, v_2) \]
\[ e_2 = (v_3, v_4) \]
이 두 변 \( e_1 \)과 \( e_2 \)는 평면에 그릴 때 서로 교차하지 않아야 한다.
평면 그래프의 대표적인 예로는 \( K_4 \) 그래프가 있다. \( K_4 \) 그래프는 4개의 정점과 6개의 변을 가지며, 평면에 그렸을 때 모든 변이 서로 교차하지 않도록 그릴 수 있다. 이때, \( K_4 \) 그래프의 평면 표현은 다음과 같은 형태를 띤다:
\[ \begin{array}{c}
\bullet \\
/ | \\
\bullet - \bullet \\
\backslash | \\
\bullet
\end{array} \]
평면 그래프의 정의를 좀 더 일반화하면, 임의의 그래프 \( G \)가 주어졌을 때 이 그래프가 평면 그래프가 되기 위한 조건은 Kuratowski의 정리에 의해 다음과 같이 주어진다.
그래프 \( G \)는 \( K_5 \)나 \( K_{3,3} \)의 서브그래프를 포함하지 않을 때 평면 그래프가 된다.
즉, 평면 그래프는 어떤 방법으로든 평면에 그렸을 때 두 변이 서로 교차하지 않는 그래프를 의미한다.
📌 평면 그래프가 아닌 예
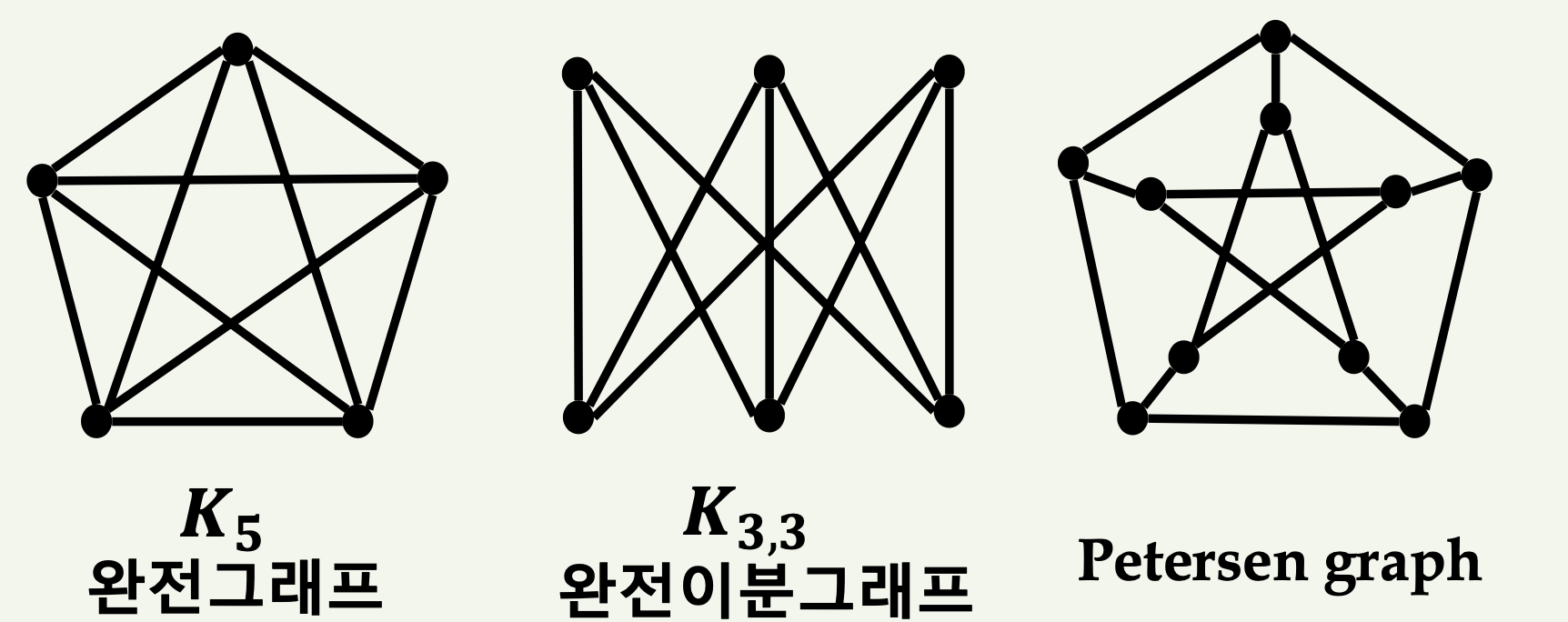
📌 평면 그래프의 예

오일러의 공식
오일러의 공식은 연결된 평면 그래프에서 면(face), 변들로 만들어지는 사이클을 경계로 형성된 공간을 정의하는 중요한 개념이다.
[정의] 연결된 평면 그래프에서 면은 변들로 만들어지는 사이클을 경계로 형성된 공간이다.
\[
f_1 : \text{사이클}(1, 2, 3, 1)을 경계
\]
\[
f_2 : \text{사이클}(2, 3, 4, 2)을 경계
\]
\[
f_3 : \text{사이클}(1, 3, 4, 5, 4, 1)을 경계
\]
\[
f_4 : \text{사이클}(1, 2, 4, 1)을 경계
\]
연결된 평면 그래프에서 꼭지점의 수를 𝒗, 변의 수를 𝒆, 면의 수를 𝒇라고 하면 𝒗 − 𝒆 + 𝒇 = 𝟐 이다.
4색 정리
평면 그래프가 주어졌을 때, 각 꼭지점에 대하여 인접한 꼭지점과 서로 다른 색으로 칠하는데 필요한 색은 4가지이면 충분하다.

(2) 오일러 투어
오일러 트레일(Eulerian trail)은 그래프의 모든 변을 각각 한 번만 지나는 트레일이다.
오일러 투어(Eulerian tour, Eulerian circuit, Eulerian cycle)는 닫힌 오일러 트레일이다. 즉, 시작점과 종점이 같은 오일러 트레일을 말한다.
수식으로 표현하면 다음과 같다. 그래프 \( G = (V, E) \)가 주어졌을 때, 오일러 트레일은 모든 변 \( e \in E \)를 한 번씩만 지나는 경로 \( P \)를 의미한다. 오일러 투어는 시작점과 종점이 동일한 경로이다.
오일러 트레일의 조건은 다음과 같다.
1. 그래프가 연결 그래프이어야 한다.
2. 홀수 차수의 정점이 0개 또는 2개여야 한다.
오일러 투어의 조건은 다음과 같다.
1. 그래프가 연결 그래프이어야 한다.
2. 모든 정점의 차수가 짝수여야 한다.
연결 그래프가 오일러 투어를 가지기 위한 필요충분 조건은 그래프의 모든 꼭지점의 차수는 짝수인 것이다.
즉,
연결 그래프 𝑮의 모든 꼭지점의 차수는 짝수이면 𝑮는 오일러 그래프이다.
(3) 해밀턴 경로
해밀턴 경로 (Hamiltonian path)는 그래프의 모든 꼭지점들을 한 번씩만 지나는 경로이다.
해밀턴 사이클 (Hamiltonian cycle)은 닫힌 해밀턴 경로로, 시작점과 종점이 같은 해밀턴 경로이다.
수식으로 표현하면 다음과 같다:
해밀턴 경로:
$$ P = \{v_1, v_2, \ldots, v_n\} $$
여기서 \( v_i \)는 꼭지점을 의미하며, 모든 꼭지점 \( v_i \)는 한 번씩만 나타난다.
해밀턴 사이클:
$$ C = \{v_1, v_2, \ldots, v_n, v_1\} $$
여기서 \( v_1 \)은 시작점이자 종점이 된다. 따라서 사이클은 꼭지점 \( v_1 \)에서 시작하여 모든 꼭지점을 한 번씩만 지나고 다시 \( v_1 \)으로 돌아온다.

5. 그래프의 활용
(1) 가중 그래프
▪ 가중 그래프 (weighted graph)
가중 그래프는 그래프의 각 변에 실수값이 붙여진 그래프이다. 변에 부여된 값은 가중치(weight)라고 한다.
수식으로 표현하면, 가중 그래프 \(G\)는 다음과 같다:
\[ G = (V, E, w) \]
여기서
- \(V\)는 정점들의 집합이다.
- \(E\)는 변들의 집합이다.
- \(w: E \rightarrow \mathbb{R}\)는 변 \(e \in E\)에 가중치 \(w(e)\)를 부여하는 함수이다.
예를 들어, 정점 \(V = \{v_1, v_2, v_3\}\)와 변 \(E = \{e_1, e_2, e_3\}\)가 있는 경우, 가중치는 다음과 같이 나타낼 수 있다:
\[ w(e_1) = 2.5, \quad w(e_2) = 1.2, \quad w(e_3) = 3.8 \]
(2) 최단 경로 문제
출발지와 도착지가 주어졌을 때 가장 짧은 경로를 찾는 문제이다.
참고자료: 이산수학 | 손진곤 (지은이) 한국방송통신대학교출판문화원
'CS > 이산수학' 카테고리의 다른 글
| 이산수학 - 조합론 (1) | 2024.05.16 |
|---|---|
| 이산수학 - 정수론, 나눗셈, 베주의 항등식, 유클리드 호제법, 나머지 연산, 소수와 소인수 분해, RSA 암호 (0) | 2024.05.15 |
| 이산수학 - 함수, 함수의 상등, 전사함수, 단사함수, 합성함수, 계승함수, 바닥함수, 천장함수, 나머지 함수 (0) | 2024.05.15 |
| 이산수학 - 관계, 관계의 표현, 관계의 성질, 관계의 종류, 반사적, 대칭적, 추이적, 동치관계 (0) | 2024.05.15 |
| 이산수학 - 행렬: 행렬의 연산, 종류, 정방행렬, 단위행렬, 역대칭행렬, 삼각행렬, 역행렬, 부울행렬 (0) | 2024.05.15 |



