이산수학 - 행렬: 행렬의 연산, 종류, 정방행렬, 단위행렬, 역대칭행렬, 삼각행렬, 역행렬, 부울행렬

 

1. 기본 사항 

행렬은 행과 열로 구성되는 사각형 형태로 수를 배열한 것 

 

$$\left[\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\\ 9& 0& 2& 5\end{array}\right]$$

 

 

- 컴퓨터 분야의 활용

• 프로그래밍 언어
• 자료구조
• 컴퓨터 그래픽스
• 패턴인식
• 로봇동작
• 인공지능

행렬 

 

m과 n이 양의 정수일 때, m개의 행과 n개의 열로 구성된 직사각형의 수 배열 A를 $m\times n$ 행렬이라 한다.

행렬 $A$에서 i번째 행의 j번째 열의 수를 행렬 $A$의 $(i,j)$ 원소라 하며, $a_{ij}$로 표시한다. 행렬 $A$를 간단히 $A=[a_{ij}]$로 표기하기도 한다.

- 행 벡터(row vector): $1\times n$ 행렬
- 열 벡터(column vector): $m\times 1$ 행렬

 

영행렬 

 

모든 원소가 0인 행렬을 영행렬이라고 한다. 행렬의 크기에 따라 다음과 같이 다양한 영행렬이 존재한다. 

$$\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0\end{array}\right]$$

여기서 각 행과 열의 원소는 모두 0이다. 영행렬은 크기에 따라 다양하게 표현될 수 있다. 

 

 

 

2. 행렬의 연산 

 

(1) 기본 연산 

 

행렬에도 실수 집합에서의 사칙 연산과 유사한 다양한 연산이 존재한다. 행렬의 곱셉은 스칼라 곱과 행렬곱이 있는데, 스칼라 곱은 실수의 곱셈과 유사한 성질을 가지고 있어 쉽게 이해할 수 있다. 

 

행렬의 합, 차, 스칼라 곱 

 

- 행렬의 합: 𝑨 + 𝑩 는 같은 위치의 𝑨와 𝑩의 원소를 더해서 구해지는 행렬로서 (𝒊, 𝒋) 원소의 값은 𝒂𝒊𝒋 + 𝒃𝒊𝒋 이다.

- 행렬의 차: 𝑨 − 𝑩 는 같은 위치의 𝑨의 원소로부터 𝑩의 원소를 빼서 구해지는 행렬로서 (𝒊, 𝒋) 원소의 값은 𝒂𝒊𝒋 − 𝒃𝒊𝒋 이다.

- 스칼라 곱: 𝒌𝑨는 𝑨 의 각 원소에 𝒌 를 곱해서 구해지는 행렬로서 (𝒊, 𝒋) 원소의 값은 𝒌𝒂𝒊𝒋 이다.

 

 

다음과 같은 예시를 풀어보자. 

 

예시: 행렬 A와 B가 다음과 같을 때 

 

A = $$\left[\begin{array}{cccc}1& 1& 0& 0\\ 0& 1& 1& 0\\ 0& 0& 1& 1\end{array}\right]$$

B = $$\left[\begin{array}{cccc}2& 4& 1& 3\\ 1& 4& 2& 3\\ 2& 3& 1& 6\end{array}\right]$$

 

1)

B - A = $$\left[\begin{array}{cccc}1& 3& 1& 3\\ 1& 3& 1& 3\\ 2& 3& 0& 5\end{array}\right]$$

 

2) 

2A = $$\left[\begin{array}{cccc}2& 2& 0& 0\\ 0& 2& 2& 0\\ 0& 0& 2& 2\end{array}\right]$$

 

 

3) 

2A + (B - A) = $$\left[\begin{array}{cccc}3& 5& 1& 3\\ 1& 5& 3& 3\\ 2& 3& 2& 7\end{array}\right]$$
  

 

 

행렬의 합과 스칼라 곱의 연산법칙 

행렬의 합과 스칼라 곱은 같은 크기의 행렬𝑨,𝑩,𝑪에 대해 다음과 같은 연산법칙들을 만족한다.
(𝒂, 𝒃는 실수이고 𝑶은 모든 원소가 0인 영행렬을 의미한다.)\

 

(1) 합의 교환법칙: 𝑨+𝑩=𝑩+𝑨 

(2) 합의 결합법칙: 𝑨+ 𝑩+𝑪 = 𝑨+𝑩 +𝑪

(3) 합의 항등원: 𝑨+𝑶=𝑨
(4) 합의 역원:  𝑨+(−𝑨)=𝑶

(5) 스칼라 곱의 결합법칙: (𝒂𝒃)𝑨 = 𝒂(𝒃𝑨)

(6) 스칼라 곱의 분배법칙: (𝒂+𝒃)𝑨=𝒂𝑨+𝒃𝑨

(7) 스칼라 곱의 결합법칙: (𝒂−𝒃)𝑨=𝒂𝑨−𝒃𝑨

(8)스칼라 곱의 결합법칙:  𝒂(𝑨+𝑩) =𝒂𝑨+𝒂𝑩

(9)스칼라 곱의 결합법칙:  𝒂(𝑨−𝑩) =𝒂𝑨−𝒂𝑩

 

 

행렬의 곱 

𝑨가 𝒎×𝒏 행렬이고 𝑩가 𝒏×𝒍 행렬일 때,  행렬의 곱 𝑨𝑩는 (𝒊, 𝒋)원소가 다음과 같이  정의되는 𝒎 × 𝒍 행렬이다.

 

$$A{B}_{ij}=\sum _{k=1}^n{a}_{ik}{b}_{kj}=a_{i1}{b}_{1j}+a_{i2}{b}_{2j}+\cdots +a_{in}{b}_{nj}$$

 

 

 

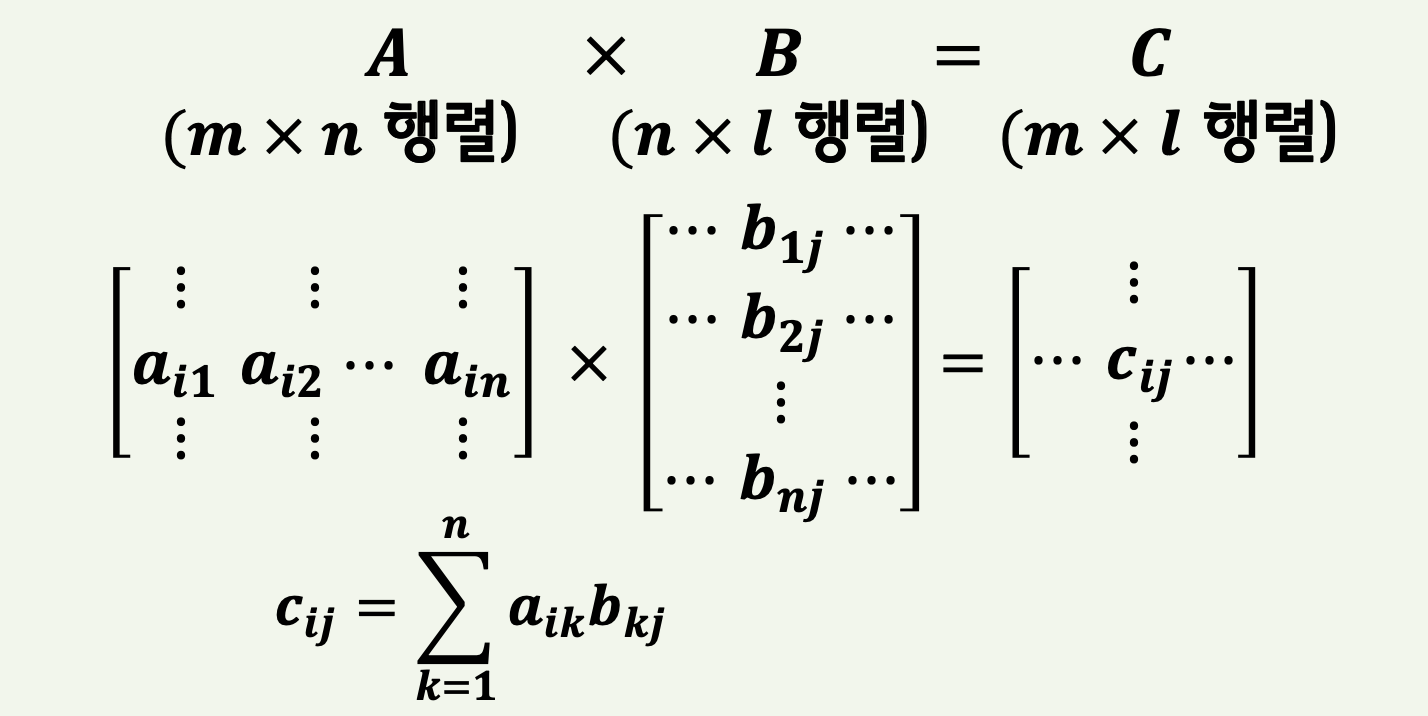
벡터의 내적 

$$A=(a_1,a_2,\dots ,a_n)\text{와 }B=(b_1,b_2,\dots ,b_n)\text{가 }n\text{ 차원 벡터라고 할 때,}$$
$$A\text{와 }B\text{의 내적(inner product) }A\cdot B\text{는 다음과 같이 정의한다.}$$
$$A\cdot B=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n$$

 

$$\begin{gathered} \text{예를 들어,} \\ A=(1,2,3),B=(-1,0,2)\text{이면} \\ A\cdot B=1\cdot (-1)+2\cdot 0+3\cdot 2=-1+0+6=5 \end{gathered}$$

 

 

 

예시: 행렬 A, B가 다음과 같을 때 AB를 계산하시오 

 

A = $$\left[\begin{array}{cc}4& -1\\ 2& 3\\ 1& 5\end{array}\right]$$

B =  $$\left[\begin{array}{cc}7& -3\\ 9& 2\end{array}\right]$$

 

 

풀이 : 

$$A=A\cdot B=\left[\begin{array}{cc}4& -1\\ 2& 3\\ 1& 5\end{array}\right]\left[\begin{array}{cc}7& -3\\ 9& 2\end{array}\right]=\left[\begin{array}{cc}4\times 7+(-1)\times 9& 4\times (-3)+(-1)\times 2\\ 2\times 7+3\times 9& 2\times (-3)+3\times 2\\ 1\times 7+5\times 9& 1\times (-3)+5\times 2\end{array}\right]=\left[\begin{array}{cc}28-9& -12-2\\ 14+27& -6+6\\ 7+45& -3+10\end{array}\right]=\left[\begin{array}{cc}19& -14\\ 41& 0\\ 52& 7\end{array}\right]$$

 

 

행렬 곱의 연산법칙 

 

행렬 𝑨,𝑩,𝑪가 각 연산에 적합한 크기의 행렬이라 할 때, 다음과 같은 연산법칙들을 만족한다.

 

(1) 곱의 결합법칙 : 𝑨(𝑩𝑪) = (𝑨𝑩)𝑪

(2) 곱의 분배법칙: 𝑨(𝑩+𝑪) = 𝑨𝑩+𝑨𝑪

(3) 곱의 분배법칙: (𝑨+𝑩 )𝑪 = 𝑨𝑪+𝑩𝑪

 

행렬 곱 연산에는 특이성질이 있는데  

1) 𝑨𝑩 ≠ 𝑩𝑨

2) ∃𝑨 ≠ 𝑶, ∃𝑩 ≠ 𝑶 ⇒ 𝑨𝑩 = 𝑶

 

주어진 행렬:
$$A=\left[\begin{array}{ccc}-1& 2& 6\end{array}\right],B=\left[\begin{array}{c}1\\ 4\\ 2\end{array}\right]$$

$AB$를 계산하면:
$$AB=\left[\begin{array}{ccc}-1& 2& 6\end{array}\right]\left[\begin{array}{c}1\\ 4\\ 2\end{array}\right]=\left[\begin{array}{c}19\end{array}\right]$$

$BA$를 계산하면:
$$B=\left[\begin{array}{c}1\\ 4\\ 2\end{array}\right],A=\left[\begin{array}{ccc}-1& 2& 6\end{array}\right]$$

따라서,
$$BA=\left[\begin{array}{ccc}1& 4& 2\end{array}\right]\left[\begin{array}{c}-1\\ 2\\ 6\end{array}\right]=\left[\begin{array}{ccc}-1& 2& 6\\ -4& 8& 24\\ -2& 4& 12\end{array}\right]$$

 

따라서 𝑨𝑩 ≠ 𝑩𝑨 임을 볼 수 있다. 

 

또한  두 행렬 $A$와 $B$가 영행렬이 아님에도 불구하고 그 곱이 영행렬이 될 수 있다. 

 

$$A=\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right],B=\left[\begin{array}{cc}1& 1\\ 0& 0\end{array}\right]$$

$AB$를 계산하면:
$$AB=\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 1\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$$

A 와 B가 영행렬이 아님에도 곱은 영행렬로 나타날 수 있다. 

 

 

(2) 가우스 소거법

행렬은 일차연립방정식의 풀이에 사용된다. 행렬을 이용한 가우스 소거법을 소개한다.

 

일차연릭방정식 L -> 확대행렬 A -> 행제형 행렬 A' -> 소거 행제형 행렬 -> A''

예를 들어 다음과 같은 일차 연립방정식이 있다고 가정하자.

$$-2x-5y+2z=-3$$
$$y+3z=6$$
$$x+3y=4$$

위 연립방정식을 행렬과 벡터를 이용해 나타내면 다음과 같다.

$$\left[\begin{array}{ccc}-2& -5& 2\\ 1& 3& 0\\ 0& 1& 3\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}-3\\ 6\\ 4\end{array}\right]$$

위에서 왼쪽의 $3\times 3$ 크기의 행렬을 계수행렬이라고 부르고, $(x,y,z)$를 해(solution), $(-3,6,4)$을 상수행렬(constant matrix)이라고 한다. 계수행렬과 상수 행렬 $(-3,6,4)$을 다음과 같이 묶어서 하나의 행렬로 만들 수 있다.

$$\left[\begin{array}{cccc}-2& -5& 2& -3\\ 1& 3& 0& 4\\ 0& 1& 3& 6\end{array}\right]$$

이 행렬을 확대행렬이라고 한다. 확대행렬은 계수와 상수가 주어졌을 때 해를 구하는 용도로 사용된다.

일차연립방정식에서 해를 구하기 위해 식을 변형하는 작업을 세 가지로 나눌 수 있는데 이것을 기본행연산이라고 한다.

 

기본행연산(elementary row operation) 

1. 어떤 두 개의 행 위치를 서로 바꾼다(행 교환 연산).
2. 어떤 하나의 행에 0이 아닌 상수를 곱한다( 행 스케일링 연산).
3. 하나의 행에 상수를 곱한 뒤 다른 행에 더한 식으로 대체한다(행 대체 연산). 

 

일차연립방정식에서 해를 구하기 위해 식을 변형하는 첫 번째 작업은 두 식의 위치를 서로 교환하는 것이다. 예를 들어 (1)과 (2)의 위치를 교환하면 다음과 같다. 

$$\begin{array}{rl}(2)x+3y& =4\\ (1)-2x-5y+2z& =-3\\ (3)y+3z& =6\end{array}$$

 

 

이처럼 두 행의 위치를 바꾸는 작업을 행렬에서는 행교환 연산이라 한다. 연립방정식에서 식의 순서를 바꾸더라도 해는 변하지 않으므로 행 교환 연산을 수행하더라도 연립방정식의 해는 동일하게 유지된다. 

행 교환 연산을 통해 변경된 행렬은 다음과 같이 표현할 수 있다. 두 행렬 사이에 $\sim$가 의미하는 것은 서로 다른 두 개의 연립방정식이 동일한 해를 가진다는 의미이다.

$$\left(\begin{array}{cccc}1& 3& 0& 4\\ -2& -5& 2& -3\\ 0& 1& 3& 6\end{array}\right)\sim \left(\begin{array}{cccc}-2& -5& 2& -3\\ 1& 3& 0& 4\\ 0& 1& 3& 6\end{array}\right)$$

일차연립방정식에서 해를 구하기 위해 식을 변형하는 두 번째 작업은 하나의 식에 0이 아닌 상수를 곱하는 것이다. 예를 들어 식 2에 상수 2를 곱하면 새로운 식 (4)를 구할 수 있다.

$$\begin{array}{rl}2x+6y& =8\text{(4)}\\ -2x-5y+2z& =-3\text{(1)}\\ y+3z& =6\text{(3)}\end{array}$$

이처럼 하나의 행에 0이 아닌 스칼라 곱을 하는 작업을 행렬에서는 행 스케일링 연산이라 한다.

$$\left(\begin{array}{cccc}1& 3& 0& 4\\ -2& -5& 2& -3\\ 0& 1& 3& 6\end{array}\right)\sim \left(\begin{array}{cccc}2& 6& 0& 8\\ -2& -5& 2& -3\\ 0& 1& 3& 6\end{array}\right)$$

일차연립방정식에서 해를 구하기 위해 식을 변형하는 세 번째 작업은 두 개의 식을 더해 새로운 식을 만드는 것이다. 식 (4)에 상수 1을 곱하여 식 (1)에 더하면 미지수 $x$가 없어진 새로운 식 (5)를 만들 수 있다.

$$\begin{array}{rl}2x+6y& =8\text{(4)}\\ y+2z& =5\text{(5)}\\ y+3z& =6\text{(3)}\end{array}$$

새로운 식을 만들기 위해 단순합이 아니라 하나의 행에 상수를 곱한 뒤에 다른 행에 더해도 된다. 식 (4)에 -1을 곱한 뒤에 식 (3)을 더하면 미지수 $y$가 없어진 새로운 식 (6)을 만들 수 있다.

$$\begin{array}{rl}2x+6y& =8\text{(4)}\\ y+2z& =5\text{(5)}\\ z& =1\text{(6)}\end{array}$$

이처럼 하나의 행에 스칼라 곱을 수행한 결과를 다른 행에 더하는 작업을 행렬에서는 행 대체 연산이라 한다.

$$\left(\begin{array}{cccc}2& 6& 0& 8\\ -2& -5& 2& -3\\ 0& 1& 3& 6\end{array}\right)\sim \left(\begin{array}{cccc}2& 6& 0& 8\\ 0& 1& 2& 5\\ 0& 0& 1& 1\end{array}\right)$$

기존의 행렬을 변형해 새로운 확대행렬을 만든 뒤, 해를 구하기 위해서 앞에서 배운 행렬의 기본행연산을 이용하여 확대행렬을 먼저 행제형 행렬로 만들고, 그 다음 소거 행제형 행렬로 변환해야 한다. 이 과정을 가우스 소거법이라 한다.

 

 

행제형 행렬(row echelon matrix) 

다음 세 가지 조건을 만족하는 행렬을 행제형 행렬(행사다리꼴 행렬)이라고 한다. 

1. 영행이 아닌 행은 영행의 위에 있다. 
2. 행렬의 각 행에서 0이 아닌 가장 처음 나타나는 원소를 선도원소 라고 하는데, 모든 선도원소는 1이다.
3. 주어진 행의 선도원소는 그 아래 행의 선도원소보다 왼쪽에 있다. 

 

1) 
$$\left(\begin{array}{ccc}4& 0& 0\\ 2& 0& 0\\ 0& 2& 3\end{array}\right)$$

첫 번째 행 $\left(\begin{array}{ccc}4& 0& 0\end{array}\right)$의 선도원소는 4로서 1이 아니다. 따라서 행제형 행렬이 아니다.

2) 
$$\left(\begin{array}{cccc}1& 2& 0& 5\\ 0& 1& 3& 0\\ 0& 0& 0& 1\end{array}\right)$$

모든 선도원소가 1이고 연속된 두 행에서 위에 있는 행의 선도원소가 아래 행의 선도원소보다 왼쪽에 있으므로 행제형 행렬이다.

3) 
$$\left(\begin{array}{cccc}1& 4& 0& 2\\ 0& 0& 1& 3\\ 0& 1& 2& 6\end{array}\right)$$

두 번째 행의 선도원소는 세 번째 열에 있는데, 세 번째 행의 선도원소는 두 번째 열에 있어서 행제형 행렬이 아니다.

4) 
$$\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right)$$

영행이 아닌 두 번째 행이 영행인 첫 번째 행보다 아래에 있으므로 행제형 행렬이 아니다.

 

 

 

 

소거행제형 행렬 

위 조건을 만족한 행제형 행렬에 다음의 네 번째 조건도 만족시키면 소거행제형 행렬이라고 한다. 

4. 선도원소가 포함된 열에서 선도원소를 제외한 모든 원소는 0이다. 

 

1)

$$\left(\begin{array}{ccc}3& 2& 0\\ 1& 0& 4\\ 0& 1& 3\end{array}\right)$$

행제형 행렬이 아니므로 소거행제형 행렬이 아니다.

2)

$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 2& 4\\ 0& 0& 0& 1\end{array}\right)$$

세 번째 행의 선도원소가 위치한 네 번째 열의 다른 모든 원소는 0이어야 하는데, (2,4) 원소가 0이 아닌 4이다. 따라서 소거행제형 행렬이 아니다.

3)

$$\left(\begin{array}{cccc}1& 2& 6& 3\\ 0& 0& 1& 8\\ 0& 0& 0& 0\end{array}\right)$$

두 번째 행의 선도원소가 위치한 세 번째 열에서 (1,3) 원소가 6으로서 0이 아니므로 소거행제형 행렬이 아니다.

4)

$$\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right)$$

모든 조건을 만족하므로 소거행제형 행렬이다.

 

 

 

 

 

3. 행렬의 종류 

정방행렬 

$n\times n$ 행렬을 $n$차 정방행렬이라고 하며, $n$을 정방행렬의 차수라고 한다.

- $n$차 정방행렬은 다음과 같은 형태를 가진다.
  $$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

- 정방행렬의 $a_{11}$, $a_{22}$, $\dots$, $a_{nn}$ 원소를 대각원소라고 한다.
- 대각원소를 포함하는 대각선을 주대각선이라고 한다.

 

 

대각행렬 

n차 정방행렬에서 대각원소 이외의 모든 원소가 0인 행렬을 대각행렬이라 한다. 즉, $i\ne j$이면 $a_{ij}=0$이다. 대각행렬은 다음과 같은 형태로 나타낼 수 있다.

$$\left(\begin{array}{cccc}{a}_{11}& 0& \cdots & 0\\ 0& a_{22}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_{nn}\end{array}\right)$$

위와 같이 대각행렬은 대각선 원소들 $a_{11},a_{22},\dots ,a_{nn}$만이 0이 아닌 값을 가지며, 나머지 모든 원소는 0인 형태를 가진다.

 

 

 

 

 

 

단위행렬

$n$차 정방행렬에서 대각원소가 모두 1이고 나머지 원소는 모두 0인 행렬을 단위행렬이라 한다. (이를 $I_n$으로 표기.)

 

즉, $i=j$이면 $a_{ij}=1$이고, $i\ne j$이면 $a_{ij}=0$이다.

예를 들어,

$$I_2=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$$

$$I_3=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

$$I_4=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

일반적으로,

$$I_n=\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right)$$

 

 

 

대칭행렬

𝑛차 정방행렬에서 $a_{ij}=a_{ji}$인 행렬을 대칭행렬이라 한다.

$$\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{12}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{1n}& a_{2n}& \cdots & a_{nn}\end{array}\right)$$

대칭행렬은 행렬의 주대각선을 기준으로 대칭인 원소들로 이루어진다. 

 

 

 

역대칭행렬

$n$차 정방행렬에서 $a_{ij}=-a_{ji}$이고 대각원소가 모두 0인 행렬을 역대칭행렬(교대행렬)이라 한다. 즉, $i=j$이면 $a_{ij}=0$이고, $i\ne j$이면 $a_{ij}=-a_{ji}$이다.

예를 들어, 다음과 같은 형태의 행렬이 역대칭행렬이다:

$$\left(\begin{array}{cccc}0& a_{12}& \cdots & a_{1n}\\ -a_{12}& 0& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ -a_{1n}& -a_{2n}& \cdots & 0\end{array}\right)$$

 

 

📌  예시: 3차 정방행렬에서 $a_{12}=3$, $a_{13}=2$, $a_{23}=-1$의 원소를 가지는 역대칭행렬이 존재할 때 행렬의 나머지 원소를 구하시오.

역대칭행렬(antisymmetric matrix)은 행렬의 전치행렬이 그 행렬의 음수와 같다는 특성을 갖고 있다. 즉, $A^T=-A$를 만족한다. 따라서 주어진 원소들을 토대로 나머지 원소를 구하면 다음과 같은 행렬을 얻을 수 있다.

$$A=\left(\begin{array}{ccc}0& 3& 2\\ -3& 0& -1\\ -2& 1& 0\end{array}\right)$$

 

 

 

 

 

삼각행렬

 

$n$차 정방행렬에서

1. 상삼각행렬 (Upper Triangular Matrix): 주대각선 아래에 있는 모든 원소들이 0일 경우.
   - 조건: $i>j$일 때, $a_{ij}=0$
   - 예시:
     $$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ 0& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_{nn}\end{array}\right)$$

2. 하삼각행렬 (Lower Triangular Matrix): 주대각선 위에 있는 모든 원소들이 0일 경우.
   - 조건: $i<j$일 때, $a_{ij}=0$
   - 예시:
     $$B=\left(\begin{array}{cccc}{a}_{11}& 0& \cdots & 0\\ a_{21}& a_{22}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right)$$

3. 삼각행렬 (Triangular Matrix): 상삼각행렬 또는 하삼각행렬을 의미.

 

 

 

 

전치행렬

 

 

행렬 $A$가 주어졌을 때, $A$의 행과 열을 서로 교환한 행렬을 $A$의 전치행렬이라고 한다. 이를 $A^T$로 표기하며, $A^T$의 크기는 원래 행렬 $A$의 행과 열의 크기가 바뀐 형태가 된다.

즉, $m\times n$ 행렬 $A$의 전치행렬 $A^T$는 $n\times m$ 크기를 갖는다.

행렬 $A$와 그 전치행렬 $A^T$는 다음과 같이 나타낼 수 있다.

$$A=\left(\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& \cdots & a_{1n}\\ a_{21}& a_{22}& a_{23}& \cdots & a_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& a_{m3}& \cdots & a_{mn}\end{array}\right)$$

전치행렬 $A^T$는 다음과 같다.

$$A^T=\left(\begin{array}{cccc}{a}_{11}& a_{21}& \cdots & a_{m1}\\ a_{12}& a_{22}& \cdots & a_{m2}\\ a_{13}& a_{23}& \cdots & a_{m3}\\ ⋮& ⋮& \ddots & ⋮\\ a_{1n}& a_{2n}& \cdots & a_{mn}\end{array}\right)$$

이와 같이, 행렬의 전치는 행과 열을 교환하는 연산으로, 원래 행렬과 전치행렬의 행과 열의 크기가 서로 바뀌게 된다.

 

 

📌 예시: 다음 행렬들의 전치행렬을 구하시오.

 

$$A=\left(\begin{array}{cccc}1& 0& 0& 0\\ 3& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right)$$

$$B=\left(\begin{array}{ccccc}1& 0& 0& 0& 3\\ 0& 0& 1& 0& 0\end{array}\right)$$

행렬 $A$의 전치행렬은 $A^T$로 나타내며, 이는 행렬 $A$의 행과 열을 바꾼 형태이다.

$$A^T=\left(\begin{array}{ccc}1& 3& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right)$$

행렬 $B$의 전치행렬은 $B^T$로 나타내며, 이는 행렬 $B$의 행과 열을 바꾼 형태이다.

$$B^T=\left(\begin{array}{cc}1& 0\\ 0& 0\\ 0& 1\\ 0& 0\\ 3& 0\end{array}\right)$$

 

 

역행렬 

$n$ 차 정방행렬 $A$, $B$가 주어졌을 때, 

$$AB=BA=I_n$$

인 행렬 $B$가 존재하는 경우 행렬 $A$를 역가능(invertible)하다고 한다. 이때, 행렬 $B$를 행렬 $A$의 역행렬이라고 하고 $A^{-1}$로 표기한다.

 

 

 

 

 

4. 부울행렬

 

행렬의 모든 원소가 부울값(0 or 1)으로만 구성된 행렬을 부울행렬이라 한다.

 

 

부울행렬의 합, 교차, 부울곱 

크기가 $m\times n$인 두 행렬 $A=[a_{ij}]$와 $B=[b_{ij}]$가 부울행렬일 때,

1. $A$와 $B$의 합(join)은
   $(i,j)$ 원소가 $a_{ij}\vee b_{ij}$이고 크기가 $m\times n$인 부울행렬 $C$이며,
   $C=A\vee B$로 나타낸다.

2. $A$와 $B$의 교차(meet)는
   $(i,j)$ 원소가 $a_{ij}\wedge b_{ij}$이고 크기가 $m\times n$인 부울행렬 $C$이며,
   $C=A\wedge B$로 나타낸다.

3. $A$와 $B$의 부울곱(boolean product)은
   $(i,j)$ 원소가 다음과 같이 정의되는 $m\times l$ 크기의 부울행렬 $C$이며,
   $C=A\circ B$로 나타낸다.
   $$c_{ij}=(a_{i1}\wedge b_{1j})\vee (a_{i2}\wedge b_{2j})\vee \cdots \vee (a_{in}\wedge b_{nj})$$

 

 

 

📌 예시: 다음 연산을 수행하고 결과를 구하시오. 

1) OR (∨) 연산

OR 연산은 각 대응 원소가 하나라도 1이면 결과가 1이 되는 연산이다.

$$\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 1\end{array}\right)\vee \left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 0& 0\end{array}\right)$$

연산 결과는 다음과 같다.

$$\left(\begin{array}{ccc}0\vee 1& 0\vee 0& 0\vee 0\\ 0\vee 1& 0\vee 1& 0\vee 0\\ 1\vee 1& 1\vee 0& 1\vee 0\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\end{array}\right)$$

2) AND (∧) 연산

AND 연산은 각 대응 원소가 모두 1이면 결과가 1이 되는 연산이다.

$$\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 1\end{array}\right)\wedge \left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 0& 0\end{array}\right)$$

연산 결과는 다음과 같다.

$$\left(\begin{array}{ccc}0\wedge 1& 0\wedge 0& 0\wedge 0\\ 0\wedge 1& 0\wedge 1& 0\wedge 0\\ 1\wedge 1& 1\wedge 0& 1\wedge 0\end{array}\right)=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\end{array}\right)$$

3) 부울곱 연산 (⨀) 연산


$$\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 1\end{array}\right)\oplus \left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 0& 0\end{array}\right)$$

연산 결과는 다음과 같다. 

$$C_{11}=(0\wedge 1)\vee (0\wedge 1)\vee (0\wedge 1)=0$$
$$C_{12}=(0\wedge 0)\vee (0\wedge 1)\vee (0\wedge 0)=0$$
$$C_{13}=(0\wedge 0)\vee (0\wedge 0)\vee (0\wedge 0)=0$$
$$C_{21}=(0\wedge 1)\vee (0\wedge 1)\vee (0\wedge 1)=0$$
$$C_{22}=(0\wedge 0)\vee (0\wedge 1)\vee (0\wedge 0)=0$$
$$C_{23}=(0\wedge 0)\vee (0\wedge 0)\vee (0\wedge 0)=0$$
$$C_{31}=(1\wedge 1)\vee (1\wedge 1)\vee (1\wedge 1)=1$$
$$C_{32}=(1\wedge 0)\vee (1\wedge 1)\vee (1\wedge 0)=1$$
$$C_{33}=(1\wedge 0)\vee (1\wedge 0)\vee (1\wedge 0)=0$$

따라서, 부울곱 연산의 결과는

$$C=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 0\end{array}\right)$$

 

 

---

 

참고자료: 이산수학 | 손진곤 (지은이) 한국방송통신대학교출판문화원