1. 기본사항
집합론에서 집합과 원소는 무정의용어이다. 무정의용어란 정의 없이 사용하는 용어를 가리키며, 직관적으로 이해할 수 있고 지금까지 알려진 다른 용어로 정의하기 힘든 대상을 표현하기 위해 사용된다.
S가 집합이라고 할 때, a를 S의 원소이고, b가 S의 원소가 아니라면 다음과 같이 표기한다.
a ∈ S, b ∉ S
다음의 항목들이 집합인지 아닌지 판별해보자.
1) { a, b, c}
2) a
3) {{a}, b}
4) { a, b, a, c}
2)는 집합 표시가 없으므로 집합이 아니다. 4는 원소 a가 중복되므로 집합이 아니다.
집합을 서술하기 위해서는 원소나열법과 조건제시법을 사용한다.
1) 원소나열법: S = {1, 2, 3}
2) 조건나열법: S = {x | 0 ≤ x < 4 인 자연수}
집합의 크기는 | S | 로 표기한다.
(1) 부분 집합
집합들 사이에 포함관계가 있을 때 부분집합으로 나타낸다. 즉, 어떤 집합 A의 모든 원소가 집합 B에 포함될 경우 A는 B의 부분집합이라고 한다. 이를 기호로
A ⊆ B 또는 A ⊂ B로 표기한다.
즉, A ⊆ B ↔ ∀x (x ∈ A → x ∈ B)
진부분집합(proper subset)은 A가 B의 부분집합이고 A≠B 라면 A는 B의 진부분집합이다.
상동은 집합 A와 B에 대하여 A의 모든 원소가 B에 포함되고 B의 모든 원소가 A에 포함되면 A와 B는 상동이다.
𝑨=𝑩 ⇔ 𝑨⊆𝑩 𝒂𝒏𝒅 𝑩⊆𝑨
(2) 분할
하나의 집합을 공지합이 아니면서 서로 중복되지 않은 부분집합들, 즉 서로소인 부분집합들로 나누는 작업을 분할이라고 한다.
분할 결과로서 서로 중복되지 않은 부분집합들이 만들어지게 되는 이들은 쌍으로 서로소가 된다. 간단히는 2개의 집합이 서로소 관계를 가질 수 있고, 나아가서는 n개의 집합이 쌍으로 서로소 관계를 가질 수 있다.
집합 A와 B가 공통된 원소를 가지고 있지 않는다면 서로소라고 하고 다음과 같은 기호로 나타낸다.
𝑨 ∩ 𝑩 = ∅
n 개의 집합 A1, A2, ..., An이 있을 때 서로 같지 않은 임의의 두 집합 Ai와 Aj가 공통된 원소를 가지고 있지 않는다면 쌍으로 서로소라고 하고, 다음과 같이 나타낼 수 있다.
i ≠ j 일 때, 𝑨𝒊∩𝑨𝒋=∅
집합 𝑷 = {𝑨𝟏,𝑨𝟐,⋯,𝑨𝒏}이 집합 A의 분할
⟺
(1) ⋃_{i=1}^n A_i = A and
(2) ⋂_{i=1}^n A_i = ∅
(3) 멱집합 (power set)
집합 A의 모든 부분집합들의 집합을 A의 멱집합이라고 하고, P(A)로 표기한다.
멱집합의 원소 수 | S | = n 은 | P(S) | = 𝟐^𝒏 이다.
2. 집합 연산
(1) 합집합
𝑨 ∪ 𝑩 = {𝒙 ∈ 𝑼 |𝒙 ∈ 𝑨 ∨ 𝒙 ∈ 𝑩}
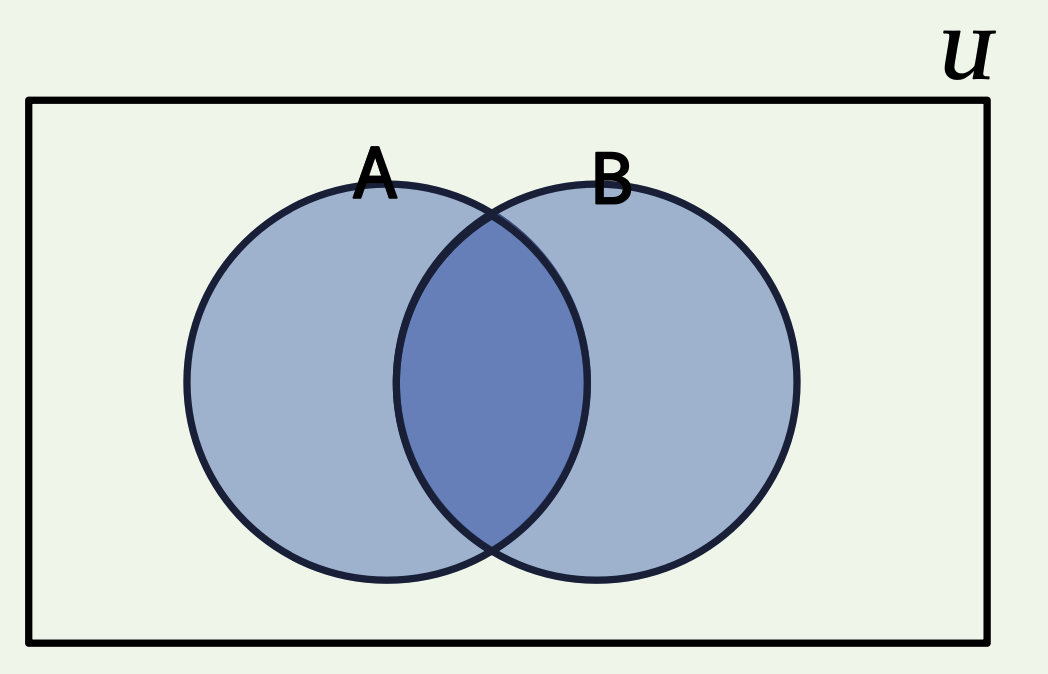
(2) 교집합
𝑨 ∩ 𝑩 = {𝒙 ∈ 𝑼 | 𝒙 ∈ 𝑨 ∧ 𝒙 ∈ 𝑩}
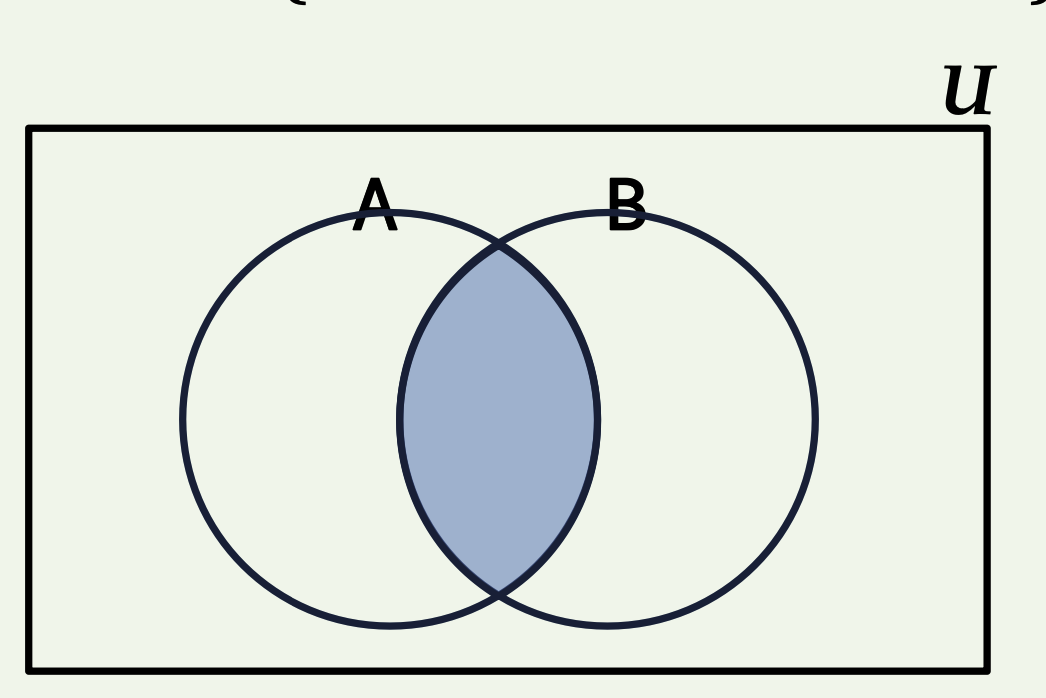
(3) 차집합
A에 속하지만 B에는 속하지 않는 원소의 집합을 A에서 B를 뺀 차집합이라고 한다.
𝑨 − 𝑩 = {𝒙 ∈ 𝑼 | 𝒙 ∈ 𝑨 ∧ 𝒙 ∉ 𝑩}

(4) 여집합 (보집합)
전체집합 U에 속하면서 A에 속하지 않는 원소의 집합을 A의 여집합이라고 한다.
𝑨^𝒄 = 𝑼−𝑨 = {𝒙 ∈ 𝑼 | 𝒙 ∉ 𝑨}

(5) 대칭차집합
전체집합 U가 있고 집합 A와 B가 U의 부분집합일 때, A ∪ B 에속하지만 A ∩ B에 속하지 않는 원소의 집합을 A와 B의 대칭차집합이라고 한다.
𝑨⨁𝑩 = { 𝒙∈𝑼 | 𝒙 ∈ 𝑨 ∪ 𝑩 ∧ 𝒙 ∉ 𝑨 ∩ 𝑩}
(6) 곱집합
𝑼 를 전체집합, 𝑨 ⊂ 𝑼, 𝑩 ⊂ 𝑼라 할 때 𝑨의 원소 𝒂와 𝑩의 원소 𝒃로 만들어지는 순서쌍 (𝒂, 𝒃)들의 집합을 𝑨와 𝑩의 곱집합이라고 한다.
𝑨×𝑩 = { (𝒂, 𝒃) | 𝒂∈𝑨 , 𝒃∈𝑩 }
3. 집합의 대수 법칙
(1) 집합의 크기에 관한 성질
정리 1 합집합의 크기
집합 A, B가 유한집합이면 다음이 성립한다.
| 𝑨∪𝑩 | = | 𝑨 | + | 𝑩 | − | 𝑨 ∩ 𝑩 |
증명: 합집합의 크기에 대한 정리는 유한집합 A와 B에 대해 |A∪B| = |A| + |B| - |A∩B|가 성립한다는 것이다. 이는 A와 B에서 중복되는 원소들을 제외한 나머지 원소들의 전체 수를 나타낸다. 정리의 증명은 A∪B = A∪(B-A)로 표현할 수 있으며, A와 B-A는 서로 공통 원소가 없으므로, 그 크기는 각각의 집합 크기의 합과 같다. 또한, B = (B-A)∪(A∩B)와 같이 표현되고 이 두 집합 역시 서로소이므로 B의 크기는 B-A와 A∩B의 크기 합과 같다. 이를 종합하면 주어진 정리가 증명된다.
따름정리
집합 A, B, C가 유한집합이면 |𝑨 ∪ 𝑩 ∪ 𝑪 | = | 𝑨 | + | 𝑩 | + | 𝑪 | − | 𝑨∩𝑩 | − | 𝑨∩𝑪 | − | 𝑩∩𝑪 | + | 𝑨∩𝑩∩𝑪 |

정리 2 서로소인 집합의 합집합의 크기
집합 A, B가 유한 집합이면서 서로소이면 | A ∪ B | = | A | + | B |
(2) 포함관계 및 항등식
교집합, 합집합, 포함관계의 이행성
모든 집합 A, B, C에 대해서 다음을 만좁한다.
교집합
1. (𝑨∩𝑩) ⊆𝑨
2. (𝑨∩𝑩) ⊆𝑩
합집합
1. 𝑨⊆(𝑨∪𝑩)
2. 𝑩⊆ 𝑨∪𝑩
이행성
만약 𝑨 ⊆ 𝑩이고 𝑩 ⊆ 𝑪 이면, 𝑨 ⊆ 𝑪 이다.
원소 논증
집합의 다양한 대수법칙을 증명하는 가장 기본적인 방법중 하나는 원소 논증을 이용하는 것이다. 원소 논증이란 하나의 집합이 다른 집합의 부분집합임을 증명하기 위해 원소의 포함관계를 이용하는 증명방식이다. 원소 논증의 방법은 다음과 같다.
집합 X와 Y가 주어지고 X ⊆ Y 임을 증명하고자 한다면, X의 임의의 원소 x에 대해서 항상 x ∈ Y가 만족함을 보인다.
집합의 대수법칙
U를 전체집합이라고 할 때 모든 집합 A, B, C에 대해서 다음을 만족한다.
(1) 교환법칙
(a) 𝑨 ∪ 𝑩 = 𝑩 ∪ 𝑨
(b) 𝑨 ∩ 𝑩 = 𝑩 ∩ 𝑨
(2) 결합법칙
(a) (𝑨 ∪ 𝑩) ∪ 𝑪 =𝑨 ∪ (𝑩 ∪ 𝑪)
(b) (𝑨 ∩ 𝑩) ∩ 𝑪 =𝑨 ∩ (𝑩 ∩ 𝑪)
(3) 분배법칙
(a) 𝑨 ∪ (𝑩 ∩ 𝑪) = (𝑨 ∪ 𝑩) ∩ (𝑨 ∪ 𝑪)
(b) 𝑨 ∩ (𝑩 ∪ 𝑪) = (𝑨 ∩ 𝑩) ∪ (𝑨 ∩ 𝑪)
(4) 항등법칙
(a) 𝑨 ∪ ∅ = 𝑨
(b) 𝑨 ∩ 𝑼 = 𝑨
(5) 보수법칙
(a)𝑨∪𝑨^𝒄 =𝑼
(b)𝑨∩𝑨^𝒄 =∅
(6) 이중보수법칙
(a) (𝑨^𝒄)^𝒄 = 𝑨
(7) 멱등법칙
(a) 𝑨 ∪ 𝑨 = 𝑨
(b) 𝑨 ∩ 𝑨 = 𝑨
(8) 전체한계법칙
(a) 𝑨 ∪ 𝑼 = 𝑼
(b) 𝑨 ∩ ∅ = ∅
(9) 드모르간의 법칙
(a) (𝑨 ∪ 𝑩)^𝒄= 𝑨^𝒄 ∩ 𝑩^𝒄
(b) (𝑨 ∩ 𝑩)^𝒄= 𝑨^𝒄 ∪ 𝑩^𝒄
(10) 흡수법칙
(a) 𝑨 ∪ (𝑨 ∩ 𝑩) = 𝑨
(b) 𝑨 ∩ (𝑨 ∪ 𝑩) = 𝑨
(11) 𝑼와 ∅의 여집합
(a) 𝑼^𝒄 = ∅
(b) ∅^𝒄 = 𝑼
(12) 차집합법칙
𝑨 − 𝑩 = 𝑨 ∩ 𝑩^𝒄
포함관계에 대한 동치
U가 전체집합이고 집합 A와 B가 있을 때, 다음 조건 중 하나가 참일 때 나머지 다른 조건도 모두 참이 되고, 다음 조건 중 하나가 거짓이라면 나머지 다른 조건도 모두 거짓이 된다. 즉, 다음 조건들은 모두 동치이다.
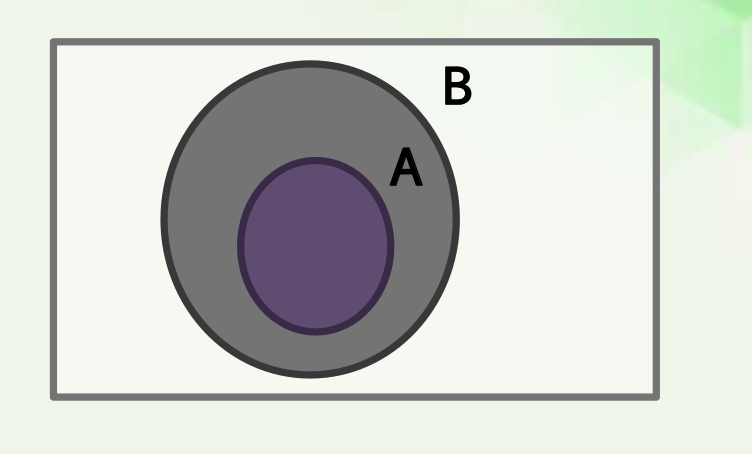
(1) 𝑨⊆𝑩
(2) 𝑩^𝒄 ⊆𝑨^𝒄
(3) 𝑨 ∪ 𝑩 = 𝑩
(4) 𝑨 ∩ 𝑩 = 𝑨
(5) 𝑨^𝒄 ∪𝑩=𝑼
(6) 𝑨∩𝑩^𝒄 =∅
(7) 𝑨 − 𝑩 = ∅
예제
1. 집합 A = {a}이고, B = {a, {a}}라고 하자.
1) A는 B의 부분집합인가?
2) A는 B의 진부분집합인가?
풀이:
1) A는 하나의 원소 a를 가지고 있는 집합이고, B는 a와 {a}를 원소로 가지는 집합이다. A의 모든 원소가 B에 포함되므로 A⊆B이다.
2) A⊆B이면서 A≠B이므로 A는 B의 진부분집합이다.
2. 다음 중 참인 것은?
1) a ⊆ { a, b, c }
2) ∅ ⊆ 𝟏,𝟐,𝟑
3) { 𝟏,𝟑 } ⊆{𝟏,𝟐,𝟑 }
4) {𝟐} ∈ {{𝟏},{𝟐}}
풀이:
1) F -> a는 { a, b, c }의 원소이므로 a ∈ { a, b, c } 로 표현되어야 한다.
2) T -> ∅ 은 모든 집합의 부분집합이므로 참이다.
3) T -> {1,3}의 원소인 1,3은 { 1, 2, 3} 의 원소가 되므로 참이다.
4) T -> 집합 { 2} 는 집합 { { 1 } , { 2 } } 의 원소이므로 참이다.
3. 집합 A의 부분집합 A1 = {1, 2, 4}, A2 = {3, 5}, A3 = {2, 6} 이 있다고 할 때, A1과 A2는 서로소인 집합인가? A2와 A3는 서로소인 집합인가? A1, A2, A3는 쌍으로 서로소인 집합인가?
풀이: A1 ∩ A2 = ∅ 이므로 A1과 A2는 서로소이다. A2 ∩ A3 = ∅ 이므로, A2와 A3는 서로소이다. A1 ∩ A3 = {2} 이므로 A1, A2, A3는 쌍으로 서로소인 집합이 아니다.
4. 집합 {a, b, c}의 모든 분할을 구하시오.
풀이:
{ {a}, {b}. {c} }
{ {a, b}, {c} }
{ {a, c}, {b} }
{ {a}. {b, c} }
{ {a, b, c} }
5. 𝒁가 모든 정수의 집합일 때 𝒁𝟎 = {𝒛 | 𝒛=𝟐𝒌, 𝒌는정수}, 𝒁𝟏 = {𝒛 | 𝒛 = 𝟐𝒌+𝟏 ,𝒌는 정수} 라면, {𝒁𝟎, 𝒁𝟏}은 𝒁의 분할인가?
풀이:
- 𝒁𝟎 ∪ 𝒁𝟏 = 𝒁
- 𝒁𝟎 ∩ 𝒁𝟏 = ∅
∴ {𝒁𝟎, 𝒁𝟏}은 𝒁의 분할이다.
6. 집합 S = {a, b, c}일 때, S의 멱집합 P(S)을 구하시오.
P(S) = { ∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} }
7. 전체집합 U = {1, 2, 3, 4, 5}이다. A={1, 2, 3}, B={2, 3, 4}일 때 𝑨∪𝑩, 𝑨∩𝑩, 𝑨−𝑩, 𝑨^𝒄을구하시오.
풀이: 전체집합 U는 {1, 2, 3, 4, 5}로 주어지고, 집합 A는 {1, 2, 3}, 집합 B는 {2, 3, 4}이다. A와 B의 합집합 A∪B는 각 집합의 모든 원소를 포함하므로 {1, 2, 3, 4}이다. 교집합 A∩B는 A와 B에 공통으로 속하는 원소인 {2, 3}이다. 차집합 A−B는 A에 속하면서 B에는 속하지 않는 원소를 찾으므로 {1}이다. 여집합 A^c는 전체집합 U에서 A의 원소를 제외한 원소로 {4, 5}이다.
8. 𝑨= { 𝟏,𝟐,𝟑 } ,𝑩= { 𝟐,𝟑,𝟒 } 일때 𝑨⨁𝑩를 구하시오.
집합 A와 B의 대칭차집합 A⨁B는 A와 B의 합집합에서 교집합을 제외한 요소로 구성된다. A = {1, 2, 3}, B = {2, 3, 4}의 교집합은 {2, 3}이다. 합집합은 {1, 2, 3, 4}이므로, 교집합인 {2, 3}을 제외한 {1, 4}가 A⨁B의 결과이다. 이 결과를 통해 대칭차는 각 집합에만 속한 고유 요소들로 이루어진 집합임을 알 수 있다.
참고자료: 이산수학 | 손진곤 (지은이) 한국방송통신대학교출판문화원
'CS > 이산수학' 카테고리의 다른 글
| 이산수학 - 함수, 함수의 상등, 전사함수, 단사함수, 합성함수, 계승함수, 바닥함수, 천장함수, 나머지 함수 (0) | 2024.05.15 |
|---|---|
| 이산수학 - 관계, 관계의 표현, 관계의 성질, 관계의 종류, 반사적, 대칭적, 추이적, 동치관계 (0) | 2024.05.15 |
| 이산수학 - 행렬: 행렬의 연산, 종류, 정방행렬, 단위행렬, 역대칭행렬, 삼각행렬, 역행렬, 부울행렬 (0) | 2024.05.15 |
| 이산수학 - 증명, 직접증명법, 수학적 귀납법, 간접증명법, 다양한 증명방법 (0) | 2024.05.13 |
| 이산수학 논리 - 명제, 논리 연산, 술어 논리, 추론 (0) | 2024.05.02 |

