1. 카르노 도표를 이용한 간소화
카르노 도표(Karnaugh map)
- 카르노 도표는 여러 개의 사각형으로 된 다이어그램
- 사각형은 각각 하나의 최소항 또는 최대항을 의미
- 최소항 또는 최대항들이 차지하는 도표 내의 면적을 이용하여 간소화
- 카르노 도표는 부울함수의 입력변수의 수에 따라 기본 도표의 형태가 결정
- 입력 변수의 수가 n인 경우, n 변수 카르노 도표라고 하고 2^n의 사각형으로 구성
카르노 도표를 이용하면
- 정규형 부울함수 => 표준형 부울함수
즉, 1) 최소항의 합 형태나 2) 최대항의 곱 형태로 간소화 된다.
1) 최소항의 합형을 곱의 합형으로 간소화하는 순서
i) 입력변수의 수 n 에 따라 n 변수 카르노 도표 작성(도표는 2^n개의 정사각형)
ii) 최소항의 인덱스에 대응되는 사각형을 1 로 표시
iii) 1 로 표시된 사각형들 중 서로 인접한 사각형끼리 묶음 (이때 한 묶음은 크게, 전체 묶음의 수는 적게)
iv) 각 묶음이 입력변수 각각에 대해 도표상의 어떤 위치에 있는지 파악
(만일 해당 묶음이 입력변수 X에대해 X=1인 곳에만 존재하면
곱항에 X를 남기고, X=0인 곳에만 존재하면 곱항에서 ~X를남긴다.
만일 묶음이 x=0인곳과 x=1인 곳에 걸쳐서 존재한다면 곱항에서 x변수를 소거한다)
v) iv에서 구한 각 묶음에 대한 곱항들을 논리합(OR)으로 연결시키면 간소화된 표준형(곱의 합형)이 구해진다.
2) 최대항의 곱형을 합의 곱형으로 간소화하는 순서
i) 입력변수의 수 n 에 따라 n 변수 카르노 도표 작성(도표는 2^n개의 정사각형)
ii) 최소항의 인덱스에 대응되는 사각형을 0 으로 표시
iii) 0으로 표시된 사각형들 중 서로 인접한 사각형끼리 묶음 (앞의 3과정과 동일-한 묶음은 크게, 전체 묶음의 수는 적게)
iv) 각 묶음이 입력변수 각각에 대해 도표상의 어떤 위치에 있는지 파악
(만일 해당 묶음이 입력변수 X에대해 X=1인 곳에만 존재하면
곱항에 ~X를남기고, X=0인곳에만 존재하면 합항에서 X를남긴다.
만일 묶음이 X=0인곳과 X=1인 곳에 걸쳐서 존재한다면 합항에서 X변수를 소거한다)
v) iv)에서 구한 각 묶음에 대한 합항들을 논리곱(AND)으로 연결시키면 간소화된 표준형(합의 곱형)이 구해진다.
인접사각형이란?
->“두 정사각형에 대응되는 각 최소항(또는 최대항)의 구성변수 중
다른 모든 변수는 동일하되 오직 하나의 변수만 서로 보수관계에 있을 때 두 정사각형은 서로 인접한다” 라고 정의
0 1
0 ~X~Y ~XY
1
~X~Y와 ~XY를 보면 Y에 대해서 하나는 정상형, 하나는 보수형이므로 인접한다.
예를 들어 입력변수 X, Y, Z 3개의 경우
최소항 m4 = X~Y~Z와 m6 XY~Z는 Y, ~Y 하나만 보수를 만족 하므로 인접한다.
카르노 도표를 보면 시각적으로 위/아래, 오른쪽/왼쪽을 바로 인접하는지를 판단할 수 있다.
시각적으로 본 것을 따져보았더니 이러한 원리가 있더라.
대각으로는 인접해있다고 하지 않는다.
인접하는 사각형을 묶기 = 카르노 도표를 통한 간소화에서 가장 중요한 부분
i) 한 묶음 내의 정사각형의 수는 2^n개가 되도록 묶는다.
ii) 한 묶음은 크게, 전체 묶음의 수는 적게 묶는다.
2. 2,3,4 변수의 카르노 도표
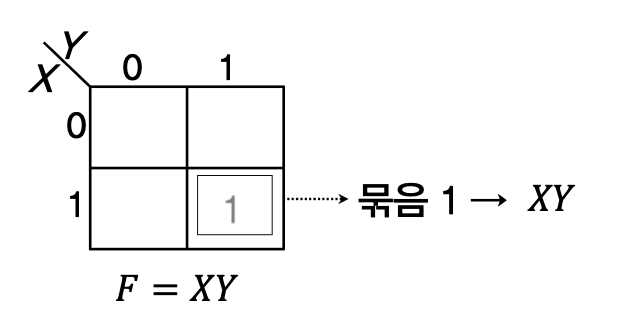
두 개의 변수를 가지는 부울함수 -> 4개의 최소항
- 2변수 카르노 도표는 4개의 정사각형으로 구성되고
- 각각의 정사각형은 하나의 최소항에 대응

다음과 같은 진리표에 대해서
X Y F
0 0 0
0 1 0
1 0 0
1 1 1
=> OR 결합으로 따지므로 0은 의미가 없다
따라서 묶음은 (2,2) 하나만 발생
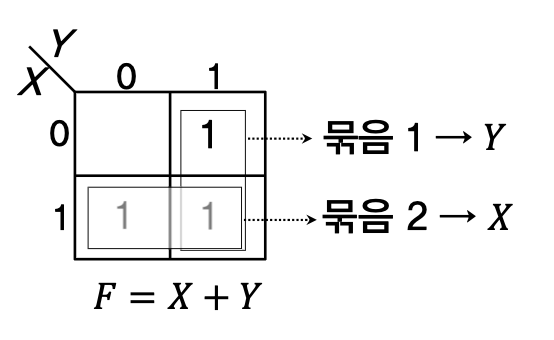
X Y F
0 0 0
0 1 1
1 0 1
1 1 1
=> 이 경우 묶음이 2개가 나온다.
3개의 변수의 경우 다음과 같이 카르노 도표를 그린다.

인접 여부 설정을 위해서 11과 10을 바꿔준 것에 주의해야 한다.
F(X, Y, Z) = ∑(0,1,2,6)의 간소화는 ?
1) 3변수 기본 도표를 작성한다.
2) 주어진 부울함수에서 최소항을 해당 사각형에 1 로 표기한다.
3) 묶는 규칙을 고려하여 인접 사각형끼리 묶는다.
4) 간소화된 각 항을 논리합(OR)으로 결합한다

첫번째 묶음 ~X~Y (Z는 판단할 수가 없으므로)
두번째 묶음 Y~Z
두개를 묶어서

다음 진리표를 갖고 간소화된 논리회로도를 작성해보자.

∑m(0, 2, 4, 6, 7)
=> 카르노도표를 그려보면
A\BC 00 01 11 10
0 1(m0) 1(m2)
1 1(m4) 1(m7) 1(m6)
묶음의 수는 적을 수록 좋기 때문에 하나의 묶음을 최대 크게 묶는다
즉 (1,1) (1,2) (1,4) (2,4) 4개의 사각형을 하나로 묶고, (2,3) (2,4)를 하나로 묶는다
따라서 AB + ~C

참고자료: 디지털논리회로(김형근, 손진곤 공저, KNOU press 출판)
'CS > 디지털논리회로' 카테고리의 다른 글
| 4변수 카르노 도표, 무관 조건, 기타 카르노 도표, NADN 게이트와 NOR 게이트를 이용한 논리회로 구현 (0) | 2023.06.14 |
|---|---|
| 조합논리회로의 분석과 설계, 기본 연산회로, 가산기, 감산기, 가감산기 (0) | 2023.06.14 |
| 부울함수의 정규형 및 표준형, 최소항의 합, 최대항의 곱 (0) | 2023.06.14 |
| 논리연산, 논리 게이트, 부울 대수, 대수적 간소화 (0) | 2023.06.14 |
| 디지털 시스템, 컴퓨터 구성, 집적회로, 수치 데이터, 디지털 코드 (0) | 2023.06.14 |



