부울함수가 어떻게 유도되는지를 살펴본다.
1. 정규형
- 부울 함수를 최소항의 합(Sum of Minterm) 이나 최대항의 곱(Product of Maxterm) 으로 표현한 것
최소항과 최대항
- 2개의 논리 변수 X, Y가 있을 때
-> 최소항: 논리곱 (AND)로 표현되는 XY, X~Y, ~XY, ~X~Y의 네가지 항(그 결과가 논리 -> 1)
X Y
0 0 -> ~X~Y
0 1 -> ~XY
1 0 -> X~Y
1 1 -> XY
이렇게 네개의 항이 만들어지는데 그 결과가 논리 1값을 가지는 것
=> 최소항의 개념은 그 변수의 결합이 1이라는 것
즉 00을 가진 변수가 1값을 가지려면 ~X~Y이어야 한다.
-> 최대항 : 최소항의 쌍대 : 논리합(OR)로 표현되는 결과가 논리 0
X + Y, ~X + Y, X + ~Y, ~X + ~Y의 결과가 0이다.
따라서 최소항을 알게되면 최대항을 알고 그 반대도 마찬가지.
입력변수 3개에 대해서 총 2진값의 총 조합은 8개이다.

예를 들어 0 0 0 을 보면 최소항이 되려면 1이 나와야 하고 곱으로 연결되므로 모두 보수를 취해야 한다.
1 0 0 을 보면 최소항이기 위해서는 Y가 ~Y로, Z가 ~Z로 되어야 한다.
1 1 0을 보면 최대항이 되기 위해서는 X =0, Y = 0, Z = 0 이어야 하므로 ~X, ~Y를 취해주고 더하기로 연결한다.
입력변수에 따라 최소항과 최대항을 쉽게 알 수 있으려면
m1 => 0 0 1 = ~X~YZ
1) 최소항
n 개의 논리변수로 구성된 부울함수에서 최소항이란 ?
- 각 변수의 문자 1개씩 모두 n 개의 논리곱으로 표시
- 그 결과가 논리 1인 경우
- mj로 표현한다.
2) 최대항
n 개의 논리변수로 구성된 부울함수에서 최대항이란?
- 각 변수의 문자 1개씩 모두 n 개의 문자의 논리합 항으로서
- 그 결과가 논리 0 인 경우
- Mj 로표시
그렇다면 최소항과 최대항은 부울함수와 어떤 연관을 갖는가?
진리표 : 입력과 출력 => 2진수 표로 만들어놓은 것
부울함수는 최소항 or 최대항 둘 중 하나로 표현한다.
만약 어떤 함수가 최소항으로 표현되었다고 한다면 => OR 결합으로 되었다는 것을 의미
따라서 다음과 같은 진리표에 대해서 최소항을 표현한다면 다음과 같다.
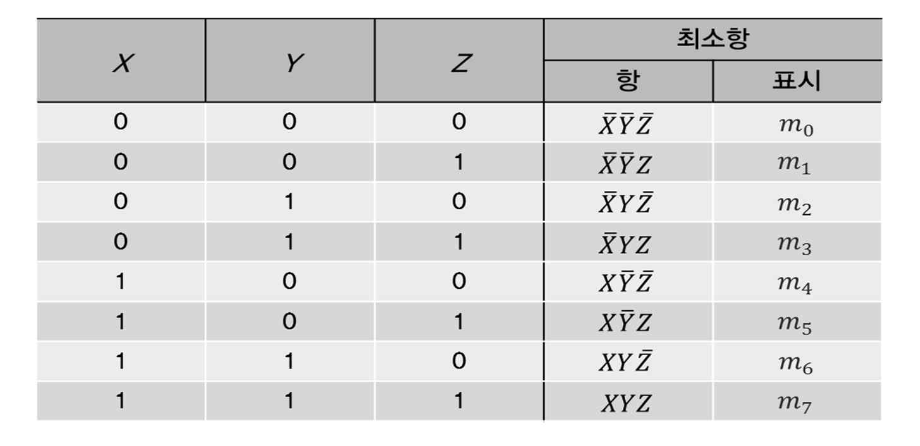
8개 경우의수를 8개의 합 형태로 표현해주자.
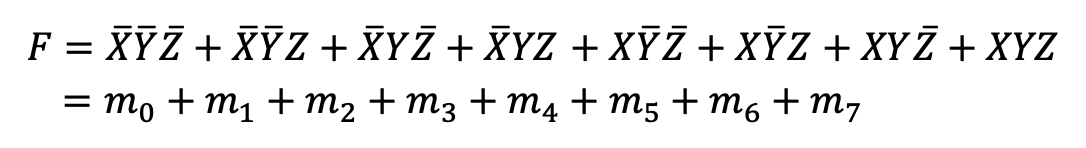
시그마로 표현한다면 다음과 같다.
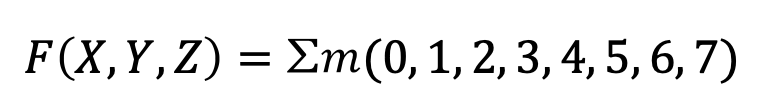
마찬가지로 곱 형태로 표현하면 최대항의 표현이 된다.
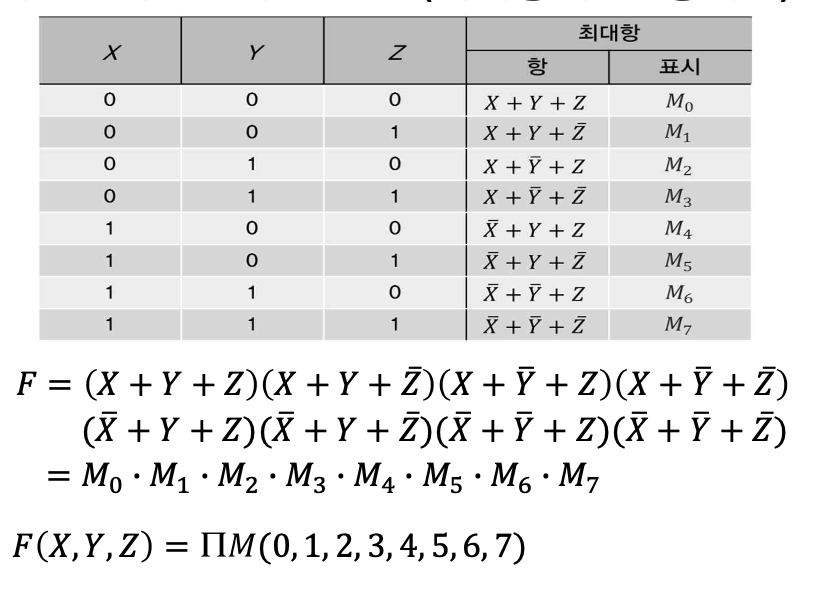
최소항의 합으로 부울함수를 표현해보자.
-> 진리표에서 출력이 1이 되는 최소항들을 논리합 OR로 묶는다
=> 정규형 부울함수
다음과 같은 진리표에 대해서 8개 조합이 만들어지는데, 최소항의 표현은 1인 것만 찾아도 된다.
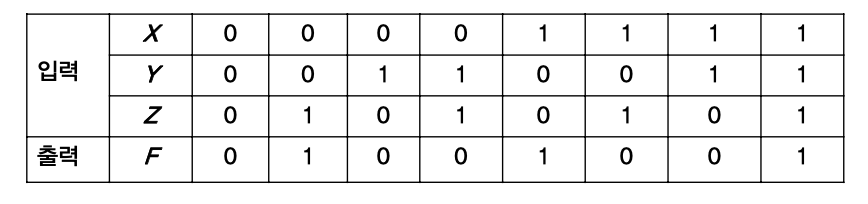
최소항, 즉, 출력 F가 1이 되기 위해서는 0 0 1, 1 0 0, 1 1 1 중 하나이면 된다.
따라서 1인 것만 찾아서
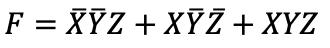
왜 정규형이냐 ? 표준형은 이러한 것들을 좀 더 간소화된 형태로 나타낸다.
정규화된 부울함수와 표준형 부울함수의 관계
다음과 같이 간소화된 표현이 결국 정규형에서 나온 것이라고 이해하면 된다.
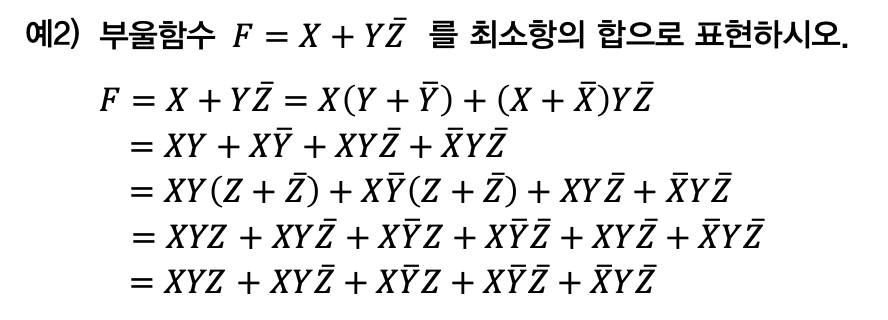
마찬가지로 최대항의 표준형과 정규형도 다음과 같이 표현할 수 있다.

진리표를 갖고 최대항을 표현해보자.
=> 곱으로 연결이 되어 있어야 하며 출력이 0이어야 한다.
즉 진리표에서 0만 구하면 된다
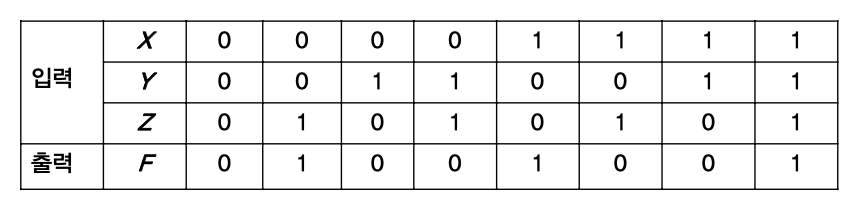
000, 010, 011, 101, 110 을 곱으로 표현
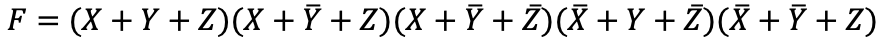
2. 표준형
표준형
- 부울함수를 표현하는 간소화된 형태 (정규형은 모든 입력 변수가 다 포함되어 있다.)
-> 소거가 되어 있는 형태
표준형도 곱의 합이나 합의 곱으로 표현이 되어 있다.
1) 곱의 합
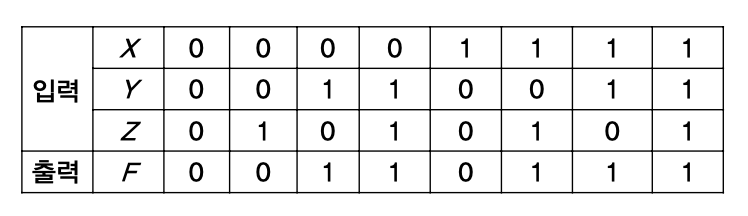
정규형을 구하고 간소화를 통해 구한다.
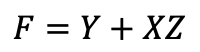
표준형 곱의 합으로 표현된 F = ~Y + ~XY~Z + XY의 논리회로도를 표현하면 다음과 같다.
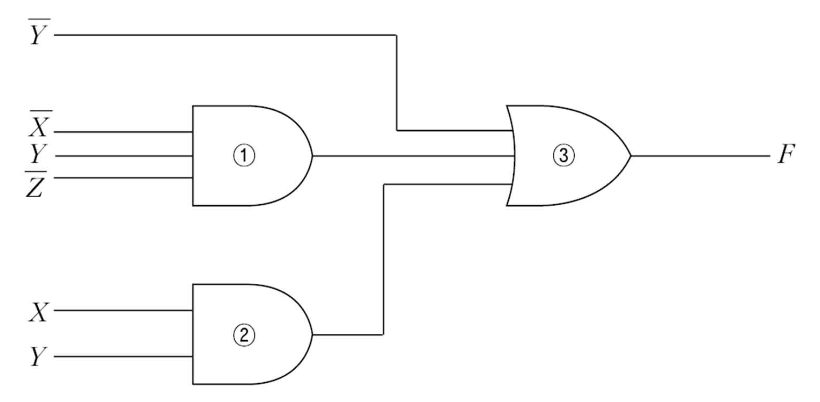
왜 곱의 합이어야 할까?
하나로 묶은 다음에 3번처럼 한번에 처리할 수 있다.
=> 하나의 OR 게이트와 여러 개의 AND 게이트

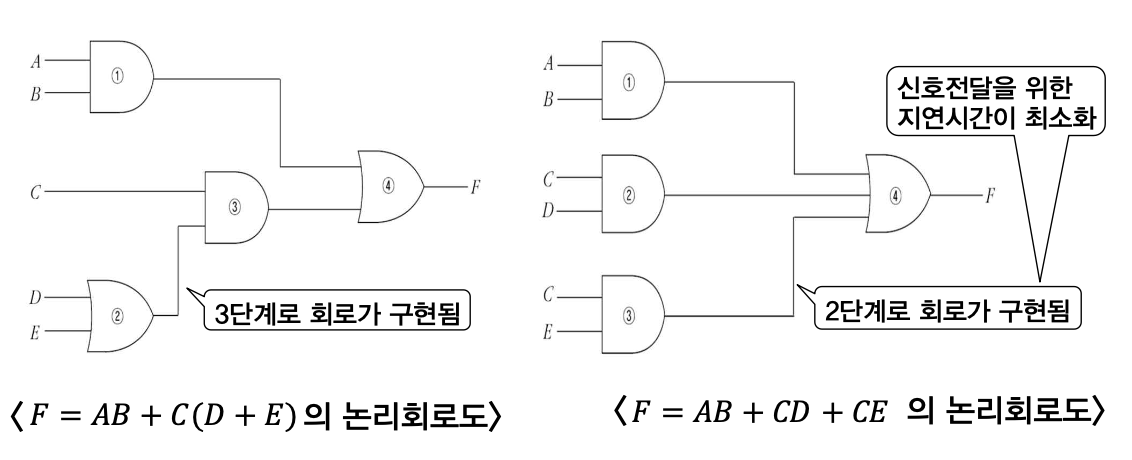
첫 번째 식은 곱의 합 형태가 아니다. 왜냐하면 항 (D+E)는 합의 형태이지 단일 변수가 아니기 때문.
괄호를 제거해서 두 번째 식처럼 만들어주어야 한다.
소자의 개수는 차이가 없지만 입력이 들어왔을 때 단계가 다르다.
입력 -> 출력까지 도달하는 단계가 첫 번째는 3단계, 두 번째는 2단계
=> 훨씬 효율적이다.
참고자료: 디지털논리회로(김형근, 손진곤 공저, KNOU press 출판)
'CS > 디지털논리회로' 카테고리의 다른 글
| 4변수 카르노 도표, 무관 조건, 기타 카르노 도표, NADN 게이트와 NOR 게이트를 이용한 논리회로 구현 (0) | 2023.06.14 |
|---|---|
| 조합논리회로의 분석과 설계, 기본 연산회로, 가산기, 감산기, 가감산기 (0) | 2023.06.14 |
| 부울함수의 간소화, 카르노 도표 (0) | 2023.06.14 |
| 논리연산, 논리 게이트, 부울 대수, 대수적 간소화 (0) | 2023.06.14 |
| 디지털 시스템, 컴퓨터 구성, 집적회로, 수치 데이터, 디지털 코드 (0) | 2023.06.14 |



