1. 디지털 시스템
검은 상자형 시스템
- 입력과 출력을 갖는 검은 상자로 표현
- 시스템의 입력과 출력에만 관심
구성요소 집합으로서의 시스템
- 검은 상자 내부에 관해 규정
- 시스템에 부여된 목적을 달성하기 위해 상호작용하는 구성요소들의 집합
데이터 표현 방법
- 아날로그 방식: 데이터를 연속적인 값으로 표현
- 아날로그 시스템: 입력과 출력이 아날로그 데이터임(전압의 변이 등이 표현된 계기 시스템)
- 디지털 방식: 연속적인 값을 간사하여 이산적인 값으로 표현
- 디지털 시스템: 입력과 출력이 디지털 데이터인 시스템(디지털 시계, 디지털 온도계 등)
디지털 시스템의 장점
- 편리성
- 융통성
- 단순성
- 안정성
- 견고성
- 정확성
디지털 시스템의 설계
회로 설계 -> 논리 설계 -> 시스템 설계 -> 실제적 설계
디지털 논리회로란?
- 2진 디지털 논리를 논리 게이트로 구현
- 디지털 시스템을 구현하는 기본 요소
- 디지털 시스템의 논리설계 단계에서 설계됨
디지털 논리회로는 저장 요소의 유무에 따라
-> 조합논리회로 (저장 요소가 없음: 가산기, 디코더 등)
-> 순서논리회로 (저장 요소가 있음: 레지스터, 카운터 등)
으로 구분된다.
2. 컴퓨터 구성
1) 컴퓨터 시스템
전자식 데이터 처리 시스템
- 컴퓨터를 시스템 측면에서 분석
- 무엇으로 구성되어 있는가, 요소는 각각 무슨 기능인가, 입출력은 무엇인가
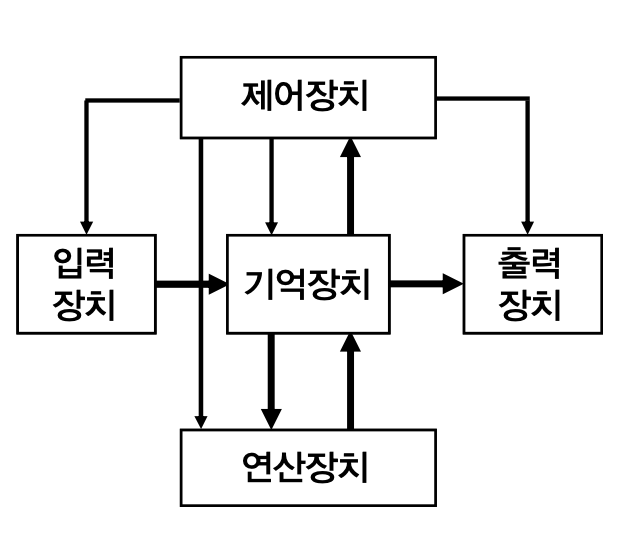
2) 컴퓨터 하드웨어의 구성
- 입력장치
- 기억장치
- 연산장치
- 제어장치
- 출력장치
3. 집적회로
1) 집적회로의 개요
디지털 논리회로는 집적회로로 구성
집적회로란?
Integrated Circuits
- 디지털 게이트의 기능을 수행하는 전자소자를 포함한 작은 실리콘 반도체 크리스털
- chip이라고 함
- 칩 내부에 있는 여러 가지 게이트들은 회로의 목적에 부합되도록 상호 연결
2) 집적도
집적도
- 단위 실리콘 칩에 집적할 수 있는 게이트의 수
- 소규모(SSI)
- 중규모(MSI: Medium Scale Integration) : 대략 10 ~100여 개의 게이트를 내장 (디코더, 레지스터)
- 대규모(LSI): 수백 ~ 수천 개 (프로세서, 기억장치 칩)
- 초대규모
3) 디지털 논리계열
집적회로로 구성
- 기본 회로설계를 공유하는 집적회로의 그룹: 논리계열
- 각 논리 계열의 기본회로는 NAND 게이트 또는 NOR 게이트
4) 양논리와 음논리
게이트의 입력과 출력에 대한 2진 신호는 두 값중 하나의 값
-> 두 논리값(0,1)에 대한 두 신호값을 할당하는 방법

4. 수치 데이터
진법
- 수를 숫자로 나타내는 방법
- 숫자의 위치에 따라 가중치 부여
- 가중치는 기수의 승수(거듭제곱)을 이용
- 기수는 2 이상의 양의 정수
r진법
- 기수가 r인 경우 r진법이라고 함
- r개의 숫자로 표현
- r진법으로 표현된 수를 r 진수라고 함
- r진수 오른쪽 아래에 기수 r을 표시
r진법으로 표현된 r진수 N
10진수 178.510
-> 178.510 = 1×102+7×101+8×100+5×10-1
2진수 1010.012
-> 1010.012 = 1×23+0×22+1×21+0×20+0×2-1+1×2-2 = 8+0+2+0+0+0.25 = 10.2510
진수 변환
1) r 진수의 10진수 변환
- 2진수 1011.101을 10진수로 변환
1011.1012 = 1×23 + 0×22 + 1×21 + 1×20 + 1×2-1 + 0×2-2 + 1×2-3
= 8 + 0 + 2 + 1 + 0.5 + 0 + 0.125
= 11.625
- 8진수 262.3을 10진수로 변환
262.38 = 2×82 + 6×81 + 2×80 + 3×8-1
= 128 + 48 + 2 + 0.375
= 178.375
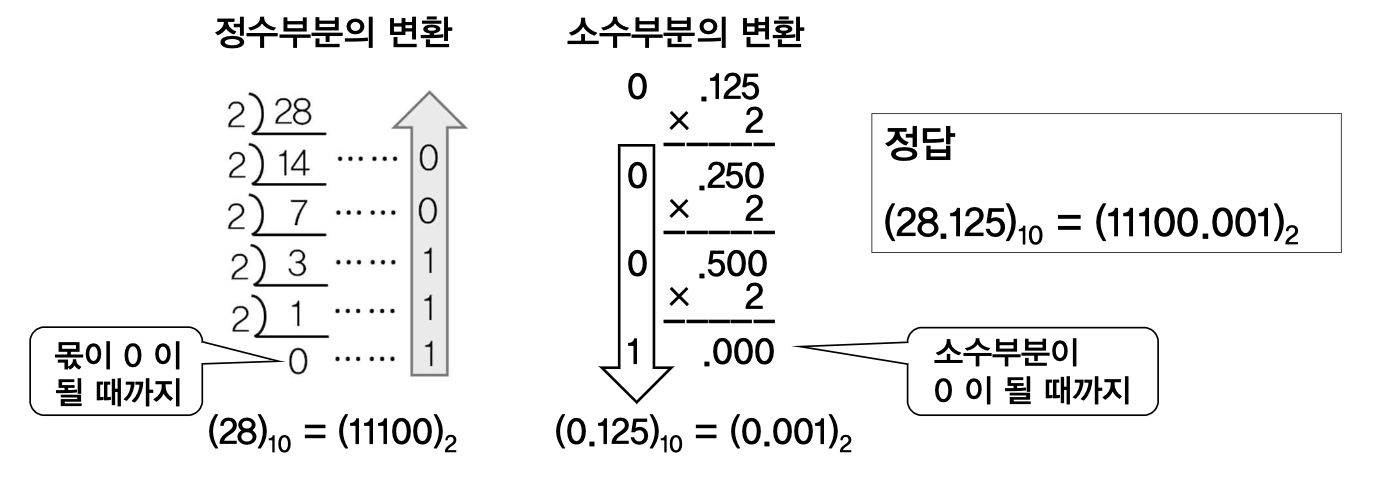
2) 10진수의 r 진수 변환
-> 정수 부분은 나눗셈, 소수점 아랫부분은 곱셉으로 구함
- 10진수 28.125를 2진수로 변환
3) 2진수와 2^n진수의 상호 변환
- 2진수 10110010.011을 각각 4, 8, 16진수로 변환
4진수로 변환:
2진수를 4비트씩 끊어서 각 그룹을 10진수로 변환. 소수점 이하 부분은 그대로 유지.
-> 1011 0010.011
-> 위의 그룹을 10진수로 변환
-> (10진수) 11 2.3
-> 따라서, 2진수 10110010.011은 4진수로는 112.3
8진수로 변환:
2진수를 3비트씩 끊어서 각 그룹을 10진수로 변환. 소수점 이하 부분은 그대로 유지.
-> 10 110 010.011
-> 위의 그룹을 10진수로 변환
-> (10진수) 2 6 2.3
-> 따라서, 2진수 10110010.011은 8진수로는 262.3
16진수로 변환:
2진수를 4비트씩 끊어서 각 그룹을 16진수로 변환. 소수점 이하 부분은 그대로 유지.
-> 1011 0010.011
-> 위의 그룹을 16진수로 변환
-> (16진수) B 2.3
-> 따라서, 2진수 10110010.011은 16진수로는 B2.3
- 8진수 436.71을 2진수로 변환
->2n 진수의 각 자리의 수를 대응하는 n 비트의 2진수로 바꾼다.
-> 이 경우는 n = 3이므로 3비트 2진수로 바꾼다.
100011110.111001
-> 436.718 =100011110.111001
4) 기타 변환(r진수를 s진수로 변환)
-> 먼저 10진수로 변환한다음 다시 s진수로 변환
- 5진수 304.12를 8진수로 변환
먼저, 정수 부분인 304를 10진수로 변환
-> 3 × 5^2 + 0 × 5^1 + 4 × 5^0 = 75
따라서, 5진수 304는 10진수로는 75
다음으로, 소수 부분인 0.12를 10진수로 변환.
-> 1 × 5^(-1) + 2 × 5^(-2) = 0.2
따라서, 5진수 0.12는 10진수로는 0.2
이제 정수 부분과 소수 부분을 합쳐서 10진수로 표현하면 75.2
마지막으로, 10진수인 75.2를 8진수로 변환
-> 정수 부분인 75를 8진수로 변환하면 113
-> 소수 부분인 0.2를 8진수로 변환하면 0.1463
-> 따라서, 5진수 304.12는 8진수로는 113.1463
산술 연산하기
- 가산연산 : (27E)16+(3F4)16을 계산하시오
먼저 두 숫자를 10진수로 바꾸어 10진수 덧셈
그 다음 그 결과를 다시 r진수의 합과 올림수로 반환
| 2 7 14
+ | 3 15 4
_________
끝자리 18 = 16 + 2 => 올림수 1 발생 => (1) 2
두번째자리 23 = 16 + 7 => 올림수 1 발생 => (1) 7
첫자리 2 + 3 = 6
따라서 답은 672
2) 보수
보수란 보충수. 즉 더해서 r이 나오는 것.
1) r의 보수(정수 부분이 n자리 일 때)
==>
10진수 35.3410 의 9의 보수는
102 - 10-2 - 35.34 = 99.99-35.34 = 64.65
2진수 1101.112 의 1의 보수는
2^4 - 2^-2 - 1101.11 = (1111.11-1101.11) = (0010.00)
보수에서 중요한 개념은 r의 보수와 (r-1) 보수의 관계
r의 보수 = r-1의 보수 + 가장 낮은 자리의 1이다.
즉 2의 보수는 1의 보수에 1을 더한 것과 같다.
예1) 10진수 67810의 10의 보수를 구하기 위해 67810의9의보수는103 -100 -678=999–678=321이므로
결국 67810의 10의 보수는 321 + 1 = 322 가 된다.
예2) 2진수 11102의 2의 보수는
1110의 (1의 보수 + 1) 이므로 결국 0001 + 1 = 0010 이 된다.
즉 2진수의 1의 보수는 1을 0으로, 0을 1로 바꾸면 구해진다.
보수를 이용한 감산이 가능하다. 여기서 핵심은 덧셈을 이용해서 뺄셈을 한다는 것이다.
예1) 10진수 감산 923-678인 경우 923-678=245이다.
그러나 보수를 이용한 감산은 678의 10의 보수(=322)를 이용하여 가산을 하면
되므로 923 + 322 = 1245 가 되고 올림수 1을 무시하면 245가 된다.
2진수의 경우에도 마찬가지로
예2) 2진수 감산 (1011)2 - (0101)2 의 경우(보수와 가산을 이용한 2진수 감산)

이와 같은 보수의 개념이 논리회로를 단순하게 만들어 연산을 하게 하는데 핵심 원리가 된다.
5. 디지털 코드
10진수를 나타내는 다양한 2진 코드
- BCD8421
- BCD2421
- Excess-3
- Gray
영숫자 코드
1) ASCII 코드: 7비트로 구성 -> 실제 사용될 때는 1비트의 패리티를 포함하여 8비트 전송
2) EBCDIC 코드: 8비트로 구성 -> 1비트의 패리티 비트를 포함하여 전송하면 9비트가 되어 비효율적
3) 유니코드: 전세계 문자체계 표현
참고자료: 디지털논리회로(김형근, 손진곤 공저, KNOU press 출판)
'CS > 디지털논리회로' 카테고리의 다른 글
| 4변수 카르노 도표, 무관 조건, 기타 카르노 도표, NADN 게이트와 NOR 게이트를 이용한 논리회로 구현 (0) | 2023.06.14 |
|---|---|
| 조합논리회로의 분석과 설계, 기본 연산회로, 가산기, 감산기, 가감산기 (0) | 2023.06.14 |
| 부울함수의 간소화, 카르노 도표 (0) | 2023.06.14 |
| 부울함수의 정규형 및 표준형, 최소항의 합, 최대항의 곱 (0) | 2023.06.14 |
| 논리연산, 논리 게이트, 부울 대수, 대수적 간소화 (0) | 2023.06.14 |



