게임트리
주관식 연습문제
1. 바둑이나 서양장기 등과 같이 상대방이 있는 게임을 진행할 때 다음 둘 수를 결정하기 위한 탐색트리에 대하여 설명하라.
상대방과 대결하는 게임의 경우 나는 내가 둘 수 있는 다음 수 중 내게 가장 유리한 수를 선택하려 할 것이고, 상대방은 내게 가장 불리한 수를 선택하려고 할 것이다. 이러한 관계는 최대최소 트리로 표현되고, 수의 선택은 최대최소 트리를 탐색하여 정할 수 있다.
우선 내게 가장 유리한 수를 선택하는 것은 후계상태 중에서 내게 가장 유리한 상태를 선택하는 것이다. 이것은 후계상태 중 노드의 바람직한 정도('나'를 기준으로)를 나타내는 가치가 가장 큰 것을 선택하는 것이며 이는 최대화 단계에 해당된다. 예를 들어 아래 그림의 'A'에서는 가치가 가장 큰 'C'를 선택한다.
상대방이 둘 차례를 나타내는 상태에서 상대방이 내게 가장 불리한 수를 선택하는 것은 후계상태 중에서 내게 가장 불리한 상태를 선택하는 것이다. 이것은 후계상태 중 노드의 바람직한 정도('나'를 기준으로)를 나타내는 가치가 가장 작은 것을 선택하는 것이며 이는 최소화 단계에 해당된다. 예를 들어 아래 그림의 'E'에서는 가치가 가장 작은 'H'를 선택한다.
탐색트리는 최대화 단계와 최소화 단계가 교대로 일어나는 형태로 구성되며, 이를 최대최소 탐색트리라고 한다.
2. 게임을 위한 최대최소 탐색트리가 다음과 같다고 하자. 리프노드에는 각 노드에서 평가한 리프노드의 가치가 표시되어 있다. a
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[
level 1/.style={sibling distance=30mm},
level 2/.style={sibling distance=15mm}
]
\node {a}
child {node {b}
child {node {f \\ (1)}}
child {node {g \\ (3)}}
}
child {node {c}
child {node {h \\ (9)}}
child {node {i \\ (10)}}
child {node {j \\ (1)}}
}
child {node {d}
child {node {k \\ (6)}}
child {node {l \\ (3)}}
}
child {node {e}
child {node {m \\ (2)}}
child {node {n \\ (15)}}
child {node {o \\ (?)}}
};
\end{tikzpicture}
\end{document}

최소화 단계의 노드인
3. 몬테카를로 트리 탐색 알고리즘을 구성하는 네 단계에 대하여 설명하라.
몬테카를로 트리 탐색 알고리즘은 루트노드 하나만 가지고 있는 트리로 시작하여 다음 네 단계를 반복 실행한다.
① 선택(selection): 루트노드에서 시작하여 선택전략에 따라 자식노드를 선택하는 과정을 깊이방향으로 반복한다. 이 선택과정은 아직 시도해 보지 않은 행동이 남아 있는 노드에 도달할 때까지 반복한다.
② 확장(expansion): 선택된 노드에 새로운 행동을 함으로써 자식노드를 생성해 트리에 추가하여 트리를 확장한다.
③ 시뮬레이션(simulation): 확장된 노드로부터 시작하여 게임이 끝날 때까지 스스로 게임을 진행한다(롤아웃, 플레이아웃). 이 모의게임의 결과는 게임에 따라 정해진 점수일 수도 있고, 승리(+1), 무승부(0), 패배(−1)라는 값이 사용될 수도 있다.
④ 역전파(backpropagation): 시뮬레이션 결과를 확장된 노드로부터 루트노드까지 선택경로를 따라 역전파하여 통계를 업데이트한다.
4. 몬테카를로 탐색과정의 어느 시점에서 다음 그림과 같이 트리가 구성되어 있다. 다음 확장할 노드에 도달하기 위해 루트노드에서 자식노드 중 하나를 선택할 때 n1 n2 Ni ni vi

UCB1은 다음과 같다.
현재의 트리에서 노드
따라서 UCB1이 더 큰 노드
객관식 연습문제
1. 다음 중 최대최소 탐색을 이용한 게임 문제에 대한 설명으로 올바른 것은?
① 1인용 게임을 위한 탐색트리이다.
② 내가 둘 상태를 나타내는 노드에서는 가치가 가장 높은 후계노드를 선택한다.
③ 상대방은 후계노드를 무작위로 선택할 것으로 간주한다.
④ 경험적 지식을 적용한 평가함수가 필요 없다.
정답: 2
해설: 정답은 2이다. 최대최소 탐색은 게임 이론에서 두 명의 플레이어가 번갈아 가며 최선의 수를 선택하여 자신의 승률을 극대화하려는 방법이다. 내가 둘 차례에서는 가능한 모든 수를 고려하여 최상의 결과를 가져오는 후계 노드를 선택한다.
반면, 1번은 최대최소 탐색이 1인용 게임에 국한된다는 잘못된 설명이다. 3번은 상대방이 최악의 수를 선택할 것을 전제로 하지 않아 틀리다. 4번은 평가함수가 없으면 게임의 상태를 적절히 평가할 수 없기 때문에 잘못된 설명이다.
2. 다음 최대최소 탐색트리에서 A의 평가함수와 다음으로 선택할 수는 무엇인가?
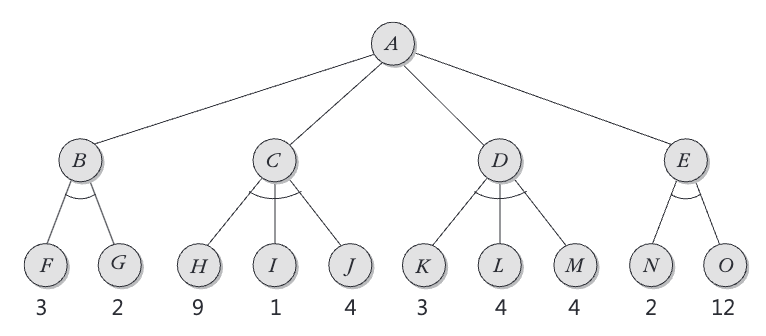
정답: 3, D
해설: 최소화 노드인
3. 다음 최대최소 탐색트리에서
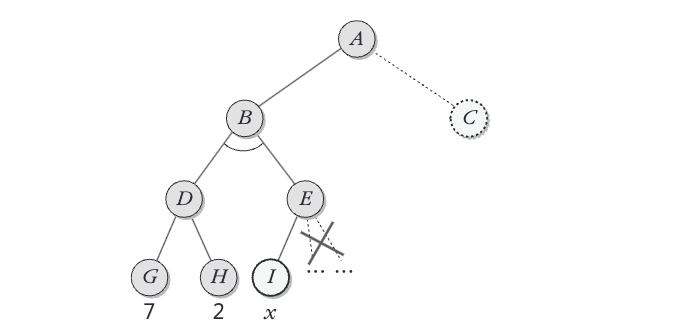
1) 2
2) 4
3) 6
4) 8
정답: 4
해설:
노드
알파-베타 가지치기 과정을 단계별로 설명해보자.
A
/ \
B C
/ \
D E
/| /|\
G H I ...
7 2 x ...
각 노드의 의미:
- 최대화 노드 (Maximizing Node): A, D, E (최대한 큰 값을 선택하려는 노드)
- 최소화 노드 (Minimizing Node): B (최대한 작은 값을 선택하려는 노드)
1. 노드 D의 평가:
- 노드 D의 자식 노드 G와 H의 값은 각각 7과 2.
- D는 최대화 노드이므로, 자식 노드의 최대값을 선택한다:
- 따라서, 노드 D의 값은 7이다.
2. 노드 B의 β 값 갱신:
- B는 최소화 노드이므로 자식 노드의 최소값을 선택
- 현재 노드 B의 자식 노드 D의 값을 기반으로, β 값은 7이다:
3. 노드 E의 평가:
- 노드 E는 최대화 노드로, 자식 노드 H와 I의 값은 각각 2와 x이다.
- E의 자식 노드 중 하나라도 7보다 큰 값을 가지는 경우, B의 선택 가능성이 없어져 가지치기가 발생한다.
- E의 자식 노드 I의 값이
- 따라서
요약
- 최대화 노드 (E)의 경우: 큰 값을 선택하려고 한다.
- 최소화 노드 (B)의 경우: 작은 값을 선택하려고 한다.
- β 값: B의 최소화 노드에서의 최소값으로 7.
- E의 자식 노드 I의 값이
따라서, 문제의 정답은
4. 다음 중 몬테카를로 트리 탐색에 대한 설명으로 올바른 것은?
① 너비우선 탐색 방식에 해당된다.
② 어떠한 상태의 가치를 추정할 수 있는 경험적 평가함수가 필요하다.
③ 탐색과정에서 새로 생성된 노드의 가치를 알아내기 위해 롤아웃을 수행한다.
④
정답: 3
해설: 몬테카를로 트리 탐색에서는 탐색공간을 무작위로 표본화하는 방식으로 탐색트리를 구성한다. 어떠한 상태에 대한 가치를 추정할 때 경험적 지식을 반영한 평가함수를 사용하는 방식이 아니라 탐색공간을 무작위 방식으로 스스로 게임을 끝까지 진행해 보는 몬테카를로 롤아웃을 하는 시뮬레이션에 의해 노드의 가치를 추정하고, 이에 따라 그 노드의 조상노드들의 가치를 정하기 위한 통계치를 업데이트하는 과정을 반복하면서 트리를 구성한다. 이것은 최대최소 탐색처럼 어떠한 상태에 대한 가치를 추정할 때 경험적 지식을 반영한 평가함수를 사용하는 방식이 아니므로 문제영역에 대한 지식이 많지 않아도 된다.
5. 다음 중 몬테카를로 트리 탐색의 선택전략에 대한 적절한 설명은?
① 탐사와 활용 사이의 균형을 이룰 수 있도록 설계한다.
② 자식 중에서 무작위로 하나를 선택한다.
③ 시뮬레이션 결과에 따라 노드들의 통계치를 업데이트하는 처리를 한다.
④ 가장 많이 방문한 자식노드를 선택하는 정책을 사용한다.
정답: 1
해설: 몬테카를로 트리 탐색에서 자식노드 중 하나를 선택할 때에는 탐사와 활용 사이의 균형을 이룰 수 있는 전략을 사용한다. 탐사는 평가의 불확실성으로 인해 아직은 덜 유망한 것으로 보이지만 향후 우수한 것으로 드러날 수 있는 수들을 선택할 수 있도록 하는 것이고, 활용은 지금까지의 결과 중 가장 우수한 결과를 이끌어 내는 수를 선택하는 것이다.
추가 연습문제+
1. 다음 최대최소 탐색 트리의 노드
\documentclass{article}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[
level 1/.style={sibling distance=40mm, level distance=15mm},
level 2/.style={sibling distance=20mm, level distance=15mm},
edge from parent/.style={draw, -latex}
]
\node {a}
child {node {b}
child {node {f \\ (7)}}
child {node {g \\ (1)}}
child {node {h \\ (2)}}
}
child {node {c}
child {node {i \\ (3)}}
child {node {j \\ (4)}}
}
child {node {d}
child {node {k \\ (5)}}
child {node {l \\ (4)}}
}
child {node {e}
child {node {m \\ (2)}}
child {node {n \\ (6)}}
};
\end{tikzpicture}
\end{document}

정답: 3
해설:
최대최소 탐색 트리에서 노드
1. 최종 노드의 값 결정 (리프 노드):
- 리프 노드의 값은 고정되어 있으며, 여기서는 이미 주어진 값이다.
-
2. 최소 노드에서 최소값 선택:
- 최소 노드는 자식 노드들 중에서 가장 작은 값을 선택한다. 이는 상대방이 최적의 방어 전략을 취한다고 가정하는 것이다.
- 노드
-
- 노드
-
- 노드
-
- 노드
-
3. 최대 노드에서 최대값 선택:
- 최대 노드는 자식 노드들 중에서 가장 큰 값을 선택한다. 이는 자신의 최적의 전략을 취하는 것이다.
- 노드
-
따라서, 노드
2. 다음과 같은 최대최소 탐색트리에서
\documentclass{article}
\usepackage{geometry}
\usepackage{tikz}
\usetikzlibrary{trees}
\geometry{a4paper, margin=0.5cm} % 여백을 줄여 페이지에 더 많은 공간 확보
\begin{document}
\begin{tikzpicture}[
scale=0.7, % 트리 크기 축소
level distance=2cm,
level 1/.style={sibling distance=14cm},
level 2/.style={sibling distance=5.5cm},
level 3/.style={sibling distance=1.5cm},
every node/.style={circle, draw, fill=blue!10, minimum size=1cm, inner sep=0pt}
]
\node {}
child {node {A}
child {node {}
child {node {3}}
child {node {6}}
child {node {4}}
}
child {node {}
child {node {2}}
child {node {7}}
child {node {3}}
child {node {5}}
}
}
child {node {B}
child {node {}
child {node {9}}
child {node {3}}
child {node {5}}
}
child {node {}
child {node {1}}
child {node {2}}
}
child {node {}
child {node {7}}
child {node {10}}
child {node {4}}
}
};
\end{tikzpicture}
\end{document}
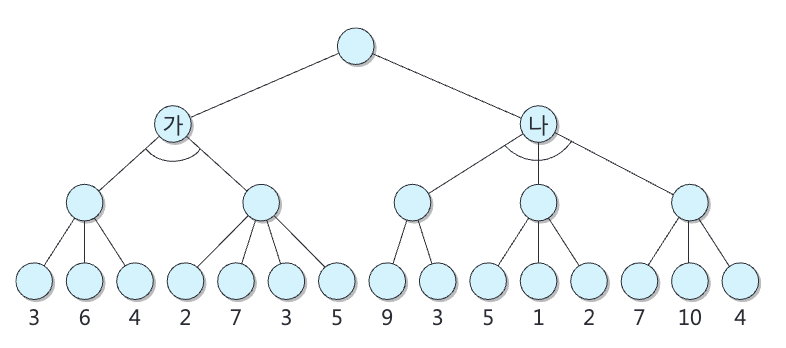
먼저 주어진 트리 구조를 이해해보자. 루트 노드 아래에 두 개의 자식 노드 A와 B가 있으며, 각 자식 노드 아래에는 2단계의 하위 노드가 있다.
루트
/ \
A B
/ \ / \
... ... ... ...
단계별 선택 과정과 가지치기 적용
1. 최대화 노드 (루트 노드):
루트 노드는 최대화 노드이다. 따라서, 자식 노드 A와 B 중 더 큰 값을 선택한다.
2. 최소화 노드 (A와 B):
A와 B는 루트 노드의 자식 노드로 최소화 노드이다. 각 최소화 노드의 자식 노드들 중 최소 값을 선택한다.
3. A 노드의 자식 노드들:
- A의 첫 번째 자식 노드 (왼쪽 서브트리)
리프 노드: 3, 6, 4
최소 값: 3
- A의 두 번째 자식 노드 (오른쪽 서브트리)
리프 노드: 2, 7, 3, 5
최소 값: 2
따라서, A 노드에서 선택되는 값은
4. B 노드의 자식 노드들:
- B의 첫 번째 자식 노드 (왼쪽 서브트리)
리프 노드: 9, 3
최소 값: 3
- B의 두 번째 자식 노드 (가운데 서브트리)
리프 노드: 1, 2, 5
최소 값: 1
- B의 세 번째 자식 노드 (오른쪽 서브트리)
리프 노드: 7, 10, 4
최소 값: 4
따라서, B 노드에서 선택되는 값은
1. 루트 노드 (최대화 노드)에서 시작하여 A 노드를 탐색한다.
2. A 노드에서 첫 번째 자식 (최소화 노드) 탐색:
리프 노드: 3, 6, 4 중 최소 값: 3
3. A 노드에서 두 번째 자식 (최소화 노드) 탐색:
리프 노드: 2, 7, 3, 5 중 최소 값: 2
4. A 노드의 최소 값은 2이다. 현재
B 노드 탐색:
5. B 노드에서 첫 번째 자식 (최소화 노드) 탐색:
리프 노드: 9, 3 중 최소 값: 3 (3이 2보다 크므로 가지치기 적용 불가)
6. B 노드에서 두 번째 자식 (최소화 노드) 탐색:
리프 노드: 1, 2, 5 중 최소 값: 1
B 노드의 최소 값이 1이므로
이후의 탐색 (세 번째 자식 노드) 불필요로 가지치기 적용.
결과 선택
루트 노드의 최대 값은
결론:
3. 몬테카를로 트리 탐색의 선택, 확장, 시뮬레이션, 역전파라는 네 단계를 설명하라.
1) 선택(Selection): 루트 노드에서 시작하여 선택 전략에 따라 자식 노드를 선택하는 과정을 반복한다. 이 선택 과정은 아직 시도해보지 않은 행동이 남아 있는 노드에 도달할 때까지 반복한다.
2) 확장(Expansion): 선택된 노드에 새로운 행동을 하여 자식 노드를 생성해 트리에 추가하여 트리를 확장한다.
3) 시뮬레이션(Simulation): 확장된 노드로부터 시작하여 게임이 끝날 때까지 스스로 게임을 진행한다. 이 모의 게임의 결과는 게임에 따라 정해진 점수일 수도 있고, 승리(+1), 무승부(0), 패배(-1)라는 값이 사용될 수도 있다.
4) 역전파(Backpropagation): 시뮬레이션 결과를 확장된 노드로부터 루트 노드까지 선택 경로를 따라 역전파하여 통계를 업데이트한다.
1. 다음 최대최소 탐색트리에서 A의 평가함수와 다음으로 선택할 수는 무엇인가?
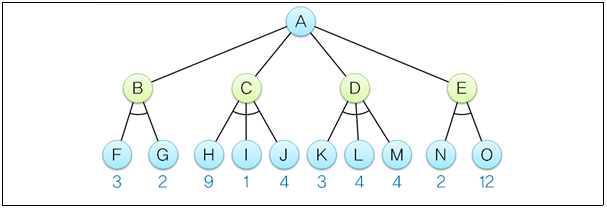
1) 3, B
2) 1, C
3) 3, D
4) 12, E
정답: 3
해설: 최소화 노드인 B, C, D, E의 평가함수는 후계노드의 평가함수들 중 가장 작은 값이므로 각각 2, 1, 3, 2이다. 최대화 노드인 A에서는 후계노드 중 평가함수 값이 가장 큰 것을 선택하므로 D를 다음 수로 선택한다.
2. α-β 가지치기에 대한 설명으로 올바른 것은?
1) 루트로부터 현재 노드까지의 경로비용에 따라 다음 노드를 선택한다.
2) 몬테카를로 트리 탐색을 위한 확장 전략이다.
3) 최소화 노드에서 한 후계노드의 가치가 v일 때 β>v라면 그 최소화 노드의 나머지 후계노드들은 가지치기한다.
4) 최대화 노드에서 한 후계노드의 가치가 v일 때 β≤v라면 그 최대화 노드의 나머지 후계노드들은 가지치기한다.
정답: 4
해설: α-β 가지치기는 최대최소 탐색트리에서 불필요한 가지를 잘라냄으로써 탐색의 성능을 높이기 위한 알고리즘이다. 최소화 노드에서 한 후계노드의 가치가 v일 때 α≥v라면 그 최소화 노드의 나머지 후계노드들은 가지치기한다. 또한 최대화 노드에서 한 후계노드의 가치가 v일 때 β≤v라면 그 최대화 노드의 나머지 후계노드들은 가지치기한다.
3. 다음 최대최소 탐색트리에서 α-β 가지치기를 적용할 경우 C의 나머지 후계노드들을 가지치기할 수 있는 x의 값에 해당되는 것은?
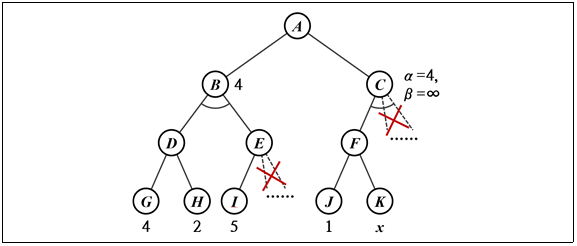
1) 2
2) 5
3) 8
4) 10
정답: 1
해설: K의 가치가 답항 ①~④의 값 중 하나일 경우 모두 J의 가치인 1보다 크므로 F의 가치 v는 x가 될 것이다. F는 최소화 노드인 C의 후계노드로서 현재의 α가 4이므로 α≥v(즉, 4≥x)인 경우 C의 나머지 후계노드들은 더 이상 검토해 볼 필요가 없다.
4. 다음 중 몬테카를로 트리 탐색에 대한 설명으로 올바른 것은?
1) 어떠한 상태의 가치를 추정할 수 있는 경험적 평가함수가 필요하다.
2) 롤아웃을 통해 탐색 과정에서 새로 생성된 노드의 가치를 추정한다.
3) 확장은 시뮬레이션 결과를 조상노드에 전달하여 통계를 업데이트하는 것이다.
4) 선택을 위한 전략은 탐사(exploration)는 고려하지 않고 활용(exploitation)에 중점을 둔다.
정답: 2
해설: 몬테카를로 트리 탐색에서 어떠한 상태에 대한 가치를 추정할 때 경험적 지식을 반영한 평가함수를 사용하는 방식이 아니라 탐색공간을 무작위 방식으로 스스로 게임을 끝까지 진행해 보는 몬테카를로 롤아웃을 하는 시뮬레이션에 의해 노드의 가치를 추정한다. 선택 전략은 탐사와 활용이 균형을 이룰 수 있도록 설계하며, 확장된 노드에서 시뮬레이션을 수행함으로써 계산된 가치는 역전파를 통해 루트 방향으로 조상노드를 따라 전달되어 조상노드들의 통계치를 업데이트한다.
참고 자료:
- 인공지능 (이광형,이병래 공저 | 한국방송통신대학교출판문화원 | 2018)



