비교 기반의 정렬이 아닌 데이터 기반의 정렬 방식으로 계수 정렬과 기수 정렬이 있다.
데이터 기반의 정렬은 입력 데이터에 대한 메타 정보가 주어지는 정렬로, 비교 기반 정렬의 하한인 O(nlogn)보다 좋은 성능 O(n)을 낼 수 있는 정렬이다. 단, 데이터 분포에 대한 정보가 주어져야 한다.
예를 들어, 아래와 같은 데이터 입력이 주어진다고 할 때, 데이터의 분포는 4 ~ 9이다.
int[] arr = {7, 5, 9, 8, 4, 5, 7, 5};
이 글에서는 데이터 기반 정렬 중 하나인 계수 정렬에 대해 살펴본다.
계수 정렬
아이디어
아이디어는 2가지 부분으로 나뉜다.
1) 입력 값에서 데이터가 발생한 횟수를 구한다.
2) 발생한 횟수를 기반으로 누적 횟수를 구한다.
작동 원리
이 배열을 갖고 작동 원리를 살펴보자.
{7, 5, 9, 8, 4, 5, 7, 5}
이 배열을 살펴 보면 데이터 발생 횟수는 4 ~9 까지의 범위 중
{1, 3, 0, 2, 1, 1}이 될 것이다. 이때 인덱스는 다음과 같이 매핑된다.
0 -> 4
1 -> 5
2 -> 6
3 -> 7
4 -> 8
5 -> 9
즉, 데이터의 범위의 min 값이 4이며, max 값이 9라는 정보를 바탕으로 카운팅 배열을 형성한 것이다.
해당 배열을 다시 탐색하여 이제는 누적 배열을 구한다. 누적 배열을 구하면 다음과 같다.
{1, 4, 4, 6, 7, 8}
이 배열의 의미는 각 인덱스에 해당하는 배열이 어느 위치에 등장하는가를 표현해주는 것이다. 즉, 인덱스 0 = 4라는 요소는 몇 번째에 위치할 것인가를 알려준다.
누적 값의 의미를 생각해보면 된다. 5라는 데이터는 그 앞에 4개가 존재하기 때문에 마지막에 위치하는 최대 인덱스가 4가 될 것을 의미하는 것이다.
여기까지의 과정을 실제 코드 작동으로 살펴보자.
그렇다면 이렇게 누적한 배열을 갖고 어떻게 정렬을 한다는 것일까?
다시 생각을 해보면, 정렬해야 하는 데이터는 현재 다음과 같다.
{7, 5, 9, 8, 4, 5, 7, 5}
이 데이터를 끝에서부터 탐색해보자. 맨 처음 요소인 5부터 처리한다.
5가 의미하는 것이 무엇일까? 누적배열이 {1, 4, 4, 6, 7, 8}인 상황에서 5는 2번째 인덱스를 의미하며, 4라는 값을 나타내고 있다. 이 4라는 값은 데이터가 정렬이 되었을 때 요소 5의 맨 마지막 위치가 4임을 뜻하는 것이다.
따라서 카운팅 정렬이 진행되는 반복문 수행에서 첫 번째 반복이 지나면
정렬 배열은 다음과 같이 구성된다.
{_ _ _ 5 _ _ _ _}
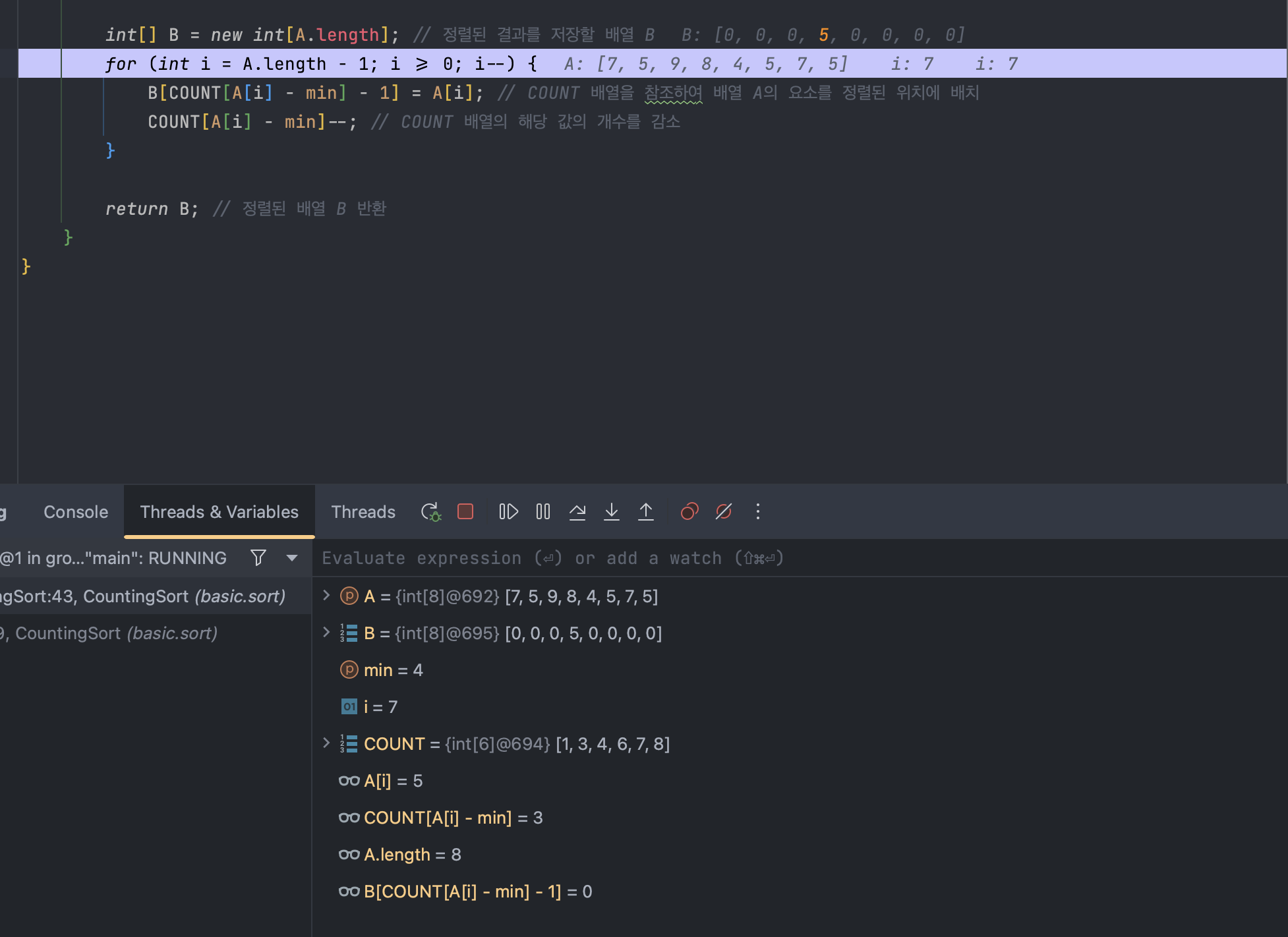
이렇게 요소를 배치하고 나면 카운트 배열에서 4라는 값을 하나 쓴 것이 되므로 해당 요소를 하나 줄여준다.
따라서 카운팅 배열은 {1, 3, 4, 6, 7, 8}이 된다.
이 부분, 정렬 배열을 초기화하는 부분이 조금 복잡해 보일 수 있는데
B[COUNT[A[i] - min] - 1] = A[i]; // COUNT 배열을 참조하여 배열 A의 요소를 정렬된 위치에 배치즉, 카운트 배열 의 보정된 인덱스 (4 -> 0을 찾아야 하므로) -min을 해주고 그렇게 하여 찾은 카운트 배열의 위치가 곧 정렬 배열의 인덱스가 되므로 해당 인덱스에 요소를 넣어준다는 것이다.
다음으로 계속해서 반복문이 진행되며 이제 다음 요소인 7에 대해서 탐색하고 배치한다.
마찬가지의 로직을 수행하므로 이제 정렬 배열은 다음과 같이 구성된다.
{_ _ _ 5 _ 7 _ _}

이 과정을 반복하여
최종적으로 {4, 5, 5, 7, 7, 8 ,9}라는 정렬 결과를 얻게 된다
그렇다면 성능은 어떻게 될까?
시간 복잡도
i) 최저값과 최고값을 탐색하는 부분 (현재 예시에서는 입력으로 주어짐) => O(n)
int MIN = A[0]; // 배열 A의 최솟값을 저장하는 변수
int MAX = A[0]; // 배열 A의 최댓값을 저장하는 변수
for (int i = 1; i < n; i++) {
if (A[i] < MIN) {
MIN = A[i];
}
if (A[i] > MAX) {
MAX = A[i];
}
ii) 카운트 배열을 초기화하고 누적 배열로 구성하는 부분 => O(k)
for (int j = 0; j < A.length; j++) {
COUNT[A[j] - min]++; // COUNT 배열의 인덱스는 A[j]의 값에서 최솟값을 뺀 값으로 해당 값의 개수를 카운트
}
for (int j = 1; j < COUNT.length; j++) {
COUNT[j] = COUNT[j] + COUNT[j - 1]; // COUNT 배열을 누적 개수로 업데이트
}
iii) 누적 배열을 바탕으로 정렬 배열을 구성하는 부분 => O(k)
for (int i = A.length - 1; i >= 0; i--) {
B[COUNT[A[i] - min] - 1] = A[i]; // COUNT 배열을 참조하여 배열 A의 요소를 정렬된 위치에 배치
COUNT[A[i] - min]--; // COUNT 배열의 해당 값의 개수를 감소
}
이때 입력 값의 범위 k가 입력 크기 n에 비례한다면 O(n + n)으로 나타낼 수 있으므로 최종 시간 복잡도는 O(n)으로 표기할 수 있게 된다.
특징
따라서 다음과 같은 특징으로 정리할 수 있다.
1. 입력값의 범위가 입력 원소의 개수보다 작거나 비례할 때 유용 => 그래야 O(n +k)인 선형 시간 성능을 갖게 된다.
2. 안정적인 알고리즘 o
3. 제자리 정렬 알고리즘 x
4. 입력값의 범위라는 사전 정보를 필요로 하므로 보편적인 방식이라고는 할 수 없다.
자바 구현 코드
import java.util.Arrays;
public class CountingSort {
public static void main(String[] args) {
// int[] arr1 = {4, 2, 1, 7, 3};
// int[] sortedArr1 = countingSort(arr1, 8, 1); // 입력값 범위: 1부터 8
// System.out.println("원본 배열: " + Arrays.toString(arr1) + " 정렬된 배열: " + Arrays.toString(sortedArr1));
//
// int[] arr2 = {9, 5, 1, 3, 7};
// int[] sortedArr2 = countingSort(arr2, 10, 1); // 입력값 범위: 1부터 10
// System.out.println("원본 배열: " + Arrays.toString(arr2) + " 정렬된 배열: " + Arrays.toString(sortedArr2));
//
// int[] arr3 = {8, 4, 2, 6, 10};
// int[] sortedArr3 = countingSort(arr3, 10, 2); // 입력값 범위: 2부터 10
// System.out.println("원본 배열: " + Arrays.toString(arr3) + " 정렬된 배열: " + Arrays.toString(sortedArr3));
int[] arr4 = {7, 5, 9, 8, 4, 5, 7, 5};
int[] sortedArr4 = countingSort(arr4, 9, 4); // 입력값 범위: 4부터 9
System.out.println("원본 배열: " + Arrays.toString(arr4) + " 정렬된 배열: " + Arrays.toString(sortedArr4));
}
/**
* Counting Sort 알고리즘을 사용하여 배열 A를 정렬하는 메서드입니다.
*
* @param A 정렬할 배열
* @param max 배열 A의 최댓값 (입력값의 범위)
* @param min 배열 A의 최솟값 (입력값의 범위)
* @return 정렬된 배열 B
*/
public static int[] countingSort(int[] A, int max, int min) {
int[] COUNT = new int[max - min + 1]; // COUNT 배열의 크기는 최댓값과 최솟값의 차이에 1을 더한 값
for (int j = 0; j < A.length; j++) {
COUNT[A[j] - min]++; // COUNT 배열의 인덱스는 A[j]의 값에서 최솟값을 뺀 값으로 해당 값의 개수를 카운트
}
for (int j = 1; j < COUNT.length; j++) {
COUNT[j] = COUNT[j] + COUNT[j - 1]; // COUNT 배열을 누적 개수로 업데이트
}
int[] B = new int[A.length]; // 정렬된 결과를 저장할 배열 B
for (int i = A.length - 1; i >= 0; i--) {
B[COUNT[A[i] - min] - 1] = A[i]; // COUNT 배열을 참조하여 배열 A의 요소를 정렬된 위치에 배치
COUNT[A[i] - min]--; // COUNT 배열의 해당 값의 개수를 감소
}
return B; // 정렬된 배열 B 반환
}
}
'알고리즘 > 기초' 카테고리의 다른 글
| 자바 숫자의 자릿수를 판별하는 5가지 방식 (1) | 2023.06.21 |
|---|---|
| 자바 문자열 역순 뒤집기 4가지 방법 (1) | 2023.06.21 |
| 절대값을 이용한 i, j의 증감 규칙 찾기 (절대값과 나머지를 이용하기) (0) | 2023.06.18 |
| 퀵 정렬 (Quick Sort) - 아이디어, 작동 원리, 성능 및 시간 복잡도, 특징, 자바 구현 코드 (0) | 2023.06.11 |
| 선택 정렬, 아이디어, 작동 원리, 자바 구현 코드 (0) | 2023.06.10 |

