[프로그래머스] 당구 연습 (거울계 좌표를 이용하기, 자바 풀이)

https://school.programmers.co.kr/learn/courses/30/lessons/169198

📌 문제

프로그래머스의 마스코트인 머쓱이는 최근 취미로 당구를 치기 시작했습니다.

머쓱이는 손 대신 날개를 사용해야 해서 당구를 잘 못 칩니다. 하지만 끈기가 강한 머쓱이는 열심히 노력해서 당구를 잘 치려고 당구 학원에 다니고 있습니다.

오늘도 당구 학원에 나온 머쓱이에게 당구 선생님이"원쿠션"(당구에서 공을 쳐서 벽에 맞히는 걸 쿠션이라고 부르고, 벽에 한 번 맞힌 후 공에 맞히면 원쿠션이라고 부릅니다) 연습을 하라면서 당구공의 위치가 담긴 리스트를 건네줬습니다. 리스트에는 머쓱이가 맞춰야 하는 공들의 위치가 담겨있습니다. 머쓱이는 리스트에 담긴 각 위치에 순서대로 공을 놓아가며 "원쿠션" 연습을 하면 됩니다. 이때, 머쓱이는 항상 같은 위치에 공을 놓고 쳐서 리스트에 담긴 위치에 놓인 공을 맞춥니다.

머쓱이와 달리 최근 취미로 알고리즘 문제를 풀기 시작한 당신은, 머쓱이가 친 공이 각각의 목표로한 공에 맞을 때까지 최소 얼마의 거리를 굴러가야 하는지가 궁금해졌습니다.

당구대의 가로 길이 m, 세로 길이 n과 머쓱이가 쳐야 하는 공이 놓인 위치 좌표를 나타내는 두 정수 startX, startY, 그리고 매 회마다 목표로 해야하는 공들의 위치 좌표를 나타내는 정수 쌍들이 들어있는 2차원 정수배열 balls가 주어집니다. "원쿠션" 연습을 위해 머쓱이가 공을 적어도 벽에 한 번은 맞춘 후 목표 공에 맞힌다고 할 때, 각 회마다 머쓱이가 친 공이 굴러간 거리의 최솟값의 제곱을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.

단, 머쓱이가 친 공이 벽에 부딪힐 때 진행 방향은 항상 입사각과 반사각이 동일하며, 만약 꼭짓점에 부딪힐 경우 진입 방향의 반대방향으로 공이 진행됩니다. 공의 크기는 무시하며, 두 공의 좌표가 정확히 일치하는 경우에만 두 공이 서로 맞았다고 판단합니다. 공이 목표 공에 맞기 전에 멈추는 경우는 없으며, 목표 공에 맞으면 바로 멈춘다고 가정합니다.

⚔ 제한 사항

3 ≤ m, n ≤ 1,000
0 < startX < m
0 < startY < n
2 ≤ balls의 길이 ≤ 1,000
balls의 원소는 [a, b] 형태입니다.
- a, b는 머쓱이가 맞춰야 할 공이 놓인 좌표를 의미합니다.
- 0 < a < m, 0 < b < n
- (a, b) = ( startX, startY )인 입력은 들어오지 않습니다.

입출력 예

m	n	startX	startY	balls	result
10	10	3	7	[[7, 7], [2, 7], [7, 3]]	[52, 37, 116]

👀 문제 해석

이 문제는 당구대에서 공을 쳐서 반드시 벽을 한 번만 맞힌 뒤 목표 공을 맞추는 상황을 생각해, 각 목표 공에 대해 친 공이 이동하는 최소 거리의 제곱을 구하는 문제이다.

핵심 조건을 명확히 정리하면 다음과 같다.

당구대는 가로 길이 m, 세로 길이 n으로 주어진 직사각형이다.
출발점(친 공의 위치)은 고정된 좌표 (startX, startY)이다.
목표 공의 좌표들은 배열 balls에 주어진다. 각 목표 공마다 독립적으로 최소 이동 거리 제곱을 구해야 한다.
반드시 벽을 한 번 이상 맞춘 후 목표 공에 도달해야 한다.
- 직접 목표 공에 맞추는 직선 경로는 불가능하다.
벽에 닿을 때 입사각과 반사각이 같아야 하며, 모서리에 정확히 맞으면 반대 방향으로 반사된다.

이 조건들 중 특히 눈여겨 봐야 할 것은 바로 "벽을 꼭 한 번만 맞춘다"는 점이다.

단순하게 생각하면 공의 모든 이동 경로를 탐색해 최단 거리를 찾는 방식(BFS/DFS)도 떠올릴 수 있다. 그러나 여기서 단서가 등장한다.

당구공은 반사될 때 항상 입사각 = 반사각을 따른다. 이 원리를 바탕으로 거울을 생각해보면, 이 문제는 사실상 기하학적 문제로 바뀐다.

🔎 접근

문제를 처음 접했을 때 가장 먼저 든 생각은 "완전 탐색"이다. 당구공이 벽에 한 번 튕기고 목표 공까지 가는 모든 가능한 경로를 탐색하는 것이다. 당구대를 격자로 보고, 벽에 튕길 때마다 탐색 깊이가 하나씩 늘어나는 '거울 칸 격자' 모델을 상상해 보자. 여기서 '깊이'는 반사 횟수가 될 것이다. 이렇게 해서 최소 거리의 제곱을 찾을 수 있지 않을까?

하지만 문제의 핵심 조건 "벽을 꼭 한 번만 맞춘다" 와 "입사각=반사각" 이라는 단서에 따라 좀 더 단순하게 볼 수 있지 않을까?

당구공의 반사는 빛의 반사와 같다. 이 원리를 이용하면, 벽에 공이 튀는 것은 마치 벽 너머 '거울 좌표계'에 있는 반사된 목표 공을 향해 직선으로 공을 치는 것과 동일한 상황으로 치환할 수 있다. 즉, 경로 탐색 문제를 기하학으로 접근할 수 있는 것이다.

이렇게 되면 완전 탐색이 필요 없어지는데, 그 이유는 하나의 시작점과 여러 개의 목표지점이 존재하며, 문제의 요구사항은 정답이 반드시 존재하는 제약 조건에서 최소 거리를 구하는 것이기 때문이다. 또한 원쿠션만 탐색하면 되기 때문에, 하나의 거울 좌표계의 특정 지점을 바라보면 되는 경우만 탐색하면 되는 문제가 된다. 만약 쿠션의 개수가 n개로 증가한다면 그때는 DFS/BFS로 탐색이 필요해질 수도 있다. 이부분은 이 글의 하단에서 다시 논해본다.

이 "반사의 원리"라는 아이디어를 구체화해보면 다음과 같다.

네 개의 벽(상, 하, 좌, 우) 각각에 대해 목표 공을 반사시키는 방식이 훨씬 효율적이다.
"원쿠션"이라는 제약 덕분에, 딱 네 번의 반사 케이스만 고려하면 되기 때문이다.
이때, '네 벽 반사 공식(4-mirror)'에서 시간 복잡도는 각 공별로 $O(1)$ 이 된다.

이때, 문제를 푸는 주요 컴포넌트로서 객체 지향 모델링은 다음과 같이 할 수 있다.

Point: 당구공의 위치 (x, y 좌표)를 나타내는 단순한 데이터 객체이다. 두 Point 간의 거리 제곱을 계산하는 메서드를 가질 수 있다.
Wall: 공이 반사될 수 있는 네 방향의 벽(LEFT, RIGHT, TOP, BOTTOM)을 명확히 구분하기 위한 열거형(enum)으로 정의한다.
BilliardTable: 당구대의 크기(가로 m, 세로 n) 정보를 저장한다. 또한, 주어진 Point (목표 공)를 특정 Wall에 대해 반사시킨 새로운 Point (유령 공)의 좌표를 계산하는 기능을 제공한다.
Shot: 출발점에서 특정 Wall을 거쳐 원래 Point (목표 공)에 도달하는 한 번의 시도(경로)를 나타낸다. 이 객체는 내부적으로 반사된 목표점의 위치를 BilliardTable을 통해 계산하고, 해당 경로가 유효한지(isValid(), 즉 벽에 닿기 전에 원래 목표 공을 먼저 치는지) 판단하며, 유효할 경우 출발점에서 반사된 목표점까지의 거리 제곱을 계산하는 책임을 진다.

여기서 Shot 이 핵심 요소인데, 각 Shot에서 가장 중요한 것은 두 가지이다.

첫째는 반사된 목표점까지의 거리 계산이다. 이는 출발점과 반사된 목표점 사이의 직선 거리이며, 피타고라스 정리에 따라 $(\Delta x)^2 + (\Delta y)^2$로 그 거리의 제곱을 구할 수 있다.

둘째는 경로의 유효성(isValid()) 판단이다. 아무리 반사된 지점까지의 거리가 짧더라도, 그 경로가 실제 벽에 닿기 전에 원래 목표 공을 먼저 지나친다면 "원쿠션" 규칙 위반이다. 이 "경로 막힘" 현상은 특정 조건, 즉 좌/우 벽 반사 시에는 출발점과 목표 공의 y좌표(높이)가 같고 목표 공이 그 사이에 있을 때, 상/하 벽 반사 시에는 x좌표(가로선)가 같고 목표 공이 그 사이에 있을 때만 발생한다. (자세한 증명은 뒤에서 다룸.)

최종적으로 각 목표 공에 대해, 이 네 가지 potential shots (벽 반사 경로)를 생성하고, 유효한 경로들 중에서만 최소 제곱 거리를 찾는 방식으로 풀이 로직을 확정할 수 있다.

이 접근법은 각 공에 대해 상수 시간 계산만 필요하므로, 전체 시간 복잡도는 $O(\text{balls.length})$, 공간 복잡도는 추가적인 큰 자료구조를 사용하지 않으므로 $O(1)$이 된다.

Q1: 반사의 원리가 정확히 무엇인가? 그리고 '거울 속 목표 지점'은 어떻게 계산하나?

"반사의 원리"는 빛이 거울에 반사될 때처럼, 공이 벽에 부딪히는 입사각과 반사각이 같다는 것이다.

이를 좌표계로 옮겨오면, 예를 들어 목표 공 T(tx, ty)를 왼쪽 벽(x=0, 즉 y축)에 대해 반사시킨 유령 공 T'의 좌표는 (-tx, ty)가 된다.

y좌표는 그대로 두고 x좌표의 부호만 바꾸는 것이다.

마찬가지로 오른쪽 벽(x=m)에 대해서는 T'(2m-tx, ty), 위쪽 벽(y=n)에 대해서는 T'(tx, 2n-ty), 아래쪽 벽(y=0)에 대해서는 T'(tx, -ty)로 계산할 수 있다.

이렇게 찾은 유령 공 T'까지의 직선 거리는 피타고라스 정리를 이용해 $\sqrt{(\Delta x)^2 + (\Delta y)^2}$로 구하고, 문제에서 요구하는 것은 이 거리의 제곱이므로 최종적으로 $(\Delta x)^2 + (\Delta y)^2$을 사용한다.

<svg viewBox="0 0 1200 800" xmlns="http://www.w3.org/2000/svg">
  <!-- 배경 -->
  <rect width="1200" height="800" fill="#f8f9fa"/>
  
  <!-- 제목 -->
  <text x="600" y="30" text-anchor="middle" font-size="24" font-weight="bold" fill="#2c3e50">당구 반사의 원리 - 거울 좌표계 변환</text>
  
  <!-- 왼쪽 벽 반사 예시 -->
  <g transform="translate(50, 80)">
    <text x="150" y="0" text-anchor="middle" font-size="18" font-weight="bold" fill="#34495e">왼쪽 벽 반사 (x=0)</text>
    
    <!-- 당구대 -->
    <rect x="50" y="40" width="200" height="150" fill="none" stroke="#2c3e50" stroke-width="3"/>
    
    <!-- 좌표축 -->
    <line x1="30" y1="40" x2="30" y2="200" stroke="#7f8c8d" stroke-width="1"/>
    <line x1="25" y1="195" x2="280" y2="195" stroke="#7f8c8d" stroke-width="1"/>
    <text x="20" y="35" font-size="12" fill="#7f8c8d">y</text>
    <text x="285" y="200" font-size="12" fill="#7f8c8d">x</text>
    <text x="45" y="210" font-size="12" fill="#7f8c8d">0</text>
    
    <!-- 출발점 S -->
    <circle cx="120" cy="120" r="5" fill="#e74c3c"/>
    <text x="130" y="115" font-size="14" font-weight="bold" fill="#e74c3c">S(sx, sy)</text>
    
    <!-- 목표 공 T -->
    <circle cx="180" cy="100" r="5" fill="#3498db"/>
    <text x="190" y="95" font-size="14" font-weight="bold" fill="#3498db">T(tx, ty)</text>
    
    <!-- 반사된 유령 공 T' -->
    <circle cx="20" cy="100" r="5" fill="#9b59b6" stroke="#9b59b6" stroke-width="2" fill-opacity="0.5"/>
    <text x="-35" y="95" font-size="14" font-weight="bold" fill="#9b59b6">T'(-tx, ty)</text>
    
    <!-- 벽에서의 반사점 -->
    <circle cx="50" cy="110" r="3" fill="#f39c12"/>
    <text x="10" y="125" font-size="12" fill="#f39c12">반사점</text>
    
    <!-- 경로 -->
    <line x1="120" y1="120" x2="50" y2="110" stroke="#e74c3c" stroke-width="2" stroke-dasharray="5,5"/>
    <line x1="50" y1="110" x2="180" y2="100" stroke="#e74c3c" stroke-width="2"/>
    
    <!-- 직선 경로 (가상) -->
    <line x1="120" y1="120" x2="20" y2="100" stroke="#9b59b6" stroke-width="2" opacity="0.7"/>
    
    <!-- 수식 -->
    <text x="75" y="230" font-size="14" fill="#2c3e50">T'(-tx, ty) = (-180, 100)</text>
    <text x="75" y="250" font-size="14" fill="#2c3e50">거리² = (sx-(-tx))² + (sy-ty)²</text>
  </g>
  
  <!-- 오른쪽 벽 반사 예시 -->
  <g transform="translate(350, 80)">
    <text x="150" y="0" text-anchor="middle" font-size="18" font-weight="bold" fill="#34495e">오른쪽 벽 반사 (x=m)</text>
    
    <!-- 당구대 -->
    <rect x="50" y="40" width="200" height="150" fill="none" stroke="#2c3e50" stroke-width="3"/>
    
    <!-- 좌표축 -->
    <line x1="30" y1="40" x2="30" y2="200" stroke="#7f8c8d" stroke-width="1"/>
    <line x1="25" y1="195" x2="320" y2="195" stroke="#7f8c8d" stroke-width="1"/>
    <text x="20" y="35" font-size="12" fill="#7f8c8d">y</text>
    <text x="325" y="200" font-size="12" fill="#7f8c8d">x</text>
    <text x="245" y="210" font-size="12" fill="#7f8c8d">m</text>
    
    <!-- 출발점 S -->
    <circle cx="120" cy="120" r="5" fill="#e74c3c"/>
    <text x="80" y="135" font-size="14" font-weight="bold" fill="#e74c3c">S(sx, sy)</text>
    
    <!-- 목표 공 T -->
    <circle cx="180" cy="100" r="5" fill="#3498db"/>
    <text x="190" y="95" font-size="14" font-weight="bold" fill="#3498db">T(tx, ty)</text>
    
    <!-- 반사된 유령 공 T' -->
    <circle cx="270" cy="100" r="5" fill="#9b59b6" stroke="#9b59b6" stroke-width="2" fill-opacity="0.5"/>
    <text x="280" y="95" font-size="14" font-weight="bold" fill="#9b59b6">T'(2m-tx, ty)</text>
    
    <!-- 벽에서의 반사점 -->
    <circle cx="250" cy="110" r="3" fill="#f39c12"/>
    <text x="255" y="125" font-size="12" fill="#f39c12">반사점</text>
    
    <!-- 경로 -->
    <line x1="120" y1="120" x2="250" y2="110" stroke="#e74c3c" stroke-width="2" stroke-dasharray="5,5"/>
    <line x1="250" y1="110" x2="180" y2="100" stroke="#e74c3c" stroke-width="2"/>
    
    <!-- 직선 경로 (가상) -->
    <line x1="120" y1="120" x2="270" y2="100" stroke="#9b59b6" stroke-width="2" opacity="0.7"/>
    
    <!-- 수식 -->
    <text x="75" y="230" font-size="14" fill="#2c3e50">T'(2m-tx, ty) = (2×250-180, 100)</text>
    <text x="75" y="250" font-size="14" fill="#2c3e50">= (320, 100)</text>
  </g>
  
  <!-- 위쪽 벽 반사 예시 -->
  <g transform="translate(650, 80)">
    <text x="150" y="0" text-anchor="middle" font-size="18" font-weight="bold" fill="#34495e">위쪽 벽 반사 (y=n)</text>
    
    <!-- 당구대 -->
    <rect x="50" y="40" width="200" height="150" fill="none" stroke="#2c3e50" stroke-width="3"/>
    
    <!-- 좌표축 -->
    <line x1="30" y1="40" x2="30" y2="230" stroke="#7f8c8d" stroke-width="1"/>
    <line x1="25" y1="195" x2="280" y2="195" stroke="#7f8c8d" stroke-width="1"/>
    <text x="20" y="35" font-size="12" fill="#7f8c8d">y</text>
    <text x="285" y="200" font-size="12" fill="#7f8c8d">x</text>
    <text x="40" y="50" font-size="12" fill="#7f8c8d">n</text>
    
    <!-- 출발점 S -->
    <circle cx="120" cy="120" r="5" fill="#e74c3c"/>
    <text x="80" y="135" font-size="14" font-weight="bold" fill="#e74c3c">S(sx, sy)</text>
    
    <!-- 목표 공 T -->
    <circle cx="180" cy="100" r="5" fill="#3498db"/>
    <text x="190" y="95" font-size="14" font-weight="bold" fill="#3498db">T(tx, ty)</text>
    
    <!-- 반사된 유령 공 T' -->
    <circle cx="180" cy="20" r="5" fill="#9b59b6" stroke="#9b59b6" stroke-width="2" fill-opacity="0.5"/>
    <text x="190" y="15" font-size="14" font-weight="bold" fill="#9b59b6">T'(tx, 2n-ty)</text>
    
    <!-- 벽에서의 반사점 -->
    <circle cx="150" cy="40" r="3" fill="#f39c12"/>
    <text x="155" y="35" font-size="12" fill="#f39c12">반사점</text>
    
    <!-- 경로 -->
    <line x1="120" y1="120" x2="150" y2="40" stroke="#e74c3c" stroke-width="2" stroke-dasharray="5,5"/>
    <line x1="150" y1="40" x2="180" y2="100" stroke="#e74c3c" stroke-width="2"/>
    
    <!-- 직선 경로 (가상) -->
    <line x1="120" y1="120" x2="180" y2="20" stroke="#9b59b6" stroke-width="2" opacity="0.7"/>
    
    <!-- 수식 -->
    <text x="75" y="230" font-size="14" fill="#2c3e50">T'(tx, 2n-ty) = (180, 2×150-100)</text>
    <text x="75" y="250" font-size="14" fill="#2c3e50">= (180, 200)</text>
  </g>
  
  <!-- 아래쪽 벽 반사 예시 -->
  <g transform="translate(950, 80)">
    <text x="150" y="0" text-anchor="middle" font-size="18" font-weight="bold" fill="#34495e">아래쪽 벽 반사 (y=0)</text>
    
    <!-- 당구대 -->
    <rect x="50" y="40" width="200" height="150" fill="none" stroke="#2c3e50" stroke-width="3"/>
    
    <!-- 좌표축 -->
    <line x1="30" y1="40" x2="30" y2="230" stroke="#7f8c8d" stroke-width="1"/>
    <line x1="25" y1="195" x2="280" y2="195" stroke="#7f8c8d" stroke-width="1"/>
    <text x="20" y="35" font-size="12" fill="#7f8c8d">y</text>
    <text x="285" y="200" font-size="12" fill="#7f8c8d">x</text>
    <text x="45" y="210" font-size="12" fill="#7f8c8d">0</text>
    
    <!-- 출발점 S -->
    <circle cx="120" cy="120" r="5" fill="#e74c3c"/>
    <text x="80" y="135" font-size="14" font-weight="bold" fill="#e74c3c">S(sx, sy)</text>
    
    <!-- 목표 공 T -->
    <circle cx="180" cy="100" r="5" fill="#3498db"/>
    <text x="190" y="90" font-size="14" font-weight="bold" fill="#3498db">T(tx, ty)</text>
    
    <!-- 반사된 유령 공 T' -->
    <circle cx="180" cy="220" r="5" fill="#9b59b6" stroke="#9b59b6" stroke-width="2" fill-opacity="0.5"/>
    <text x="190" y="235" font-size="14" font-weight="bold" fill="#9b59b6">T'(tx, -ty)</text>
    
    <!-- 벽에서의 반사점 -->
    <circle cx="150" cy="190" r="3" fill="#f39c12"/>
    <text x="155" y="205" font-size="12" fill="#f39c12">반사점</text>
    
    <!-- 경로 -->
    <line x1="120" y1="120" x2="150" y2="190" stroke="#e74c3c" stroke-width="2" stroke-dasharray="5,5"/>
    <line x1="150" y1="190" x2="180" y2="100" stroke="#e74c3c" stroke-width="2"/>
    
    <!-- 직선 경로 (가상) -->
    <line x1="120" y1="120" x2="180" y2="220" stroke="#9b59b6" stroke-width="2" opacity="0.7"/>
    
    <!-- 수식 -->
    <text x="75" y="270" font-size="14" fill="#2c3e50">T'(tx, -ty) = (180, -100)</text>
  </g>
  
  <!-- 핵심 원리 설명 -->
  <g transform="translate(50, 420)">
    <rect x="0" y="0" width="1100" height="340" fill="#ecf0f1" stroke="#bdc3c7" stroke-width="2" rx="10"/>
    <text x="550" y="30" text-anchor="middle" font-size="20" font-weight="bold" fill="#2c3e50">반사의 원리와 거리 계산</text>
    
    <!-- 원리 설명 -->
    <text x="30" y="60" font-size="16" font-weight="bold" fill="#34495e">핵심 아이디어:</text>
    <text x="30" y="85" font-size="14" fill="#2c3e50">• 벽 반사를 "거울 너머의 가상 목표점"으로 변환</text>
    <text x="30" y="105" font-size="14" fill="#2c3e50">• 복잡한 반사 경로 → 단순한 직선 거리 계산</text>
    <text x="30" y="125" font-size="14" fill="#2c3e50">• 입사각 = 반사각 원리를 좌표 변환으로 구현</text>
    
    <!-- 공식 -->
    <text x="30" y="160" font-size="16" font-weight="bold" fill="#34495e">반사 좌표 공식:</text>
    
    <g transform="translate(50, 180)">
      <rect x="0" y="0" width="250" height="120" fill="white" stroke="#3498db" stroke-width="2" rx="5"/>
      <text x="125" y="20" text-anchor="middle" font-size="14" font-weight="bold" fill="#3498db">왼쪽 벽 (x=0)</text>
      <text x="20" y="40" font-size="12" fill="#2c3e50">T(tx, ty) → T'(-tx, ty)</text>
      <text x="20" y="60" font-size="12" fill="#2c3e50">x좌표: 부호 반전</text>
      <text x="20" y="80" font-size="12" fill="#2c3e50">y좌표: 유지</text>
      <text x="20" y="100" font-size="12" fill="#e74c3c">예: (180,100) → (-180,100)</text>
    </g>
    
    <g transform="translate(320, 180)">
      <rect x="0" y="0" width="250" height="120" fill="white" stroke="#e74c3c" stroke-width="2" rx="5"/>
      <text x="125" y="20" text-anchor="middle" font-size="14" font-weight="bold" fill="#e74c3c">오른쪽 벽 (x=m)</text>
      <text x="20" y="40" font-size="12" fill="#2c3e50">T(tx, ty) → T'(2m-tx, ty)</text>
      <text x="20" y="60" font-size="12" fill="#2c3e50">x좌표: 2m-tx</text>
      <text x="20" y="80" font-size="12" fill="#2c3e50">y좌표: 유지</text>
      <text x="20" y="100" font-size="12" fill="#e74c3c">예: (180,100) → (320,100)</text>
    </g>
    
    <g transform="translate(590, 180)">
      <rect x="0" y="0" width="250" height="120" fill="white" stroke="#f39c12" stroke-width="2" rx="5"/>
      <text x="125" y="20" text-anchor="middle" font-size="14" font-weight="bold" fill="#f39c12">위쪽 벽 (y=n)</text>
      <text x="20" y="40" font-size="12" fill="#2c3e50">T(tx, ty) → T'(tx, 2n-ty)</text>
      <text x="20" y="60" font-size="12" fill="#2c3e50">x좌표: 유지</text>
      <text x="20" y="80" font-size="12" fill="#2c3e50">y좌표: 2n-ty</text>
      <text x="20" y="100" font-size="12" fill="#e74c3c">예: (180,100) → (180,200)</text>
    </g>
    
    <g transform="translate(860, 180)">
      <rect x="0" y="0" width="220" height="120" fill="white" stroke="#9b59b6" stroke-width="2" rx="5"/>
      <text x="110" y="20" text-anchor="middle" font-size="14" font-weight="bold" fill="#9b59b6">아래쪽 벽 (y=0)</text>
      <text x="20" y="40" font-size="12" fill="#2c3e50">T(tx, ty) → T'(tx, -ty)</text>
      <text x="20" y="60" font-size="12" fill="#2c3e50">x좌표: 유지</text>
      <text x="20" y="80" font-size="12" fill="#2c3e50">y좌표: 부호 반전</text>
      <text x="20" y="100" font-size="12" fill="#e74c3c">예: (180,100) → (180,-100)</text>
    </g>
    
    <!-- 거리 계산 -->
    <text x="400" y="325" text-anchor="middle" font-size="16" font-weight="bold" fill="#2c3e50">
      최종 거리² = (sx - x')² + (sy - y')²  (여기서 (x', y')는 반사된 유령 공의 좌표)
    </text>
  </g>
  
  <!-- 범례 -->
  <g transform="translate(50, 770)">
    <circle cx="10" cy="0" r="5" fill="#e74c3c"/>
    <text x="20" y="5" font-size="12" fill="#2c3e50">출발점 S</text>
    
    <circle cx="100" cy="0" r="5" fill="#3498db"/>
    <text x="110" y="5" font-size="12" fill="#2c3e50">목표 공 T</text>
    
    <circle cx="200" cy="0" r="5" fill="#9b59b6" fill-opacity="0.5" stroke="#9b59b6" stroke-width="2"/>
    <text x="210" y="5" font-size="12" fill="#2c3e50">반사된 유령 공 T'</text>
    
    <line x1="350" y1="0" x2="380" y2="0" stroke="#e74c3c" stroke-width="2"/>
    <text x="390" y="5" font-size="12" fill="#2c3e50">실제 경로</text>
    
    <line x1="480" y1="0" x2="510" y2="0" stroke="#9b59b6" stroke-width="2" opacity="0.7"/>
    <text x="520" y="5" font-size="12" fill="#2c3e50">직선 경로 (가상)</text>
  </g>
</svg>

문제의 주요 조건 중 하나는 경로 중간에 목표 공이 있으면 안된다는 것이다. 이 것은 어떻게 판단할까?

A: 이 중요한 조건, 즉 "벽에 도달하기 전에 목표 공을 먼저 치면 안 된다"는 것을 판단하기 위해 Shot 객체 내에 isValid() 메서드를 두자. 핵심은 다음과 같다.

1. 최적 경로 상의 방해물 확인:

우리가 '유령 공'(반사된 목표 공 T')을 향해 내 공(S)을 직선으로 친다고 가정했을 때, 이 직선 경로는 실제로는 벽의 특정 지점(W)에 맞고 꺾여 실제 목표 공(T)으로 향하게 된다. isValid()는 내 공(S)이 벽의 지점(W)에 도달하기 전에 그

S-W 직선 구간 위에 원래 목표 공(T)이 놓여 있는지를 확인해야 한다.

여기서 핵심은 목표 공(T)이 이 특정 S-W 경로를 정확히 가로막는 경우는 매우 특별한 기하학적 조건에서만 발생한다는 점이다.

2. 가로 막는 경우 판단:

좌/우 벽 반사의 경우: 내 공(S)과 목표 공(T)의 y좌표(높이)가 서로 같고, 동시에 목표 공(T)이 내 공(S)과 해당 벽 사이에 위치할 때이다.

예를 들어 왼쪽 벽 반사 시, S와 T의 y좌표가 같고, T의 x좌표가 S의 x좌표보다 작으면서 0보다 클 때 이 "경로 막힘"이 발생한다. 만약 y좌표가 다르다면, 목표 공 T는 S에서 유령 공 T'로 향하는 (따라서 S에서 W로 향하는) 그 정확한 직선 경로에서 살짝 벗어나 있게 되어 경로를 직접 막지 않는다.

상/하 벽 반사의 경우: 유사하게, 내 공(S)과 목표 공(T)의 x좌표(가로선)가 서로 같고, 목표 공(T)이 내 공(S)과 해당 벽 사이에 위치할 때 경로 막힘이 발생한다.

3. 왜 그럴까? - 수학적 증명:

이 조건이 성립하는 이유를 왼쪽 벽(x=0) 반사의 경우를 예로 들어 수학적으로 살펴보자.

출발점을 S(sx, sy), 실제 목표 공을 T(tx, ty), 그리고 T를 왼쪽 벽에 대해 반사시킨 '유령 공'을 T'(-tx, ty)라고 하자.
우리가 고려하는 최적 경로는 S에서 T'를 향해 직선으로 쏜 것이며, 이 직선이 왼쪽 벽(x=0)과 만나는 지점을 W라고 하자. 실제 공은 S에서 W까지만 직선으로 가고 W에서 튕겨 T로 향한다.
경로가 유효하지 않으려면, T가 선분 SW 위에 있어야 한다. 즉, S, T, W가 일직선상에 놓여야 하고, T가 S와 W 사이에 있어야 한다.
W는 S-T' 직선 위에 있으므로, S, T, W가 일직선이라는 것은 결국 S, T, T'가 모두 일직선상에 있어야 함을 의미한다.
세 점 S(sx, sy), T(tx, ty), T'(-tx, ty)가 일직선상에 있으려면, S와 T 사이의 기울기와 T와 T' 사이의 기울기가 같아야 한다.
T와 T' 사이의 기울기: $(ty - ty) / (-tx - tx) = 0 / (-2tx) = 0$ (단, $tx \neq 0$이어야 하며, 문제 조건상 공은 벽 위에 있지 않으므로 $tx > 0$).
즉, T와 T'를 잇는 선은 수평선이다.
따라서 S, T, T'가 일직선이 되려면 S와 T를 잇는 선 또한 수평선이어야 한다. 이는 S의 y좌표와 T의 y좌표가 같아야 함을 의미한다: sy = ty.
만약 sy ≠ ty 라면, S, T, T'는 일직선상에 있을 수 없으므로, T는 선분 SW 위에 정확히 놓일 수 없다.
sy = ty 인 경우, S, T, T'는 모두 같은 수평선 $y=sy$ 위에 놓인다. 이때 T가 S와 왼쪽 벽 W(0, sy) 사이에 있으려면 T의 x좌표 tx는 0과 sx 사이에 있어야 한다 ($0 < tx < sx$).
따라서, 왼쪽 벽 반사 경로가 유효하지 않으려면 (즉, T가 S-W 경로를 막으려면) sy = ty 이고 동시에 $0 < tx < sx$ 여야 한다. $0 < tx$는 문제의 입력 조건에서 보장되므로, 핵심 조건은 sy == ty && tx < sx 가 된다. Q.E.D.

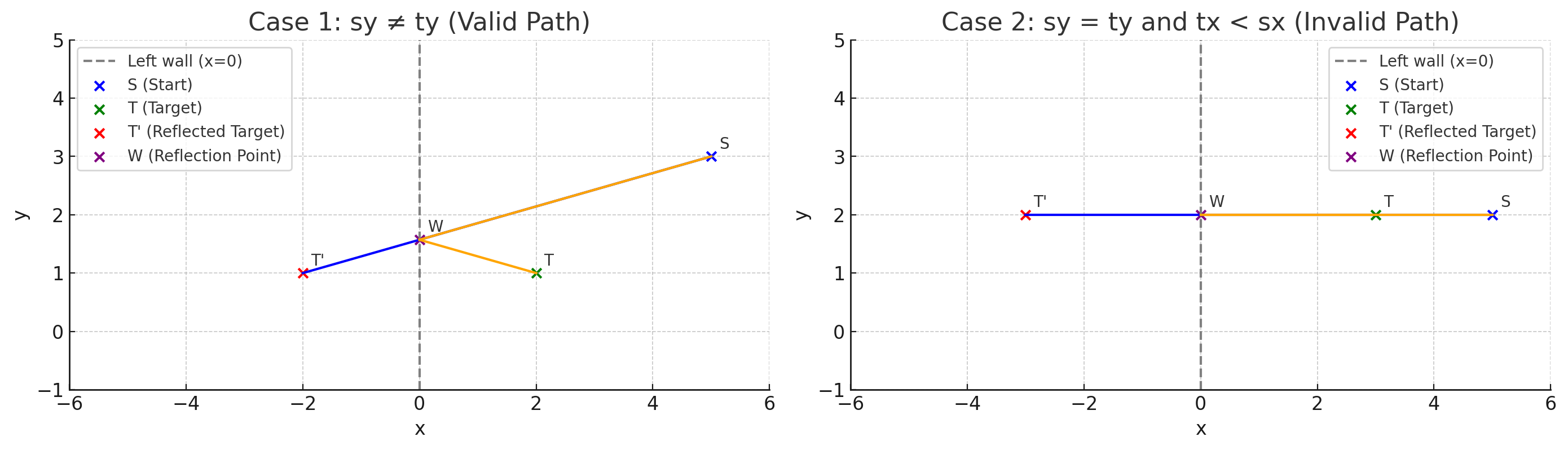
다른 벽(오른쪽, 위, 아래)의 경우도 동일한 원리로, 각각 x좌표 또는 y좌표가 일치하는 조건이 유도된다.
이에 따라, isValid() 메서드에서 해당 좌표 일치 조건을 사용할 수 있다.

💡 풀이 코드

이제 앞서 정리한 접근 방식과 객체 모델링을 바탕으로 실제 코드를 살펴보자. 문제에 주어진 예시 입력을 사용하여 따라가 본다.

예시 입력:

당구대 크기: m = 10, n = 10
내 공(S) 위치: startX = 3, startY = 7
목표 공(T)들: balls = [[7, 7], [2, 7], [7, 3]]

📜 코드 준비 및 초기화

가장 먼저, solution 메서드가 호출되면 필요한 객체들을 초기화한다.

public int[] solution(int m, int n, int startX, int startY, int[][] balls) {
    // 1. 당구대 객체 생성
    BilliardTable table = new BilliardTable(m, n);
    //    현실: table.width = 10, table.height = 10

    // 2. 내 공(출발점) Point 객체 생성
    Point startPoint = new Point(startX, startY);
    //    현실: startPoint.x = 3, startPoint.y = 7

    List<Integer> answerList = new ArrayList<>(); // 각 목표 공까지의 최소 거리 제곱을 저장할 리스트

    // ... 루프 시작 ...
}

BilliardTable 객체는 당구대의 가로(m), 세로(n) 크기 정보를 갖는다. 이 정보는 나중에 목표 공을 벽에 반사시킬 때 사용된다.
startPoint는 내 공의 고정된 시작 위치를 나타낸다.

🔄 각 목표 공에 대한 처리 루프

balls 배열에 담긴 각 목표 공에 대해 최소 거리 제곱을 계산하는 루프가 실행된다. 첫 번째 목표 공 T1 = [7, 7]을 예로 들어보자.

   // for (int[] ballCoords : balls) 루프 내부
   // 현재 ballCoords = [7, 7]

   Point targetPoint = new Point(ballCoords[0], ballCoords[1]);
   //    현실: targetPoint.x = 7, targetPoint.y = 7 (이것이 T1)

   int minSquaredDistance = Integer.MAX_VALUE; // 최소값을 찾기 위해 매우 큰 값으로 초기화

✨ Potential Shots (유령 공) 생성 및 계산

이제 startPoint에서 targetPoint (T1)를 각 네 방향 벽에 한 번 튕겨 맞추는 경우, 즉 4개의 "Potential Shots"를 고려한다.

각 Shot 객체가 생성될 때, 내부적으로 BilliardTable.reflectTarget() 메서드가 호출되어 '유령 공'의 위치(reflectedTargetPosition)가 계산된다.

   // 네 방향 벽에 대한 Shot 객체 생성
   Shot[] potentialShots = {
      new Shot(startPoint, targetPoint, Wall.LEFT, table),   // Shot 1
      new Shot(startPoint, targetPoint, Wall.RIGHT, table),  // Shot 2
      new Shot(startPoint, targetPoint, Wall.TOP, table),    // Shot 3
      new Shot(startPoint, targetPoint, Wall.BOTTOM, table) // Shot 4
   };

Shot 1: 왼쪽 벽(Wall.LEFT) 반사 (S=(3,7), T1=(7,7), table=(10,10))

Shot 생성자 내부:
- reflectedTargetPosition = table.reflectTarget(T1, Wall.LEFT) 호출
- BilliardTable.reflectTarget 내부: new Point(-T1.x, T1.y) => new Point(-7, 7)
- reflectedTargetPosition (유령 공 T1')은 (-7, 7)이 된다.

Shot 2: 오른쪽 벽(Wall.RIGHT) 반사

Shot 생성자 내부:
- reflectedTargetPosition = table.reflectTarget(T1, Wall.RIGHT) 호출
- BilliardTable.reflectTarget 내부: new Point(2 * table.width - T1.x, T1.y) => new Point(2 * 10 - 7, 7) => new Point(13, 7)
- reflectedTargetPosition (유령 공 T1'')은 (13, 7)이 된다.

Shot 3: 위쪽 벽(Wall.TOP) 반사

Shot 생성자 내부:
- reflectedTargetPosition = table.reflectTarget(T1, Wall.TOP) 호출
- BilliardTable.reflectTarget 내부: new Point(T1.x, 2 * table.height - T1.y) => new Point(7, 2 * 10 - 7) => new Point(7, 13)
- reflectedTargetPosition (유령 공 T1''')은 (7, 13)이 된다.

Shot 4: 아래쪽 벽(Wall.BOTTOM) 반사

Shot 생성자 내부:
- reflectedTargetPosition = table.reflectTarget(T1, Wall.BOTTOM) 호출
- BilliardTable.reflectTarget 내부: new Point(T1.x, -T1.y) => new Point(7, -7)
- reflectedTargetPosition (유령 공 T1'''')은 (7, -7)이 된다.

이제 4개의 Shot 객체가 각각의 반사된 목표점(유령 공) 정보를 가지게 되었다.

당구 테이블 벽면 반사 시뮬레이션

S (3,7) - 시작점

T1 (7,7) - 목표점

유령 공 - 반사된 목표점

LEFT

RIGHT

TOP

BOTTOM

(3,7)

(7,7)

T1'

(-7,7)

T1''

(13,7)

T1'''

(7,13)

T1''''

(7,-7)

벽면 반사 계산 결과

Shot 1 - LEFT 벽 반사:
new Point(-T1.x, T1.y) = (-7, 7)

Shot 2 - RIGHT 벽 반사:
new Point(2×width-T1.x, T1.y) = (2×10-7, 7) = (13, 7)

Shot 3 - TOP 벽 반사:
new Point(T1.x, 2×height-T1.y) = (7, 2×10-7) = (7, 13)

Shot 4 - BOTTOM 벽 반사:
new Point(T1.x, -T1.y) = (7, -7)

✅ 유효성 검사 및 최소 거리 제곱 업데이트

생성된 각 Shot에 대해 isValid()를 호출하여 경로가 유효한지 검사하고, 유효하다면 getSquaredDistance()를 호출하여 거리의 제곱을 계산한 후 minSquaredDistance를 업데이트한다.

T1 = (7,7) 에 대한 각 Shot 처리:
startPoint S = (3,7), originalTargetPosition T1 = (7,7)

Shot 1 (왼쪽 벽 반사, 유령 공 T1'(-7,7)):
- shot.isValid():
  - reflectionWall은 LEFT.
  - startPoint.y (7) == originalTargetPosition.y (7): 참.
  - originalTargetPosition.x (7) < startPoint.x (3): 거짓.
  - (참 && 거짓)은 거짓.
  - !거짓은 참(true). 경로 유효.
- shot.getSquaredDistance(): startPoint.squaredDistanceTo(T1'(-7,7))
  - dx = 3 - (-7) = 10
  - dy = 7 - 7 = 0
  - 10*10 + 0*0 = 100.
- minSquaredDistance = Math.min(Integer.MAX_VALUE, 100) = 100.
Shot 2 (오른쪽 벽 반사, 유령 공 T1''(13,7)):
- shot.isValid():
  - reflectionWall은 RIGHT.
  - startPoint.y (7) == originalTargetPosition.y (7): 참.
  - originalTargetPosition.x (7) > startPoint.x (3): 참.
  - (참 && 참)은 참.
  - !참은 거짓(false). 경로 무효. (내 공이 오른쪽 벽으로 가기 전에 (7,7)의 목표 공을 먼저 지나침)
- 이 Shot은 무시된다.
Shot 3 (위쪽 벽 반사, 유령 공 T1'''(7,13)):
- shot.isValid():
  - reflectionWall은 TOP.
  - startPoint.x (3) == originalTargetPosition.x (7): 거짓.
  - !(거짓 && ...)은 !거짓이므로 참(true). 경로 유효.
- shot.getSquaredDistance(): startPoint.squaredDistanceTo(T1'''(7,13))
  - dx = 3 - 7 = -4
  - dy = 7 - 13 = -6
  - (-4)*(-4) + (-6)*(-6) = 16 + 36 = 52.
- minSquaredDistance = Math.min(100, 52) = 52.
Shot 4 (아래쪽 벽 반사, 유령 공 T1''''(7,-7)):
- shot.isValid():
  - reflectionWall은 BOTTOM.
  - startPoint.x (3) == originalTargetPosition.x (7): 거짓.
  - !(거짓 && ...)은 !거짓이므로 참(true). 경로 유효.
- shot.getSquaredDistance(): startPoint.squaredDistanceTo(T1'''' (7,-7))
  - dx = 3 - 7 = -4
  - dy = 7 - (-7) = 14
  - (-4)*(-4) + 14*14 = 16 + 196 = 212.
- minSquaredDistance = Math.min(52, 212) = 52.

루프가 끝나면, 첫 번째 목표 공 [7,7]에 대한 minSquaredDistance는 52가 된다. 이 값이 answerList에 추가된다.

Shot 유효성 검사 및 최소 거리 계산

범례: 🔴 S(3,7) 시작점 | 🔵 T1(7,7) 목표점 | ● 유효한 경로 | ● 무효한 경로

LEFT

RIGHT

TOP

BOTTOM

(3,7)

(7,7)

T1'

(-7,7)

T1''

(13,7)

T1'''

(7,13)

T1''''

(7,-7)

유효성 검사 결과

Shot 1 - LEFT 벽 반사 ✅
isValid(): 참 (직진 가능)

거리² = (3-(-7))² + (7-7)² = 10² + 0² = 100

Shot 2 - RIGHT 벽 반사 ❌
isValid(): 거짓 (목표공을 먼저 지나침)

계산 생략

Shot 3 - TOP 벽 반사 ✅
isValid(): 참 (서로 다른 x좌표)

거리² = (3-7)² + (7-13)² = (-4)² + (-6)² = 52

Shot 4 - BOTTOM 벽 반사 ✅
isValid(): 참 (서로 다른 x좌표)

거리² = (3-7)² + (7-(-7))² = (-4)² + 14² = 212

최소 거리² 계산:
min(100, 52, 212) = 52
→ T1에 대한 최단 경로는 TOP 벽 반사

이와 동일한 과정을 나머지 balls 배열의 목표 공들([2,7], [7,3])에 대해서도 반복한다.

두 번째 목표 공 T2 = [2,7]의 경우: minSquaredDistance는 37이 계산될 것이다.
- 주요 유효 경로는 위쪽 벽 반사 T2_T(2,13): (3-2)^2 + (7-13)^2 = 1^2 + (-6)^2 = 1+36=37.
- 왼쪽 벽 반사는 T2_L(-2,7)인데, startY(7)==targetY(7) 이고 targetX(2)<startX(3) 이므로 유효하지 않게 된다. (문제 예시에서 설명된 부분)
세 번째 목표 공 T3 = [7,3]의 경우: minSquaredDistance는 116이 계산될 것이다.
- 주요 유효 경로는 위쪽 벽 반사 T3_T(7,17): (3-7)^2 + (7-17)^2 = (-4)^2 + (-10)^2 = 16+100=116.

모든 목표 공에 대한 계산이 끝나면 answerList는 [52, 37, 116]이 되고, 이를 int[] 배열로 변환하여 반환한다.

   // ... 루프 종료 ...

   // List<Integer>를 int[]로 변환
   return answerList.stream().mapToInt(Integer::intValue).toArray();
}

각 목표 공에 대한 4 방향 반사를 고려하고, 유효 판단에 따라 최단 거리의 제곱을 찾아내면 된다.

🎯 성능 분석 및 평가

앞서 언급했듯이 이 방식의 시간 복잡도는 크지 않다. 또한 이 문제에서는 DFS/BFS 를 사용할 필요 없이 주어진 데이터에 대해서만 직관적으로 탐색하면 되었다.

다만, 성능의 구체적인 계산을 좀 더 알아보고, 만약 문제가 조금 바뀐다면 어떻게 대처할 수 있을지에 대해서 추가로 살펴보고자 한다.

먼저 시간 복잡도이다.

각 목표 공(ball)에 대해 정확히 4개의 Shot 객체를 생성한다. 각 Shot 객체를 생성할 때 반사점 계산, isValid() 메서드를 통한 유효성 검사, getSquaredDistance()를 통한 거리 제곱 계산은 모두 고정된 연산 횟수, 즉 $O(1)$ 시간 안에 완료된다.

따라서 balls 배열의 길이가 $N$이라고 할 때, 전체 시간 복잡도는 $O(N)$이 된다.

공간 복잡도 역시 결과를 저장하기 위한 answerList (최종적으로 $N$개의 원소를 가짐)를 제외하면, 각 목표 공을 처리하는 과정에서 생성되는 객체들(Point, BilliardTable, Shot 등)의 수는 상수 개이므로,추가적으로 사용하는 메모리는 $O(1)$이라고 볼 수 있다.

문제의 제약 조건이 원쿠션이 아니라 N 쿠션이라면 어떻게 달라질까 ?

현재의 '네 벽 반사 공식'은 "원쿠션"이라는 특수한 상황에 최적화되어 있다.

만약 문제가 "벽에 N번 반사 후 목표 공 맞추기"와 같이 일반화된다면 이 방식은 직접 적용하기 어렵다.

이런 경우에는 처음에 고려했던 BFS/DFS 방식을 다시 고려해보아야 한다.

상태 정의: (현재 공의 위치, 남은 반사 횟수) 등을 상태로 정의할 수 있다.
탐색: 현재 위치에서 각 네 벽으로 공을 반사시켜 '다음 거울 칸'으로 이동하는 것을 간선으로 보고 탐색을 진행한다. 목표 공(또는 N번 반사된 목표 공의 이미지)에 도달하면 경로를 찾은 것이다.
최단 경로: BFS를 사용하면 최소 반사 횟수 또는 최소 누적 거리(의 제곱)를 찾는 데 유리하다.
유효성 검사: N쿠션 문제에서도 "벽에 닿기 전에 (중간 또는 최종) 목표 공을 먼저 치는 경우"는 여전히 주의해야 할 조건이다. 각 반사 단계에서 이러한 경로를 적절히 필터링하거나, 목표 도달 조건에 반영해야 한다.

즉, 쿠션 조건이 일반화되면 그래프 탐색 기법이 필요하다.

🚀 최종 제출 코드

import java.util.ArrayList;
import java.util.List;
import java.util.Objects;

class Solution {

	public int[] solution(int m, int n, int startX, int startY, int[][] balls) {
		
	}

	public static class Point {
		final int x;
		final int y;

		Point(int x, int y) {
			this.x = x;
			this.y = y;
		}

		// 두 점 사이의 거리 제곱을 계산 (오버플로우 방지를 위해 long 사용 후 int로 변환)
		public int squaredDistanceTo(Point other) {
			long dx = (long)this.x - other.x;
			long dy = (long)this.y - other.y;
			return (int)(dx * dx + dy * dy);
		}

		@Override
		public boolean equals(Object o) {
			if (this == o) {
				return true;
			}
			if (o == null || getClass() != o.getClass()) {
				return false;
			}
			Point point = (Point)o;
			return x == point.x && y == point.y;
		}

		@Override
		public int hashCode() {
			return Objects.hash(x, y);
		}
	}

	enum Wall {
		LEFT, RIGHT, TOP, BOTTOM
	}

	public static class BilliardTable {
		final int width;
		final int height;

		BilliardTable(int m, int n) {
			this.width = m;
			this.height = n;
		}

		/**
		 * 특정 벽에 대해 목표 지점(target)을 반사시킨 가상의 목표 지점을 계산한다.
		 * <p>
		 * 공이 벽에 부딪혀 목표 지점으로 향하는 최단 경로는, 마치 벽이 거울인 것처럼
		 * 벽 너머에 있는 '반사된 목표 지점'을 향해 직선으로 나아가는 경로와 동일하다.
		 * 각 벽에 대한 반사점 계산 원리는 다음과 같다 (당구대의 좌하단이 (0,0)이라고 가정):
		 * </p>
		 * <ol>
		 * <li><b>왼쪽 벽 (x=0, 즉 Y축) 에 대한 반사</b>:
		 * <ul>
		 * <li>목표점의 Y좌표는 변하지 않는다.</li>
		 * <li>X좌표는 Y축을 기준으로 대칭 이동한다. 즉, 원래 X좌표가 {@code target.x}라면,
		 * Y축까지의 거리는 {@code target.x}이고, 반사점의 X좌표는 Y축의 반대편으로
		 * 같은 거리만큼 이동하여 {@code -target.x}가 된다.</li>
		 * <li>따라서 반사된 지점은 {@code (-target.x, target.y)} 이다.</li>
		 * </ul>
		 * </li>
		 * <li><b>오른쪽 벽 (x=width) 에 대한 반사</b>:
		 * <ul>
		 * <li>목표점의 Y좌표는 변하지 않는다.</li>
		 * <li>X좌표는 {@code x=width} 직선을 기준으로 대칭 이동한다.</li>
		 * <li>원래 X좌표 {@code target.x}에서 오른쪽 벽까지의 거리는 {@code width - target.x} 이다.</li>
		 * <li>반사점의 X좌표는 오른쪽 벽 너머로 이 거리만큼 더 간 위치이므로,
		 * {@code width + (width - target.x) = 2 * width - target.x}가 된다.</li>
		 * <li>따라서 반사된 지점은 {@code (2 * width - target.x, target.y)} 이다.</li>
		 * </ul>
		 * </li>
		 * <li><b>위쪽 벽 (y=height) 에 대한 반사</b>:
		 * <ul>
		 * <li>목표점의 X좌표는 변하지 않는다.</li>
		 * <li>Y좌표는 {@code y=height} 직선을 기준으로 대칭 이동합니다.</li>
		 * <li>원래 Y좌표 {@code target.y}에서 위쪽 벽까지의 거리는 {@code height - target.y} 입니다.</li>
		 * <li>반사점의 Y좌표는 위쪽 벽 너머로 이 거리만큼 더 간 위치이므로,
		 * {@code height + (height - target.y) = 2 * height - target.y}가 됩니다.</li>
		 * <li>따라서 반사된 지점은 {@code (target.x, 2 * height - target.y)} 입니다.</li>
		 * </ul>
		 * </li>
		 * <li><b>아래쪽 벽 (y=0, 즉 X축) 에 대한 반사</b>:
		 * <ul>
		 * <li>목표점의 X좌표는 변하지 않는다.</li>
		 * <li>Y좌표는 X축을 기준으로 대칭 이동한다. 즉, 원래 Y좌표가 {@code target.y}라면,
		 * X축까지의 거리는 {@code target.y}이고, 반사점의 Y좌표는 X축의 반대편으로
		 * 같은 거리만큼 이동하여 {@code -target.y}가 된다.</li>
		 * <li>따라서 반사된 지점은 {@code (target.x, -target.y)} 이다.</li>
		 * </ul>
		 * </li>
		 * </ol>
		 *
		 * @param target 반사시킬 원래 목표 지점의 {@link Point} 객체
		 * @param wall   반사가 일어나는 벽의 종류 ({@link Wall} 열거형)
		 * @return 벽에 대해 반사된 새로운 가상의 목표 지점의 {@link Point} 객체
		 * @throws IllegalArgumentException 알 수 없는 {@link Wall} 타입이 입력된 경우 (Enum 사용 시 정상적으로는 발생하지 않음)
		 */
		public Point reflectTarget(Point target, Wall wall) {
			switch (wall) {
				case LEFT:
					return new Point(-target.x, target.y);
				case RIGHT:
					return new Point(2 * width - target.x, target.y);
				case TOP:
					return new Point(target.x, 2 * height - target.y);
				case BOTTOM:
					return new Point(target.x, -target.y);
				default:
					throw new IllegalArgumentException("Unknown wall type");
			}
		}
	}

	// 단일 시도(경로)를 나타내는 객체
	static class Shot {
		private final Point startPosition;
		private final Point originalTargetPosition;
		private final Point reflectedTargetPosition;
		private final Wall reflectionWall;

		Shot(Point startPosition, Point originalTargetPosition, Wall reflectionWall, BilliardTable table) {
			this.startPosition = startPosition;
			this.originalTargetPosition = originalTargetPosition;
			this.reflectionWall = reflectionWall;
			this.reflectedTargetPosition = table.reflectTarget(originalTargetPosition, reflectionWall);
		}


		/**
		 * 이 경조가 유효한지 (벽에 도달하기 전에 목표 공을 먼저 치는지) 판단
		 * <p>
		 * "원쿠션" 규칙은 공이 벽에 먼저 맞고 목표 공을 맞춰야 함을 의미한다.
		 * 이 함수는 반사의 원리로 계산된 특정 최적 경로가 규칙을 위반하는지 확인한다,
		 * <ol>
		 * <li>반사된 '유령 목표 공'을 향해 직선으로 칠 때, 그 경로가 벽에 닿기 전에
		 * 실제 목표 공의 위치를 먼저 지나면 해당 경로는 유효하지 않다.</li>
		 * <li>이러한 "경로 막힘" 현상은 다음 특정 조건에서만 발생한다.
		 * <ul>
		 * <li>좌/우 벽 반사 시: 출발점과 목표 공의 y좌표(높이)가 같고,
		 * 목표 공이 출발점과 해당 벽 사이에 위치할 때.</li>
		 * <li>상/하 벽 반사 시: 출발점과 목표 공의 x좌표(가로선)가 같고,
		 * 목표 공이 출발점과 해당 벽 사이에 위치할 때.</li>
		 * </ul>
		 * <li><b>수학적 증명 (좌측 벽 반사 예시)</b>:
		 *     <ul>
		 *         <li>출발점 S(sx, sy), 목표 공 T(tx, ty), T를 좌측 벽(x=0)에 반사한 유령 공 T'(-tx, ty).</li>
		 *         <li>공이 벽에 맞는 지점 W는 S와 T'를 잇는 직선이 x=0과 만나는 점이다.</li>
		 *         <li>T가 S와 W 사이에 있어 경로를 막으려면 S, T, W가 일직선상에 있어야 한다.</li>
		 *         <li>W가 S-T' 직선 위의 점이므로, 결국 S, T, T'가 일직선상에 있어야 한다.</li>
		 *         <li>T와 T'의 y좌표는 ty로 같다. 따라서 T와 T'를 잇는 선은 수평선 (기울기 0).</li>
		 *         <li>따라서, S, T, T'가 일직선이려면 S와 T를 잇는 선도 수평선이어야 하므로, sy = ty 여야 한다. Q.E.D </li>
		 *         <li>다른 벽의 경우도 동일하게 증명됨. </li>
		 *         <li>즉, y좌표가 다르면 T는 S에서 T'로 향하는 (벽에 최적으로 반사되는) 직선 경로의 첫 번째 구간(S-W) 위에 정확히 놓일 수 없으므로, 아래와 같은 valid 함수가 구현됨. </li>
		 *     </ul>
		 * </li>
		 * <li>다른 모든 경우는 목표 공이 해당 최적 직선 경로를 막지 않으므로 유효</li>
		 * </ol>
		 * @return 경로가 유효하면 true, 그렇지 않으면 false.
		 */
		public boolean isValid() {
			switch (reflectionWall) {
				case LEFT: // 왼쪽 벽(x=0) 반사
					// 출발점과 목표점이 같은 y선상에 있고, 목표점이 출발점보다 왼쪽에 있으면 무효
					return !(startPosition.y == originalTargetPosition.y && originalTargetPosition.x < startPosition.x);
				case RIGHT: // 오른쪽 벽(x=m) 반사
					// 출발점과 목표점이 같은 y선상에 있고, 목표점이 출발점보다 오른쪽에 있으면 무효
					return !(startPosition.y == originalTargetPosition.y && originalTargetPosition.x > startPosition.x);
				case BOTTOM: // 아래쪽 벽(y=0) 반사
					// 출발점과 목표점이 같은 x선상에 있고, 목표점이 출발점보다 아래쪽에 있으면 무효
					return !(startPosition.x == originalTargetPosition.x && originalTargetPosition.y < startPosition.y);
				case TOP: // 위쪽 벽(y=n) 반사
					// 출발점과 목표점이 같은 x선상에 있고, 목표점이 출발점보다 위쪽에 있으면 무효
					return !(startPosition.x == originalTargetPosition.x && originalTargetPosition.y > startPosition.y);
				default:
					return false; 
			}
		}

		public int getSquaredDistance() {
			return startPosition.squaredDistanceTo(reflectedTargetPosition);
		}
	}



}

저작자표시 비영리 변경금지 (새창열림)

'알고리즘 > 프로그래머스' 카테고리의 다른 글

[프로그래머스] 타겟 넘버 (3가지 풀이 방식, DFS, 트리, 그리고 수학적 공식을 이용한 최적화) (0)	2025.05.24
[프로그래머스] 두개 뽑아서 더하기 (자바 & 코틀린 풀이) (0)	2025.05.21
[프로그래머스] 경주로 건설 (자바 풀이) (0)	2025.05.11
[프로그래머스] 네트워크 (자바 풀이) (0)	2025.04.29
[프로그래머스] 표 편집 (2021 카카오 채용연계형 인텁십, 자바 풀이) (0)	2024.09.30

르네의 영속성 컨텍스트

[프로그래머스] 당구 연습 (거울계 좌표를 이용하기, 자바 풀이)

📌 문제

⚔ 제한 사항

👀 문제 해석

🔎 접근

💡 풀이 코드

📜 코드 준비 및 초기화

🔄 각 목표 공에 대한 처리 루프

✨ Potential Shots (유령 공) 생성 및 계산

당구 테이블 벽면 반사 시뮬레이션

벽면 반사 계산 결과

✅ 유효성 검사 및 최소 거리 제곱 업데이트

Shot 유효성 검사 및 최소 거리 계산

유효성 검사 결과

🎯 성능 분석 및 평가

🚀 최종 제출 코드

'알고리즘 > 프로그래머스' 카테고리의 다른 글

티스토리툴바

[프로그래머스] 당구 연습 (거울계 좌표를 이용하기, 자바 풀이)

📌 문제

⚔ 제한 사항

👀 문제 해석

🔎 접근

💡 풀이 코드

📜 코드 준비 및 초기화

🔄 각 목표 공에 대한 처리 루프

✨ Potential Shots (유령 공) 생성 및 계산

당구 테이블 벽면 반사 시뮬레이션

벽면 반사 계산 결과

✅ 유효성 검사 및 최소 거리 제곱 업데이트

Shot 유효성 검사 및 최소 거리 계산

유효성 검사 결과

🎯 성능 분석 및 평가

🚀 최종 제출 코드

'알고리즘 > 프로그래머스' 카테고리의 다른 글

관련글

티스토리툴바