https://school.programmers.co.kr/learn/courses/30/lessons/67259
📌 문제
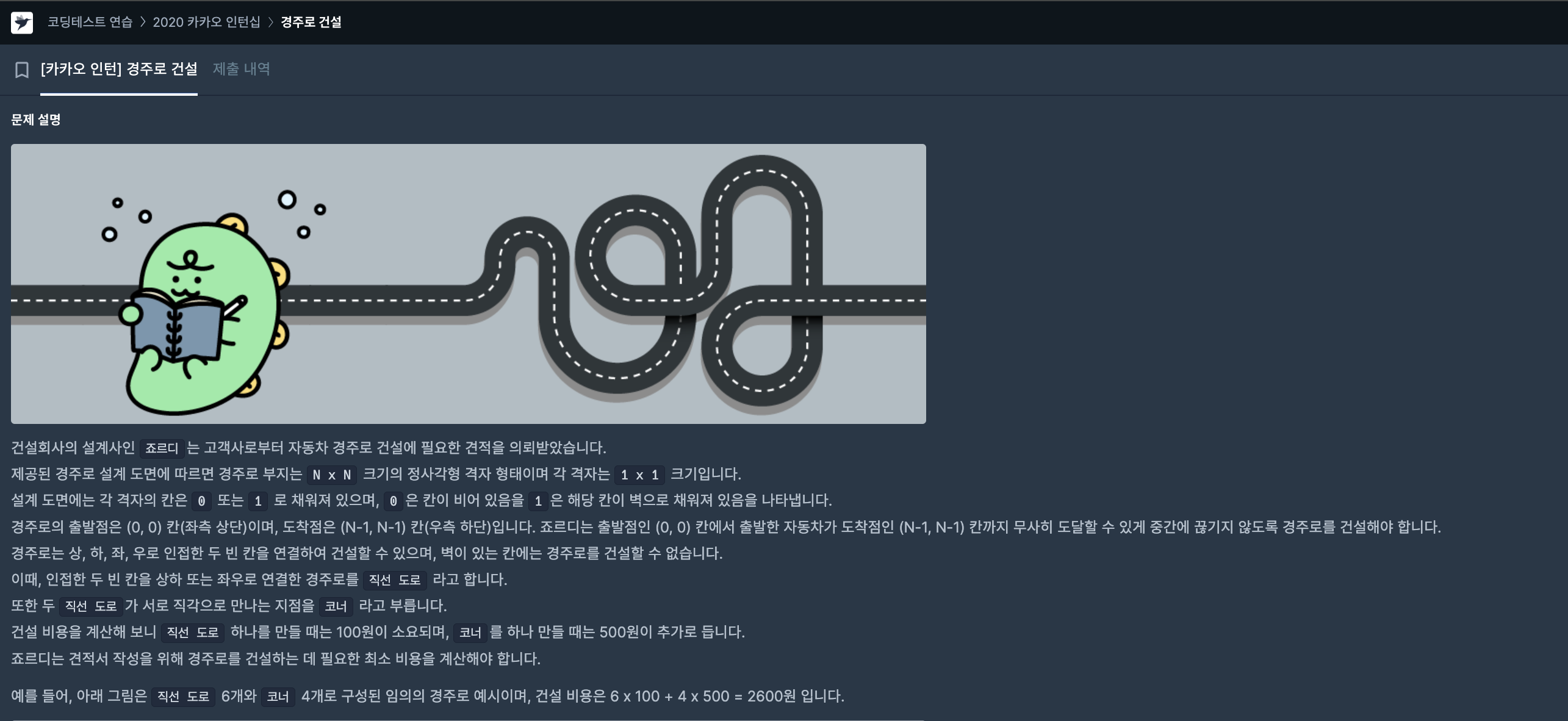
건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.
도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.
⚔ 제한 사항
[제한사항]
board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
board 배열의 각 원소의 값은 0 또는 1 입니다.
도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.
입출력 예
| [[0,0,0],[0,0,0],[0,0,0]] | 900 |
| [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] | 3800 |
| [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] | 2100 |
| [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] | 3200 |
👀 문제 해석
도면 위에 자동차 경주로를 깔아야 한다.
격자는 N × N 크기의 정사각형이고, 각 칸은 빈 칸(0) 또는 벽(1) 로 미리 정해져 있다. 출발점은 항상 (0, 0), 도착점은 (N − 1, N − 1)로 고정돼 있으며, 우리는 이 둘을 상·하·좌·우 네 방향 인접 칸만을 사용해 끊김 없이 연결해야 한다.
여기서 “연결”은 단순히 칸을 밟는 것이 아니라 도로를 시공하는 행위다. 같은 축으로 이어지는 구간은 직선 도로이며 한 칸마다 100원이 든다. 진행 방향이 달라져 직각이 되는 지점은 코너로 간주해 500원을 추가 낸다. 즉 직선 1칸 = 100원, 코너 1회 = 100 + 500 = 600원이 된다. 목표는 출발점에서 도착점까지 도로를 놓으면서 총 비용을 최소화하는 것이다.
문제를 뜯어 보면, 실제로 “가중치가 서로 다른 (100 또는 600) 그래프를 탐색해 최단비용 경로를 찾는 일”임을 알수 있다. 출발점과 도착점 모두 0이기 때문에 항상 적어도 한 경로는 존재한다는 전제가 깔려 있고, 문제에서는 가능한 모든 경로 중 건설 비용의 합이 가장 적은 경주로를 찾으면 된다. 다만, 보통의 BFS보다는 코너를 얼마나 감았는지에 따라 비용 누적을 추적할 수 있는 방식이 필요하며, 구현의 관점에서는 (행, 열)뿐 아니라 현재 진행 방향까지 상태로 저장해가며 탐색하는 꼴이 될 것이다.
따라서 이 문제는 최단 거리를 구하는 전형적인 탐색 문제와 유사하지만, 가중치가 “직선/코너”로 나뉘는 형태의 변형된 그래프 최단 비용 문제라고 볼 수 있다. 가중치가 두 가지뿐이므로 0-1 BFS나 다익스트라를 떠올릴 수 있다.
🔎 접근
"BFS 로 풀어야 하는 것은 알겠는데..."
이 문제를 처음 마주했을 때, 제 생각의 흐름은 다음과 같았다.
"BFS를 이용해야 한다는 것은 알겠는데, 길을 만들면서 실시간으로 거리 비용을 기록해주어야 할 것 같다. 그런데 비용은 직선과 코너별로 다르기 때문에, 직선이 무엇인지, 코너가 무엇인지를 알아야 한다. 해당 시점에서 직선인지 코너인지를 판별하려면 이전 길의 형태를 알아야 판단이 가능할 것 같은데..."
이 의문을 풀기 위해 생각을 조금 더 전개해보니, 실제로는 ‘같은 칸’을 방문하더라도 이전에 무슨 방향으로 왔는지에 따라 이후에 발생할 코너 비용이 달라진다는 점이 결정적이라는 결론에 이르게 되었다.
예를 들면 이런 식이다.
A → B → ?
↑ ↑
| |
다른 방향에서 온 두 경로가 같은 B칸에 위치
위 상황에서 A지점에서 B지점으로 이동했을 때,
- 위에서 온 경우(↑): B에서 오른쪽(→)으로 가면 코너가 생김 → 600원
- 왼쪽에서 온 경우(→): B에서 오른쪽(→)으로 가면 직선 유지 → 100원
즉, 위로 진행해오던 상태에서 같은 칸에 도달한 것과, 왼쪽으로 진행해오던 상태에서 도달한 것은 그다음 칸을 이동할 때 코너가 생기는지, 직선인지가 달라지는 것이다. 따라서 단순히 칸별 최소 비용만 저장하는 방식으로는 코너 비용을 제대로 반영할 수 없었고, "방향"을 함께 상태에 포함시키면 비용 정보 추적이 가능해진다.
<svg viewBox="0 0 600 400" xmlns="http://www.w3.org/2000/svg">
<!-- 격자 배경 -->
<defs>
<pattern id="grid" width="50" height="50" patternUnits="userSpaceOnUse">
<path d="M 50 0 L 0 0 0 50" fill="none" stroke="#ccc" stroke-width="1"/>
</pattern>
</defs>
<rect width="600" height="400" fill="url(#grid)" />
<!-- 첫 번째 경로: 아래에서 위로 올라온 후 오른쪽으로 (코너) -->
<g transform="translate(100, 200)">
<!-- 격자 강조 -->
<rect x="0" y="0" width="150" height="150" fill="none" stroke="#2C3E50" stroke-width="2" />
<!-- 경로 1: 아래에서 위로 올라온 다음 오른쪽으로 (코너) -->
<path d="M 75 150 L 75 75 L 150 75" stroke="#E74C3C" stroke-width="4" fill="none" />
<!-- 노드 A (시작) -->
<circle cx="75" cy="150" r="10" fill="#3498DB" />
<text x="75" y="150" dy="-15" text-anchor="middle" fill="#3498DB" font-weight="bold">A</text>
<!-- 노드 B (중간) -->
<circle cx="75" cy="75" r="10" fill="#2ECC71" />
<text x="75" y="75" dy="-15" text-anchor="middle" fill="#2ECC71" font-weight="bold">B</text>
<!-- 노드 C (끝) -->
<circle cx="150" cy="75" r="10" fill="#F39C12" />
<text x="150" y="75" dy="-15" text-anchor="middle" fill="#F39C12" font-weight="bold">C</text>
<!-- 방향 화살표 -->
<path d="M 75 120 L 75 90" stroke="#E74C3C" stroke-width="2" fill="none" marker-end="url(#arrow)" />
<path d="M 90 75 L 120 75" stroke="#E74C3C" stroke-width="2" fill="none" marker-end="url(#arrow)" />
<!-- 비용 -->
<text x="50" y="105" text-anchor="end" fill="#E74C3C" font-weight="bold">100원</text>
<text x="115" y="65" text-anchor="middle" fill="#E74C3C" font-weight="bold">600원</text>
<text x="75" y="30" text-anchor="middle" font-size="16" font-weight="bold">코너 발생 경로</text>
</g>
<!-- 두 번째 경로: 왼쪽에서 오른쪽으로 (직선) -->
<g transform="translate(350, 200)">
<!-- 격자 강조 -->
<rect x="0" y="0" width="150" height="150" fill="none" stroke="#2C3E50" stroke-width="2" />
<!-- 경로 2: 왼쪽에서 오른쪽으로 (직선) -->
<path d="M 0 75 L 75 75 L 150 75" stroke="#3498DB" stroke-width="4" fill="none" />
<!-- 노드 A (시작) -->
<circle cx="0" cy="75" r="10" fill="#3498DB" />
<text x="0" y="75" dy="-15" text-anchor="middle" fill="#3498DB" font-weight="bold">A</text>
<!-- 노드 B (중간) -->
<circle cx="75" cy="75" r="10" fill="#2ECC71" />
<text x="75" y="75" dy="-15" text-anchor="middle" fill="#2ECC71" font-weight="bold">B</text>
<!-- 노드 C (끝) -->
<circle cx="150" cy="75" r="10" fill="#F39C12" />
<text x="150" y="75" dy="-15" text-anchor="middle" fill="#F39C12" font-weight="bold">C</text>
<!-- 방향 화살표 -->
<path d="M 40 75 L 60 75" stroke="#3498DB" stroke-width="2" fill="none" marker-end="url(#arrow)" />
<path d="M 90 75 L 120 75" stroke="#3498DB" stroke-width="2" fill="none" marker-end="url(#arrow)" />
<!-- 비용 -->
<text x="40" y="65" text-anchor="middle" fill="#3498DB" font-weight="bold">100원</text>
<text x="115" y="65" text-anchor="middle" fill="#3498DB" font-weight="bold">100원</text>
<text x="75" y="30" text-anchor="middle" font-size="16" font-weight="bold">직선 유지 경로</text>
</g>
<!-- 상태값 설명 -->
<g transform="translate(50, 50)">
<text x="0" y="0" font-size="20" font-weight="bold">같은 B칸, 다른 방향 = 다른 상태</text>
<text x="0" y="30" font-size="16">⬆️ 위에서 도달한 B: 다음에 오른쪽으로 가면 코너 발생 (600원)</text>
<text x="0" y="55" font-size="16">➡️ 왼쪽에서 도달한 B: 다음에 오른쪽으로 가면 직선 유지 (100원)</text>
</g>
<!-- 화살표 마커 정의 -->
<defs>
<marker id="arrow" markerWidth="10" markerHeight="10" refX="9" refY="3" orient="auto" markerUnits="strokeWidth">
<path d="M0,0 L0,6 L9,3 z" fill="#000" />
</marker>
</defs>
</svg>
그렇다면 이제 실시간 cost를 추적할 방법을 알았으니 문제를 풀 수 있게 되었다.
그런데 이렇게 시뮬레이션이 포함된 문제에서는 상태와 행위가 꽤 명확하게 구분되기 때문에 객체 지향적으로 객체를 잘 모델링하면 은근 쉽게 문제가 풀린다. 따라서 다음과 같이 객체들을 먼저 모델링했다.
- 위치와 방향을 함께 표현하는 객체 - 같은 위치라도 어떤 방향으로 들어왔느냐에 따라 다른 상태로 취급
- 방향에 따른 비용 계산 로직 - 직선과 코너의 비용 차이를 명확히 표현할 수 있는 방식
- 탐색을 위한 상태 관리 객체 - 이미 방문한 위치와 방향의 조합에 대한 최소 비용을 기록
클래스로 구현하면,
- Node: 위치(row, col)와 방향(dir)을 함께 표현하는 클래스
- Dir: 방향을 표현하는 열거형 클래스로, 이동 및 비용 계산 로직을 포함
- Board: 게임판의 상태와 방문 기록(costs)을 관리하는 클래스
- Road: 현재까지의 경로와 누적 비용을 함께 표현하는 클래스
- Pose: 초기에 사용한 객체로 초기에는 위치 객체와 방향 객체를 구분하여 표현한 클래스 -> 향후 노드로 통합하여 사용
간단한 슈도코드로 살펴보면,
class Node {
int row, col
Dir dir // 이 칸에 어떤 방향으로 진입했는지
List<Node> next(Board board) {
// 현재 위치에서 상하좌우로 이동 가능한 노드 리스트 반환
}
int moveCostTo(Node nextNode) {
// 현재 노드에서 다음 노드로 이동 시 비용 계산 (직선/코너 구분)
return this.dir.moveCostTo(nextNode.dir)
}
}
enum Dir {
UP(-1, 0), DOWN(1, 0), LEFT(0, -1), RIGHT(0, 1)
int moveCostTo(Dir next) {
boolean sameAxis = (내 축과 next의 축이 같은지)
return sameAxis ? 100 : 600 // 직선이면 100, 코너면 600원
}
Node step(Node node) {
// 현재 노드에서 이 방향으로 한 칸 이동한 새 노드 반환
return new Node(node.row + deltaRow, node.col + deltaCol, this)
}
}
특히 핵심이 되는 로직은 Dir 열거형의 moveCostTo 메서드이다. 이 메서드로 인해 현재 방향과 다음 방향의 정보에 따라 직선인지 코너인지, 즉, 100 or 600 코스트를 반환한다.
int moveCostTo(Dir next) {
boolean sameAxis = isBothXAxis(next) || isBothYAxis(next);
return sameAxis ? 100 : 100 + 500; // 600원
}
private boolean isBothYAxis(Dir next) {
return this.deltaCol == 0 && next.deltaCol == 0; // 둘 다 세로축
}
private boolean isBothXAxis(Dir next) {
return this.deltaRow == 0 && next.deltaRow == 0; // 둘 다 가로축
}
또한 Board 클래스에서는 각 위치와 방향에 대한 최소 비용을 기록하기 위해 3차원 배열을 사용했다.
public class Board {
int[][] map; // 원본 지도 (0: 빈칸, 1: 벽)
int N; // 지도 크기
int[][][] costs; // [행][열][방향] = 최소비용
public boolean updateIfCheaper(Node node, int cost) {
int dirIndex = node.getDirIndex(); // 방향을 인덱스로 변환
if (cost < costs[node.row][node.col][dirIndex]) {
costs[node.row][node.col][dirIndex] = cost; // 더 저렴한 비용 기록
return true; // 비용이 갱신되었으므로 큐에 추가
}
return false; // 이미 더 저렴한 경로가 있음
}
public int minGoalCost() {
// 도착점에 도달한 모든 방향 중 최소 비용 반환
return Arrays.stream(costs[N-1][N-1]).min().orElse(Integer.MAX_VALUE);
}
}
그런데 왜 2차원이면 안될까?
2차원 배열은 칸마다 단 하나의 숫자만 저장한다. 만약 여기에 “가장 먼저 도착한 비용”을 기록해 버리면 다음과 같은 일이 생긴다.
- (0, 1) 칸에 오른쪽에서 100원으로 도착
- 배열에 100을 박아 둠
- 나중에 위에서 내려와 700원으로 같은 칸에 진입했을 때 현재 값 100보다 크니 무시 → 이 경로는 끊겨 버린다.
- 그런데 (0, 1) → (1, 1) → … 로 이어지는 더 싸고 짧은 전체 경로가 있었다면? 이미 지워졌으니 영영 발견하지 못한다.
즉 방향별로 갈라 보관하지 않으면 “지금은 좀 비싸더라도, 앞으로 코너를 덜 돌 수 있는 길”을 시도조차 못 하는 치명적인 탐색 손실이 생긴다.
그리고 이 최소 비용 배열 덕분에 기존의 visited 배열이 필요 없어진다.
visited 의 본래 목적은 두 가지다.
- 이미 본 상태를 다시 보지 않는다 – 무한 루프 방지
- 더 좋은(싼) 경로가 있을 때만 다시 본다 – 불필요한 연산 절감
3차원 costs 배열이 이 두 역할을 동시에 해 준다.
- 무한 루프: 한 방향 노드의 값은 오직 더 낮은 비용으로만 갱신된다. 양수 가중치 그래프에서 비용이 무한히 줄어드는 일은 없으므로 탐색은 자연히 끝난다.
- 연산 절감: updateIfCheaper() 가 “새 비용 < 기존 비용” 인 경우에만 true를 돌려 큐에 넣는다. 이미 더 싸게 방문한 상태는 큐에 다시 들어가지 않으니 중복 계산이 없다.
마지막으로, BFS 탐색을 위한 Road 클래스는 현재 탐색 중인 노드와 여기까지 오는 데 든 누적 비용을 함께 관리한다.
사실 전역 변수로 관리될 수 있는 누적 비용을 좀 Road가 들고 있는 것 뿐이다.
public static class Road {
Node node; // 현재 위치와 방향
int accumulatedCost; // 지금까지 누적된 비용
// 큐에 이 객체를 넣어 BFS 탐색
}
이렇게 객체 모델링이 끝나면 사실상 BFS 로직만 남은 상태가 된다.
얼핏 생각하면 실시간 누적 비용 계산이 복잡할 수 있지만, 이를 객체가 스스로 담당하는 메서드로 분리하고 나면 그렇게 어려운 일도 아니게 된다.
이제 풀이 코드을 살펴보고 작동 흐름을 한번 따라가보자.
💡 풀이 & 작동 분석
먼저 단계적으로 살펴보자.
1. 메인 솔루션 함수
public int solution(int[][] board) {
Board gameBoard = new Board(board);
return bfs(gameBoard);
}
메인 부분은 간단하다. 먼저 Board 객체를 초기화해준다. 사실 입력으로 주어진 2차원 배열 board를 써도 되지만, 앞서 언급했듯 나중에 쓰기 편하도록 객체로 관리해주는 것 뿐이다.
Board 객체는 다음과 같이 구성되어 있다.
public static class Board {
public int[][] map;
public int N;
public int[][][] costs; // [행][열][방향] = 비용 <- visited 까지 포함
public Board(int[][] arr) {
this.map = arr;
this.N = arr.length;
this.costs = new int[N][N][4];
Arrays.stream(costs).forEach(plane -> Arrays.stream(plane).forEach(line -> Arrays.fill(line, Integer.MAX_VALUE)));
}
public boolean updateIfCheaper(Node node, int cost) {
int dirIndex = node.getDirIndex();
if (cost < costs[node.row][node.col][dirIndex]) {
costs[node.row][node.col][dirIndex] = cost;
return true;
}
return false;
}
public int minGoalCost() {
return Arrays.stream(costs[N - 1][N - 1]).min().orElse(Integer.MAX_VALUE);
}
public boolean inRange(Node p) {
return 0 <= p.row && p.row < N && 0 <= p.col && p.col < N;
}
public boolean canMoveTo(Node p) {
return inRange(p) && map[p.row][p.col] == 0;
}
public boolean isGoal(Node p) {
return p.row == N - 1 && p.col == N - 1;
}
public void recordStartCost(Node startNode) {
updateIfCheaper(startNode, 0);
}
}
시뮬레이션에서 갈 수 있는 방향 탐색 메서드를 구현하고 있고, 비용도 관리한다. 이를 위한 비용 갱신 메서드 updateIfCheaper() 와 목표 도달 비용 계산하는 minGoalCost()도 갖고 있다.
초기화가 완료되었으면 이제 BFS로 탐색해주면 된다.
2. BFS 탐색 구현
public int bfs(Board board) {
Queue<Road> queue = new ArrayDeque<>();
Node startRight = new Node(0, 0, Dir.RIGHT);
Node startDown = new Node(0, 0, Dir.DOWN);
board.recordStartCost(startRight);
board.recordStartCost(startDown);
queue.add(new Road(startRight, 0));
queue.add(new Road(startDown, 0));
while (!queue.isEmpty()) {
Road currentRoad = queue.poll();
Node currentNode = currentRoad.node;
int currentCost = currentRoad.accumulatedCost;
if (board.isGoal(currentNode)) {
continue; // 다른 방향이 더 쌀 수도 있으니 계속 탐색
}
for (Node nextNode : currentNode.next(board)) {
int nextCost = currentCost + currentNode.moveCostTo(nextNode);
if (board.updateIfCheaper(nextNode, nextCost)) {
queue.add(new Road(nextNode, nextCost));
}
}
}
return board.minGoalCost();
}
시작점이 정해져 있으니 출발을 해주면 되는데, 두 방향으로 시작해주어야 한다는 점을 놓치기 쉽다. 따라서 이전 방향이 오른쪽인 케이스, 이전 방향이 아래쪽으로 향하던 케이스를 가정하여 넣어주어야 한다.
// 이부분
Node startRight = new Node(0, 0, Dir.RIGHT);
Node startDown = new Node(0, 0, Dir.DOWN);
무슨 말이냐면, 출발점 (0,0) 은 “방향” 이 정해지지 않은 특수한 칸이다.
만약 “오른쪽(R)만” 시작으로 넣고 탐색을 돌리면, 세 번째 테스트 케이스처럼 출발 직후 오른쪽이 벽(1)이라 막혀 있는 상황에서
0 0 1 0
0 0 0 0
0 1 0 1
1 0 0 0
1️⃣ 첫 큐가 `(0,0,R)` 하나뿐이라 바로 막다른 길에 부딪혀 비용이 무한대 →
2️⃣ “아래(D)로 내려가면 살 길이 있는데” 그 상태가 애초에 큐에 없으니
3️⃣ 도달 가능 경로 자체를 발견하지 못하고 탐색이 끝나 버린다.
따라서 출발점에서는 “R·D 두 방향을 동시에 큐에 넣어” 양쪽으로 뻗어 보게 만들어야 모든 케이스에서 최적 경로가 보장된다.
<svg viewBox="0 0 800 550" xmlns="http://www.w3.org/2000/svg">
<!-- 배경 그리드 -->
<defs>
<pattern id="smallGrid" width="25" height="25" patternUnits="userSpaceOnUse">
<path d="M 25 0 L 0 0 0 25" fill="none" stroke="#eee" stroke-width="0.5"/>
</pattern>
<pattern id="grid" width="100" height="100" patternUnits="userSpaceOnUse">
<rect width="100" height="100" fill="url(#smallGrid)"/>
<path d="M 100 0 L 0 0 0 100" fill="none" stroke="#ccc" stroke-width="1"/>
</pattern>
<marker id="arrowhead" markerWidth="10" markerHeight="7" refX="0" refY="3.5" orient="auto">
<polygon points="0 0, 10 3.5, 0 7" fill="#000"/>
</marker>
</defs>
<!-- 제목 -->
<text x="400" y="40" text-anchor="middle" font-size="24" font-weight="bold" fill="#333">시작점의 방향 고려가 필요한 이유</text>
<!-- 왼쪽 설명 -->
<g transform="translate(60, 90)">
<text x="0" y="0" font-size="18" font-weight="bold" fill="#333">1. 오른쪽 방향만 고려할 경우 문제점</text>
<text x="0" y="30" font-size="14" fill="#555">출발점에서 오른쪽 방향으로만 시작하면</text>
<text x="0" y="50" font-size="14" fill="#555">오른쪽이 벽인 경우 더 이상 진행할 수 없음</text>
<!-- 맵 그리기 -->
<g transform="translate(0, 70)">
<!-- 격자 배경 -->
<rect width="280" height="280" fill="#f8f9fa" stroke="#adb5bd" stroke-width="2" />
<!-- 가로 선 -->
<line x1="0" y1="70" x2="280" y2="70" stroke="#adb5bd" stroke-width="1" />
<line x1="0" y1="140" x2="280" y2="140" stroke="#adb5bd" stroke-width="1" />
<line x1="0" y1="210" x2="280" y2="210" stroke="#adb5bd" stroke-width="1" />
<!-- 세로 선 -->
<line x1="70" y1="0" x2="70" y2="280" stroke="#adb5bd" stroke-width="1" />
<line x1="140" y1="0" x2="140" y2="280" stroke="#adb5bd" stroke-width="1" />
<line x1="210" y1="0" x2="210" y2="280" stroke="#adb5bd" stroke-width="1" />
<!-- 시작점 -->
<rect x="5" y="5" width="60" height="60" fill="#4dabf7" opacity="0.6" rx="5" ry="5" />
<text x="35" y="40" font-size="16" text-anchor="middle" fill="#212529" font-weight="bold">0,0</text>
<!-- 벽 -->
<rect x="145" y="5" width="60" height="60" fill="#fa5252" opacity="0.8" rx="5" ry="5" />
<text x="175" y="40" font-size="16" text-anchor="middle" fill="#212529" font-weight="bold">벽</text>
<!-- 도착점 -->
<rect x="215" y="215" width="60" height="60" fill="#40c057" opacity="0.6" rx="5" ry="5" />
<text x="245" y="250" font-size="16" text-anchor="middle" fill="#212529" font-weight="bold">도착</text>
<!-- 방향 화살표 -->
<path d="M 65 35 L 140 35" stroke="#f03e3e" stroke-width="3" stroke-dasharray="5,5" marker-end="url(#arrowhead)" />
<text x="100" y="25" font-size="12" text-anchor="middle" fill="#f03e3e" font-weight="bold">불가능!</text>
<!-- 설명 텍스트 -->
<text x="140" y="310" text-anchor="middle" font-size="14" fill="#333" font-weight="bold">오른쪽만 고려 → 경로 없음</text>
</g>
</g>
<!-- 오른쪽 설명 -->
<g transform="translate(430, 90)">
<text x="0" y="0" font-size="18" font-weight="bold" fill="#333">2. 모든 가능한 시작 방향 고려</text>
<text x="0" y="30" font-size="14" fill="#555">출발점에서 오른쪽과 아래쪽 방향 모두 시작하면</text>
<text x="0" y="50" font-size="14" fill="#555">최적의 경로를 찾을 수 있음</text>
<!-- 맵 그리기 -->
<g transform="translate(0, 70)">
<!-- (0,0) -> (1,0) -> (2,0) -> ... -> (3,3) 경로 표시 -->
<!-- 격자 배경 -->
<rect width="280" height="280" fill="#f8f9fa" stroke="#adb5bd" stroke-width="2" />
<!-- 가로 선 -->
<line x1="0" y1="70" x2="280" y2="70" stroke="#adb5bd" stroke-width="1" />
<line x1="0" y1="140" x2="280" y2="140" stroke="#adb5bd" stroke-width="1" />
<line x1="0" y1="210" x2="280" y2="210" stroke="#adb5bd" stroke-width="1" />
<!-- 세로 선 -->
<line x1="70" y1="0" x2="70" y2="280" stroke="#adb5bd" stroke-width="1" />
<line x1="140" y1="0" x2="140" y2="280" stroke="#adb5bd" stroke-width="1" />
<line x1="210" y1="0" x2="210" y2="280" stroke="#adb5bd" stroke-width="1" />
<!-- 시작점 -->
<rect x="5" y="5" width="60" height="60" fill="#4dabf7" opacity="0.6" rx="5" ry="5" />
<text x="35" y="40" font-size="16" text-anchor="middle" fill="#212529" font-weight="bold">0,0</text>
<!-- 벽 -->
<rect x="145" y="5" width="60" height="60" fill="#fa5252" opacity="0.8" rx="5" ry="5" />
<rect x="145" y="145" width="60" height="60" fill="#fa5252" opacity="0.8" rx="5" ry="5" />
<rect x="215" y="145" width="60" height="60" fill="#fa5252" opacity="0.8" rx="5" ry="5" />
<!-- 도착점 -->
<rect x="215" y="215" width="60" height="60" fill="#40c057" opacity="0.6" rx="5" ry="5" />
<text x="245" y="250" font-size="16" text-anchor="middle" fill="#212529" font-weight="bold">도착</text>
<!-- 경로 -->
<path d="M 35 35 L 35 105 L 105 105 L 175 105 L 175 175 L 245 175 L 245 245"
stroke="#228be6" stroke-width="4" fill="none" marker-end="url(#arrowhead)" />
<!-- 방향 화살표 -->
<path d="M 35 65 L 35 105" stroke="#1971c2" stroke-width="3" marker-end="url(#arrowhead)" />
<text x="20" y="85" font-size="12" text-anchor="middle" fill="#1971c2" font-weight="bold">아래</text>
<!-- 설명 텍스트 -->
<text x="140" y="310" text-anchor="middle" font-size="14" fill="#333" font-weight="bold">아래쪽도 고려 → 경로 발견</text>
</g>
</g>
<!-- 코드 설명 섹션 -->
<g transform="translate(60, 450)">
<rect width="680" height="80" fill="#f1f3f5" stroke="#dee2e6" stroke-width="2" rx="5" ry="5" />
<text x="20" y="30" font-size="16" font-family="monospace" fill="#495057">// 출발점 방향 모두 고려하기</text>
<text x="20" y="55" font-size="16" font-family="monospace" fill="#495057">Node startRight = new Node(0, 0, Dir.RIGHT);</text>
<text x="20" y="80" font-size="16" font-family="monospace" fill="#495057">Node startDown = new Node(0, 0, Dir.DOWN);</text>
<rect x="217" y="39" width="95" height="18" fill="#ffd8a8" opacity="0.7" rx="3" ry="3" />
<rect x="217" y="64" width="90" height="18" fill="#ffd8a8" opacity="0.7" rx="3" ry="3" />
<text x="500" y="45" font-size="14" fill="#495057">← 방향을 함께 저장</text>
<path d="M 315 47 L 480 45" stroke="#fd7e14" stroke-width="1.5" fill="none" marker-end="url(#arrowhead)" />
<text x="500" y="72" font-size="14" fill="#495057">← 두 방향으로 시작</text>
<path d="M 310 72 L 480 72" stroke="#fd7e14" stroke-width="1.5" fill="none" marker-end="url(#arrowhead)" />
</g>
</svg>
이후엔 queue에 Road 객체로서 넣어주고, 다른 BFS 처럼 탐색을 진행하면 된다. Road 객체를 넣는 이유는 노드와 누적 비용 두 정보가 항상 같이 움직일 수 있기 때문이다.
| Road(Node, cost) | 큐에서 꺼내는 순간 “현재 위치 + 지금까지 든 돈” 을 즉시 사용 가능→ 불필요한 맵 조회·계산이 사라져 로직이 한눈에 보인다. |
| Node 만 넣고 dist 테이블에서 비용 다시 읽기 | 매 pop 마다 cost = costs[row][col][dir] 을 찾아야 함→ 코드가 장황해지고, 테이블 오프셋 실수 가능 |
또한 이 문제에서는 뒤로가기와 같은 케이스는 없는데, 향후 필요하다면 Road 안에 필드를 더 넣어
- prev – 경로 복원용 링크
- turnCnt – 코너 개수 별도 집계
같은 확장을 쉽게 할 수도 있다.
3. 첫 번째 예제의 데이터 흐름을 따라가 보자
다음과 같은 첫 번째 예제의 경우 흐름을 따라가보자.
[[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
초기 상태:
- 맵 크기: 3x3
- 시작점: (0,0)
- 목표점: (2,2)
- 모든 칸이 통행 가능(0)
탐색 시작:
- 큐 초기화:
- Node(0,0,RIGHT), 비용 0
- Node(0,0,DOWN), 비용 0
| 0 | 1 | 2 | |
| initial | 0 | – | – |
| – | – | – | |
| – | – | – |
queue에 들어있던 오른쪽 방향의 노드를 꺼낸 다음에는,
- 현재: Node(0,0,RIGHT), 비용 0
- 이동 가능한 다음 노드들:
- Node(0,1,RIGHT): 직선 이동, 비용 +100 = 100
- Node(1,0,DOWN): 코너 이동, 비용 +600 = 600
- Node(-1,0,UP) 및 Node(0,-1,LEFT)는 범위 밖이라 제외
동일하게 아래 방향을 꺼내면,
- 현재: Node(0,0,DOWN), 비용 0
- 이동 가능한 다음 노드들:
- Node(1,0,DOWN): 직선 이동, 비용 +100 = 100
- Node(0,1,RIGHT): 코너 이동, 비용 +600 = 600
즉, 다음과 같은 모습이 될 것이다.
① (0,0,R,0) 팝 → 직선 100 / 코너 600 두 칸 갱신
| 0 | 1 | 2 | |
| step 1 | 0 | 100 | — |
| 600 | — | — | |
| — | — | — |
② (0,0,D,0) 팝 → 직선으로 내려가는 (1,0,D) 의 비용은
currentCost(0) + moveCost(직선 100) = 100
이고, 그 순간 costs[1][0][D] 에는 600 이 들어 있으므로 updateIfCheaper() 가 100 < 600 을 감지해 값을 100 으로 덮어쓴다.
| 0 | 1 | 2 | |
| step 2 | 0 | 100 | — |
| 100 | — | — | |
| — | — | — |
시작점 두 방향을 동시에 넣었기 때문에 “아래로만 갈 수 있는 보드”라도 탐색이 끊기지 않는다.
계속 진행하며 900 원이 확정되는 순간까지의 흐름
| 0 | 1 | 2 | |
| step 3 | 0 | 100 | 200 |
| 600 | 700 | — | |
| — | — | — |
| 0 | 1 | 2 | |
| step 4 | 0 | 100 | 200 |
| 100 | 700 | — | |
| 200 | 800 | — |
| 0 | 1 | 2 | |
| step 5 | 0 | 100 | 200 |
| 600 | 700 | 800 | |
| 700 | 800 | — |
| 0 | 1 | 2 | |
| step 6 (끝) | 0 | 100 | 200 |
| 100 | 700 | 800 | |
| 200 | 800 | 900 |
- (2,2) 칸의 네 방향 값이 {R: 900, D:1000, L:1100, U:1100} 으로 확정
- board.minGoalCost() 가 900 을 반환 → 첫 예제 정답 ✅
최소 비용 경로는 다음과 같다.
(0,0) → (0,1) → (0,2) → (1,2) → (2,2) = 900원
총 비용: 100 + 100 + 600 + 100 = 900원
<!-- 3×3 경주로 – 최소비용 경로(900원) -->
<svg viewBox="0 0 300 300" xmlns="http://www.w3.org/2000/svg">
<!-- 격자 3×3 -->
<defs>
<pattern id="grid" width="100" height="100" patternUnits="userSpaceOnUse">
<path d="M 100 0 L 0 0 0 100" fill="none" stroke="#ccc" stroke-width="1"/>
</pattern>
<marker id="arrow" markerWidth="8" markerHeight="8" refX="7" refY="3.5"
orient="auto" markerUnits="strokeWidth">
<path d="M0,0 L0,7 L7,3.5 z" fill="#2c3e50"/>
</marker>
</defs>
<!-- 배경 격자 -->
<rect width="300" height="300" fill="url(#grid)"/>
<!-- 경로(빨강: 코너, 파랑: 직선) -->
<!-- (0,0) ▶︎ (0,1) ▶︎ (0,2) ▼ (1,2) ▼ (2,2) -->
<g stroke-linecap="round" stroke-width="6" fill="none">
<!-- 직선 3개 -->
<path d="M 50 50 L 150 50" stroke="#2980b9" marker-end="url(#arrow)"/> <!-- 100원 -->
<path d="M 150 50 L 250 50" stroke="#2980b9" marker-end="url(#arrow)"/> <!-- 100원 -->
<path d="M 250 150 L 250 250" stroke="#2980b9" marker-end="url(#arrow)"/> <!-- 100원 -->
<!-- 코너 1개 -->
<path d="M 250 50 L 250 150" stroke="#e74c3c" marker-end="url(#arrow)"/> <!-- 600원 -->
</g>
<!-- 노드 표시 -->
<!-- 시작 -->
<circle cx="50" cy="50" r="8" fill="#27ae60"/>
<text x="50" y="40" text-anchor="middle" font-size="12" fill="#27ae60">Start</text>
<!-- 도착 -->
<circle cx="250" cy="250" r="8" fill="#f39c12"/>
<text x="250" y="240" text-anchor="middle" font-size="12" fill="#f39c12">Goal</text>
<!-- 비용 라벨 -->
<text x="100" y="40" text-anchor="middle" font-size="11" fill="#2980b9">+100</text>
<text x="200" y="40" text-anchor="middle" font-size="11" fill="#2980b9">+100</text>
<text x="265" y="100" text-anchor="start" font-size="11" fill="#e74c3c">+600</text>
<text x="265" y="200" text-anchor="start" font-size="11" fill="#2980b9">+100</text>
<!-- 총 비용 -->
<text x="150" y="285" text-anchor="middle" font-size="14" font-weight="bold">
총 비용 = 900원
</text>
</svg>
🚀 전체 코드
package template.programmers;
import static org.junit.jupiter.api.Assertions.*;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Queue;
import org.junit.jupiter.api.Nested;
import org.junit.jupiter.api.Test;
class Solution {
public int solution(int[][] board) {
Board gameBoard = new Board(board);
return bfs(gameBoard);
}
public int bfs(Board board) {
Queue<Road> queue = new ArrayDeque<>();
Node startRight = new Node(0, 0, Dir.RIGHT);
Node startDown = new Node(0, 0, Dir.DOWN);
board.recordStartCost(startRight);
board.recordStartCost(startDown);
queue.add(new Road(startRight, 0));
queue.add(new Road(startDown, 0));
while (!queue.isEmpty()) {
Road currentRoad = queue.poll();
Node currentNode = currentRoad.node;
int currentCost = currentRoad.accumulatedCost;
if (board.isGoal(currentNode)) {
continue; // 다른 방향이 더 쌀 수도 있으니 계속 탐색
}
for (Node nextNode : currentNode.next(board)) {
int nextCost = currentCost + currentNode.moveCostTo(nextNode);
if (board.updateIfCheaper(nextNode, nextCost)) {
queue.add(new Road(nextNode, nextCost));
}
}
}
return board.minGoalCost();
}
public static class Board {
public int[][] map;
public int N;
public int[][][] costs; // [행][열][방향] = 비용 <- visited 까지 포함
public Board(int[][] arr) {
this.map = arr;
this.N = arr.length;
this.costs = new int[N][N][4];
Arrays.stream(costs).forEach(plane -> Arrays.stream(plane).forEach(line -> Arrays.fill(line, Integer.MAX_VALUE))); // plain: 평면 , line: 1차원 행들
}
public boolean updateIfCheaper(Node node, int cost) {
int dirIndex = node.getDirIndex();
if (cost < costs[node.row][node.col][dirIndex]) {
costs[node.row][node.col][dirIndex] = cost;
return true;
}
return false;
}
public int minGoalCost() {
return Arrays.stream(costs[N - 1][N - 1]).min().orElse(Integer.MAX_VALUE);
}
public boolean inRange(Node p) {
return 0 <= p.row && p.row < N && 0 <= p.col && p.col < N;
}
public boolean canMoveTo(Node p) {
return inRange(p) && map[p.row][p.col] == 0;
}
public boolean isGoal(Node p) {
return p.row == N - 1 && p.col == N - 1;
}
public void recordStartCost(Node startNode) {
updateIfCheaper(startNode, 0);
}
}
/**
* 어느 칸에 어떤 방향으로부터 왔는지 == 위치 + 방향
*/
public static class Node {
public int row;
public int col;
public Dir dir;
public Node(int row, int col, Dir dir) {
this.row = row;
this.col = col;
this.dir = dir;
}
public List<Node> next(Board board) {
List<Node> list = new ArrayList<>(4);
for (Dir nextDir : Dir.values()) {
Node nextNode = nextDir.step(this);
if (board.canMoveTo(nextNode)) {
list.add(nextNode);
}
}
return list;
}
public int moveCostTo(Node nextNode) {
return this.dir.moveCostTo(nextNode.dir);
}
public int getDirIndex() {
return this.dir.ordinal();
}
}
public enum Dir {
UP(-1, 0),
DOWN(1, 0),
LEFT(0, -1),
RIGHT(0, 1);
public final int deltaRow;
public final int deltaCol;
Dir(int deltaRow, int deltaCol) {
this.deltaRow = deltaRow;
this.deltaCol = deltaCol;
}
public Node step(Node node) {
return new Node(node.row + deltaRow, node.col + deltaCol, this);
}
/**
* 180° “후진”은 실제로 탐색 대상이긴 하지만 (네 방향 모두 열어보므로)
* 이미 더 싼 값이 dist에 기록돼 있으면 {@code updateIfCheaper } 단계에서 걸러지므로,
* 즉, “뒤로 한 칸” 갔다가 다시 앞으로 오는 경로는 결국 더 비싸서
* 최종 답에는 포함되지 않으므로
* “축(가로·세로)이 같은가?” 만으로 충분히 판단할 수 있다.
*/
int moveCostTo(Dir next) {
boolean sameAxis = isBothXAxis(next) || isBothYAxis(next);
return sameAxis ? 100 : 100 + 500;
}
private boolean isBothYAxis(Dir next) {
return this.deltaCol == 0 && next.deltaCol == 0;
}
private boolean isBothXAxis(Dir next) {
return this.deltaRow == 0 && next.deltaRow == 0;
}
}
public static class Road {
public Node node;
public int accumulatedCost;
public Road(Node node, int accumulatedCost) {
this.node = node;
this.accumulatedCost = accumulatedCost;
}
}
@Nested
class WordChainTests {
// board result
// [[0,0,0],[0,0,0],[0,0,0]] 900
// [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] 3800
// [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] 2100
// [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] 3200
@Test
void testCase1() {
int[][] board = {
{0, 0, 0},
{0, 0, 0},
{0, 0, 0}
};
int expected = 900;
assertEquals(expected, solution(board));
}
@Test
void testCase2() {
int[][] board = {
{0, 0, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 1, 0, 0},
{1, 0, 0, 0, 0, 0, 0, 0}
};
int expected = 3800;
assertEquals(expected, solution(board));
}
@Test
void testCase3() {
int[][] board = {
{0, 0, 1, 0},
{0, 0, 0, 0},
{0, 1, 0, 1},
{1, 0, 0, 0}
};
int expected = 2100;
assertEquals(expected, solution(board));
}
}
}
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 타겟 넘버 (3가지 풀이 방식, DFS, 트리, 그리고 수학적 공식을 이용한 최적화) (0) | 2025.05.24 |
|---|---|
| [프로그래머스] 두개 뽑아서 더하기 (자바 & 코틀린 풀이) (0) | 2025.05.21 |
| [프로그래머스] 네트워크 (자바 풀이) (0) | 2025.04.29 |
| [프로그래머스] 표 편집 (2021 카카오 채용연계형 인텁십, 자바 풀이) (0) | 2024.09.30 |
| [프로그래머스] 두 개 뽑아서 더하기 (0) | 2024.09.15 |



