
https://school.programmers.co.kr/learn/courses/30/lessons/81303
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
📌 문제
업무용 소프트웨어를 개발하는 니니즈웍스의 인턴인 앙몬드는 명령어 기반으로 표의 행을 선택, 삭제, 복구하는 프로그램을 작성하는 과제를 맡았습니다. 세부 요구 사항은 다음과 같습니다
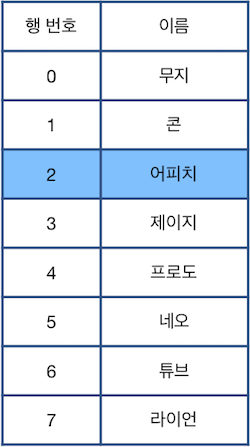
위 그림에서 파란색으로 칠해진 칸은 현재 선택된 행을 나타냅니다. 단, 한 번에 한 행만 선택할 수 있으며, 표의 범위(0행 ~ 마지막 행)를 벗어날 수 없습니다. 이때, 다음과 같은 명령어를 이용하여 표를 편집합니다.
"U X": 현재 선택된 행에서 X칸 위에 있는 행을 선택합니다.
"D X": 현재 선택된 행에서 X칸 아래에 있는 행을 선택합니다.
"C" : 현재 선택된 행을 삭제한 후, 바로 아래 행을 선택합니다. 단, 삭제된 행이 가장 마지막 행인 경우 바로 윗 행을 선택합니다.
"Z" : 가장 최근에 삭제된 행을 원래대로 복구합니다. 단, 현재 선택된 행은 바뀌지 않습니다.
예를 들어 위 표에서 "D 2"를 수행할 경우 아래 그림의 왼쪽처럼 4행이 선택되며, "C"를 수행하면 선택된 행을 삭제하고, 바로 아래 행이었던 "네오"가 적힌 행을 선택합니다(4행이 삭제되면서 아래 있던 행들이 하나씩 밀려 올라오고, 수정된 표에서 다시 4행을 선택하는 것과 동일합니다).
처음 표의 행 개수를 나타내는 정수 n, 처음에 선택된 행의 위치를 나타내는 정수 k, 수행한 명령어들이 담긴 문자열 배열 cmd가 매개변수로 주어질 때, 모든 명령어를 수행한 후 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 O, 삭제된 행은 X로 표시하여 문자열 형태로 return 하도록 solution 함수를 완성해주세요.
⚔ 제한 사항
제한사항
- 5 ≤ n ≤ 1,000,000
- 0 ≤ k < n
- 1 ≤ cmd의 원소 개수 ≤ 200,000
- cmd의 각 원소는 "U X", "D X", "C", "Z" 중 하나입니다.- X는 1 이상 300,000 이하인 자연수이며 0으로 시작하지 않습니다.
- X가 나타내는 자연수에 ',' 는 주어지지 않습니다. 예를 들어 123,456의 경우 123456으로 주어집니다.
- cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.
- 표의 모든 행을 제거하여, 행이 하나도 남지 않는 경우는 입력으로 주어지지 않습니다.
- 본문에서 각 행이 제거되고 복구되는 과정을 보다 자연스럽게 보이기 위해 "이름" 열을 사용하였으나, "이름"열의 내용이 실제 문제를 푸는 과정에 필요하지는 않습니다. "이름"열에는 서로 다른 이름들이 중복없이 채워져 있다고 가정하고 문제를 해결해 주세요.
- 표의 범위를 벗어나는 이동은 입력으로 주어지지 않습니다.
- 원래대로 복구할 행이 없을 때(즉, 삭제된 행이 없을 때) "Z"가 명령어로 주어지는 경우는 없습니다.
- 정답은 표의 0행부터 n - 1행까지에 해당되는 O, X를 순서대로 이어붙인 문자열 형태로 return 해주세요.
정확성 테스트 케이스 제한 사항- 5 ≤ n ≤ 1,000
- 1 ≤ cmd의 원소 개수 ≤ 1,000
효율성 테스트 케이스 제한 사항- 주어진 조건 외 추가 제한사항 없습니다.
입출력 예시
| n | k | cmd | result |
| 8 | 2 | ["D 2","C","U 3","C","D 4","C","U 2","Z","Z"] | "OOOOXOOO" |
| 8 | 2 | ["D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"] | "OOXOXOOO" |
👀 문제 해석
이 문제는 명령어로 표의 행을 관리하는 프로그램을 구현하는 과제이다. 주어진 명령어를 통해 행을 선택, 삭제, 복구한 후 최종적으로 표의 상태를 반환하는 것이 목표다.
핵심 요구 사항은 네 가지다.
1. "U X" 및 "D X" 명령으로 선택된 행을 위아래로 이동.
2. "C" 명령으로 선택된 행을 삭제하고, 그 아래 또는 위 행을 선택.
3. "Z" 명령으로 최근 삭제된 행을 복구.
4. 명령어 처리 후 남은 행은 'O', 삭제된 행은 'X'로 표시된 결과 반환.
이 문제는 자료구조 문제로, 특히 스택과 연결 리스트를 활용해 효율적으로 처리할 수 있다. 스택은 삭제된 행을 기록하고, 연결 리스트는 행 이동과 삭제 복구를 빠르게 처리할 수 있도록 돕는다. 표의 크기가 최대 1,000,000에 이를 수 있기 때문에, 시간 복잡도 최적화가 중요한 문제이다.
다만, 처음 접근시에는 연결 리스트가 아니라 배열을 사용했고, 실패하는 과정이 있었다.
🔎 실패한 접근
이 문제는 여러 명령어가 복잡하게 얽혀 있어, 각 기능을 독립적으로 처리하는 구조를 만드는 것이 중요할 것으로 판단했다. 따라서 애초에 문제의 요구되는 기능 구현에 대해 객체 지향적으로 풀이하면 깔끔하면서도 정돈된 코드를 작성할 수 있을 것으로 생각했다.
이를 위해 명령어 처리와 표 상태 유지를 위한 객체를 분리하여 각자의 책임을 명확히 할 필요가 있다. 그렇다면 이때 필요한 객체는 무엇일까?
표를 나타내는 Table과 명령을 처리하는 Cmd 객체가 가능할 것이다. Table 객체는 표의 상태 관리와 명령 처리, Cmd 객체는 명령어를 해석하고 실행하는 역할을 담당한다. 해당 객체들은 다음과 같은 요소를 갖는다.
public static class Table {
private boolean[] rows;
private int currentIndex;
private Stack<Integer> backupRows;
}
1. rows: boolean[] 배열로 각 행의 삭제 여부를 저장. 배열의 크기는 표의 전체 행 수(n)이며, 삭제된 행은 false, 유지된 행은 true로 표기.
2. currentIndex: 현재 선택된 행의 인덱스를 저장하는 변수. 이동 명령(U, D)을 처리할 때 사용.
3. backupRows: 스택(Stack)으로 삭제된 행의 인덱스를 기록. 복구 명령(Z)을 처리할 때 사용.
그리고 테이블을 이동하는 연산들이 필요하다.
public void handleCommand(Cmd cmd) {
switch (cmd.명령어) {
case 올라가기:
moveUp(cmd.이동칸수);
break;
case 내려가기:
moveDown(cmd.이동칸수);
break;
case 행지우기:
deleteRow();
break;
case 되돌리기:
undoDelete();
break;
}
}
// 현재 행에서 X칸 위로 이동 -> 삭제된 행은 건너뜀
private void moveUp(int x) {
int count = 0;
while (count < x) {
currentIndex--;
if (isNotDeleted()) {
count++;
}
}
}
// 현재 행에서 X칸 아래로 이동 -> 삭제된 행은 건너뜀
private void moveDown(int x) {
int count = 0;
while (count < x) {
currentIndex++;
if (isNotDeleted()) {
count++;
}
}
}
private boolean isNotDeleted() {
return rows[currentIndex];
}
// 현재 선택된 행을 삭제하고 바로 아래 행 선택 (마지막 행인 경우는 위로)
private void deleteRow() {
backupRows.push(currentIndex);
rows[currentIndex] = false;
if (isCurrentIndexLast()) {
moveUp(1);
} else {
moveDown(1);
}
}
private boolean isCurrentIndexLast() {
return currentIndex == rows.length - 1;
}
private void undoDelete() {
if (!backupRows.isEmpty()) {
int restoredIndex = backupRows.pop();
rows[restoredIndex] = true; // 행 복구
}
}
// 최종 상태 문자열 반환 -> 삭제되지 않은 행은 O, 삭제된 행은 X
public String getFinalState() {
StringBuilder sb = new StringBuilder();
for (boolean row : rows) {
sb.append(row ? "O" : "X");
}
return sb.toString();
}
Cmd 객체는 명령어를 해석하고, 그에 맞는 동작을 실행하는 역할을 한다.
public static class Cmd {
public 명령어타입 명령어;
public int 이동칸수;
public Cmd(String cmd) {
if (cmd.startsWith("Z")) {
this.명령어 = 명령어타입.되돌리기;
} else if (cmd.startsWith("C")) {
this.명령어 = 명령어타입.행지우기;
} else if (cmd.startsWith("U")) {
this.명령어 = 명령어타입.올라가기;
this.이동칸수 = Integer.parseInt(cmd.split(" ")[1]);
} else if (cmd.startsWith("D")) {
this.명령어 = 명령어타입.내려가기;
this.이동칸수 = Integer.parseInt(cmd.split(" ")[1]);
}
}
public enum 명령어타입 {
되돌리기("Z"),
행지우기("C"),
올라가기("U"),
내려가기("D");
private final String cmd;
명령어타입(String cmd) {
this.cmd = cmd;
}
}
}
이때, 테이블을 어떻게 관리하느냐가 핵심이다. 위의 코드에서처럼 처음 접근에서는 배열을 사용하는 방식이다. 배열은 각 행의 상태를 빠르게 조회하고 수정하는 데 유리하다. boolean[] rows 배열을 통해 행의 존재 여부를 기록하고, 삭제된 행은 false, 남아 있는 행은 true로 표시한다. 이때 행을 삭제한 후 복구하는 로직에서는 삭제된 행의 인덱스를 기억해두는 스택(Stack)을 사용했다.
이 과정의 로직은 다음과 같다.
1. 배열을 이용해 각 행의 상태를 관리하고, 삭제된 행의 복구를 위해 스택을 사용한다.
2. "U X" 및 "D X" 명령어는 단순히 인덱스를 조정하며, 삭제된 행은 건너뛴다.
3. "C" 명령어는 해당 행을 삭제하고, 삭제된 행의 인덱스를 스택에 저장한다.
4. "Z" 명령어는 스택에서 인덱스를 꺼내 복구한다.
이 방식의 결과는 어떨까?
일단 샘플 테스트는 통과한다.

채점을 시작하면 다음과 같이 실패해서 '실패'를 받는다!
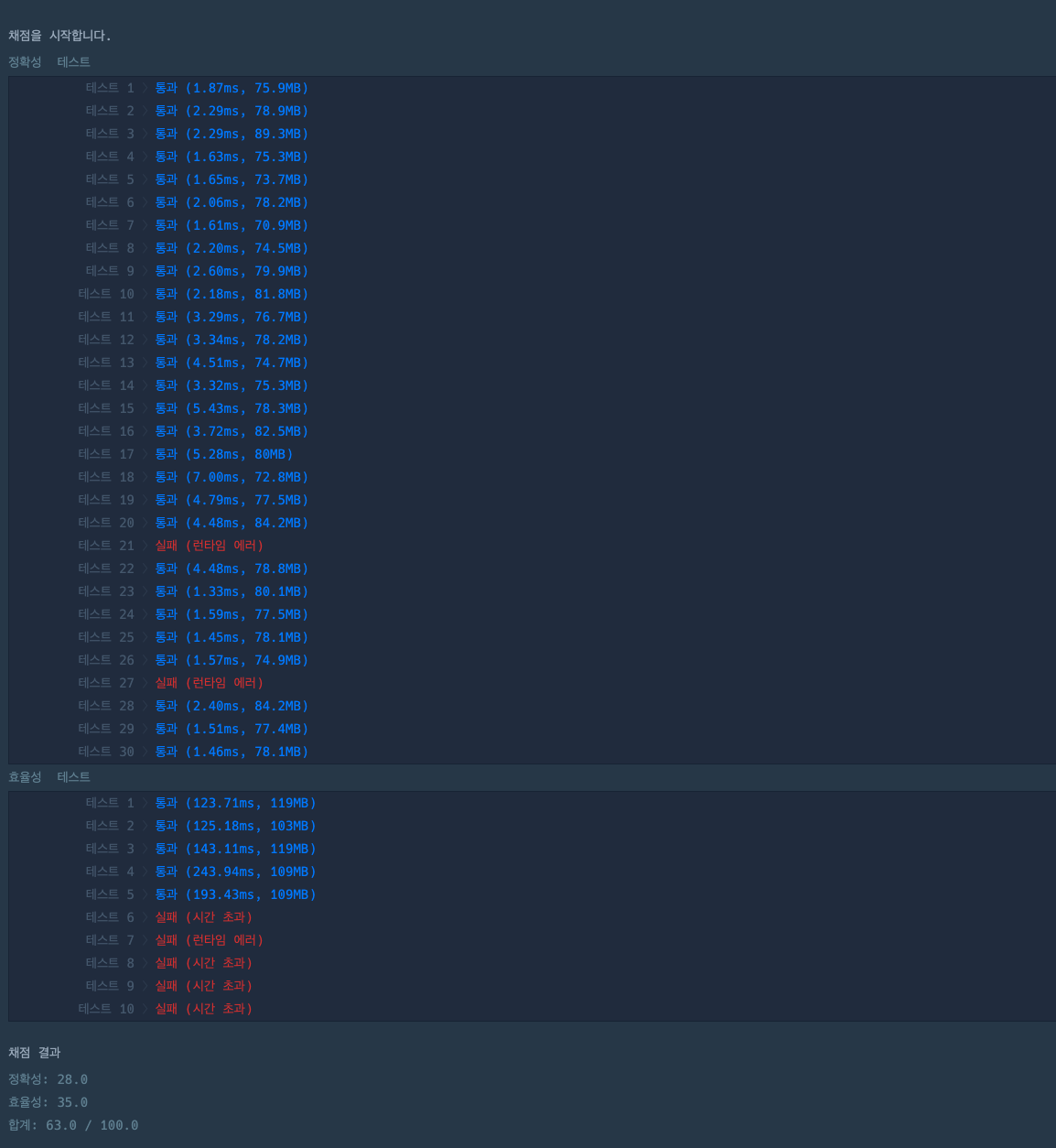
효율성이 실패하는 것은 그렇다쳐도 정확성에서 실패하는 21번과 27번은 도대체 무엇일까?
이 두 케이스를 정말 찾고 싶어서 여러 가지 시도를 해보았는데도 결국 찾지는 못했다.
@Nested
class SolutionTestCases {
@Test
public void testValidCases() {
Solution solution = new Solution();
// 첫 번째 테스트 케이스
String[] cmd1 = {"D 2", "C", "U 3", "C", "D 4", "C", "U 2", "Z", "Z"};
String result1 = solution.solution(8, 2, cmd1);
Assertions.assertEquals("OOOOXOOO", result1, "첫 번째 테스트 실패");
// 두 번째 테스트 케이스
String[] cmd2 = {"D 2", "C", "U 3", "C", "D 4", "C", "U 2", "Z", "Z", "U 1", "C"};
String result2 = solution.solution(8, 2, cmd2);
Assertions.assertEquals("OOXOXOOO", result2, "두 번째 테스트 실패");
String[] cmd3 = {"C"};
String result3 = solution.solution(8, 7, cmd3);
Assertions.assertEquals("OOOOOOOX", result3, "3번째 테스트 실패");
}
@Test
public void testValidCases2() {
Solution solution = new Solution();
String[] cmd4 = {"C"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XOOOO", result4, "4번째 테스트 실패 ");
}
@Test
public void testValidCases3() {
Solution solution = new Solution();
String[] cmd4 = {"C", "C", "C", "C"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XXXXO", result4, "4번째 테스트 실패 ");
}
@Test
public void testValidCases4() {
Solution solution = new Solution();
String[] cmd4 = {"C", "C", "C", "C", "Z"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XXXOO", result4, "4번째 테스트 실패 ");
}
@Test
public void testValidCases5() {
Solution solution = new Solution();
String[] cmd4 = {"C", "C", "C", "C", "Z", "U 1"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XXXOO", result4, "4번째 테스트 실패 ");
}
@Test
public void testValidCases6() {
Solution solution = new Solution();
String[] cmd4 = {"C", "C", "C", "C", "Z", "C"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XXXOX", result4, "4번째 테스트 실패 ");
}
@Test
public void testValidCases7() {
Solution solution = new Solution();
String[] cmd4 = {"C", "C", "C", "C", "Z", "C", "Z"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XXXOO", result4, "4번째 테스트 실패 ");
}
@Test
public void testValidCases8() {
Solution solution = new Solution();
String[] cmd4 = {"C", "C", "C", "C", "Z", "C", "Z", "C"};
String result4 = solution.solution(5, 0, cmd4);
Assertions.assertEquals("XXXXO", result4, "4번째 테스트 실패 ");
}
}
추론으로서 생각해볼 수 있는 점은 데이터 셋이 많아서 작동 과정에서 런타임 에러가 발생한 것은 아닐런지... 그냥 추측만 해본다. 아무리 찾아도 반례를 찾을 수가 없다 ㅠㅠ
어찌됐든 배열을 사용하는 방식으로는 효율성에서 실패하기 때문에 로직을 개선해야 한다.
접근을 다르게 해야만 풀 수 있다. 어떻게 해야할까?
💡 풀이 코드
배열을 사용한 방식에서는 행 삭제 및 복구를 위한 상태 저장과 이동 처리를 위해 boolean[] 배열과 스택을 사용한다. 그러나 효율성 측면에서 한계가 있다. 주어진 문제에서 표의 최대 값은 1,000,000이다. 이때, 다음과 같은 예를 들어보자.
배열 기반 접근의 비효율성
예를 들어, 표의 크기가 1,000,000인 상태에서, 첫 번째와 마지막 행을 제외한 모든 행을 삭제했다고 가정해 보자. 이 상태에서 첫 번째 행에서 마지막 행으로 이동하려면, "D 999,999" 명령을 실행하게 된다. 배열 기반 방식에서는 삭제된 행을 모두 건너뛰며 이동해야 하기 때문에, 각 인덱스를 탐색하는 비용이 발생한다. 삭제된 행이 많을 경우, 이 과정에서 매우 큰 비효율이 발생한다.
// 현재 행에서 X칸 아래로 이동 -> 삭제된 행은 건너뜀
private void moveDown(int x) {
int count = 0;
while (count < x) {
currentIndex++;
if (isNotDeleted()) {
count++;
}
}
}
위 코드에서 moveDown 함수는 currentIndex를 증가시키며 X칸만큼 이동하는데, 삭제된 행은 건너뛰어야 한다. 첫 번째와 마지막 행만 남겨두고 나머지 행이 모두 삭제된 경우, 이 함수는 999,998개의 삭제된 행을 하나씩 확인하며 건너뛰어야 한다. 이때, 삭제 여부를 검사하는 isNotDeleted() 함수가 불필요하게 호출되며, 이때 시간 복잡도가 O(n)이 된다. 삭제된 행이 많을수록 이동에 필요한 시간이 급격히 증가한다.
예를 들어, 첫 번째 행에서 마지막 행으로 이동하려면 다음과 같은 과정을 거치게 된다.
1. 첫 번째 행에서 시작.
2. 두 번째 행이 삭제되었는지 확인 → 삭제되었음.
3. 세 번째 행이 삭제되었는지 확인 → 삭제되었음.
4. ...
5. 마지막 행(1,000,000번째 행)에 도달할 때까지 위 과정을 반복.
삭제된 행을 계속해서 확인하며 이동한다. 삭제된 행이 많아질수록 이동에 걸리는 시간은 매우 비효율적으로 늘어난다.

명령어의 개수(cmd의 최대 개수)는 최대 200,000개이므로, 20만 개의 커맨드에서 대해서 n개의 반복 연산이 선형적으로 증가하므로, 따라서 최종 시간 복잡도는 cmd를 C라고 할 때, O(C*N)이 되며, 이는 총 200억 번의 연산으로 계산된다.
여기서 중요한 점은, 실제 이동 거리는 2이지만, 100만 개의 삭제된 false 요소를 전부 탐색한다는 점이다.
따라서 배열이 아닌 다른 자료구조가 필요하다.
연결 리스트로 개선한 방식
연결 리스트를 고려할 수 있다. 왜일까?
연결 리스트는 각 행이 이전, 다음 행을 가리키는 구조로, 삭제된 행을 빠르게 건너뛸 수 있다. 즉, 삭제된 행을 확인하는 과정 없이 O(1) 시간에 다음 유효한 행으로 이동 가능하다. 따라서 이동 및 삭제 복구 시 비효율을 줄일 수 있어, 시간 복잡도를 획기적으로 개선할 수 있다.
0. Node로 연결리스트의 구조 만들기
연결 리스트의 핵심은 Node를 사용하여 각 행을 연결하는 것이다. 따라서 Node 객체가 필요하다. Node는 세 가지 정보를 가진다.
- 현재 행의 인덱스 (index)
- 이전 행의 인덱스 (prev)
- 다음 행의 인덱스 (next)
이 구조는 행을 삭제할 때 이전 행과 다음 행을 연결함으로써, 삭제된 행을 건너뛰는 연산을 빠르게 처리할 수 있다. 또한, 복구할 때는 다시 연결을 복원하여 삭제 전의 상태로 쉽게 돌아갈 수 있다. 이를 통해 삭제와 복구 과정에서 발생할 수 있는 성능 문제를 O(1)로 해결할 수 있다.
private static class Node {
int index;
int prev;
int next;
Node(int index, int prev, int next) {
this.index = index;
this.prev = prev;
this.next = next;
}
}
1. prev[]와 next[] 배열을 사용
기존 배열 방식에서는 boolean[] 배열을 사용해 행의 삭제 여부를 기록하고, 삭제된 행을 복구할 때마다 배열을 순회해야 한다. 그러나 연결 리스트 방식에서는 prev[]와 next[] 배열을 사용하여 각 행이 이전 행과 다음 행의 인덱스를 가리키도록 할 수 있다.
- prev[i]는 행 i의 이전 행 인덱스를,
- next[i]는 행 i의 다음 행 인덱스를 저장한다.
이 방식을 사용하면 삭제된 행을 확인할 필요 없이, 곧바로 연결된 유효한 행으로 이동할 수 있다.
// 초기화 - 연결 리스트의 구조를 설정
for (int i = 0; i < n; i++) {
prev[i] = i - 1;
next[i] = i + 1;
}
next[n - 1] = -1; // 마지막 행의 다음은 없음
2. 이동 명령의 처리
이동 명령은 배열 방식에서는 삭제된 행을 일일이 확인해야 했다. 연결 리스트 방식에서는 prev[]와 next[] 배열을 따라 이동하면 된다. 예를 들어, "U X" 또는 "D X" 명령어는 X칸만큼 이전 또는 다음 노드를 탐색하여 바로 이동할 수 있다.
// 위로 X칸 이동
private void moveUp(int x) {
for (int i = 0; i < x; i++) {
currentIndex = prev[currentIndex]; // 바로 이전 행으로 이동
}
}
// 아래로 X칸 이동
private void moveDown(int x) {
for (int i = 0; i < x; i++) {
currentIndex = next[currentIndex]; // 바로 다음 행으로 이동
}
}
배열과의 차이점을 다시 한번 상기시켜보자.
배열의 경우, 삭제된 행을 하나씩 확인하면서 이동해야 한다. 즉, boolean[] 배열에서 삭제 여부를 확인하는 연산이 필요하고, 삭제된 행이 많을 경우 삭제된 행을 건너뛰는 데 O(n) 시간이 소요된다. 예를 들어, "D X" 명령을 수행할 때, 현재 위치에서 X칸 아래로 이동해야 하지만, 삭제된 행이 있으면 계속 확인하면서 건너뛰어야 한다.
그런데 연결 리스트 방식에서는 각 행이 이전 행(prev[])과 다음 행(next[])을 직접 가리키고 있다. 즉, 삭제된 것은 실제로 삭제되어 있다. 이것이 핵심이다. 단순히 next[] 배열을 따라 이동하므로 O(1) 시간에 삭제된 행을 건너뛸 수 있다. 따라서 삭제 여부를 확인하는 연산이 필요 없기 때문에, 이동 과정에서 삭제된 행의 수와 관계없이 항상 O(X) 시간만 소요된다.
3. 행 삭제와 복구
이제 삭제와 복구 과정을 살펴보자.
행을 삭제할 때, 배열에서는 해당 행을 false로 표시하고 스택에 기록했지만, 연결 리스트 방식에서는 삭제된 행의 prev[]와 next[]를 조정하여 삭제된 행을 연결에서 분리한다. 삭제된 행의 이전 노드와 다음 노드를 직접 연결하여 삭제된 행을 건너뛰도록 만든다. 이 과정은 O(1) 시간 복잡도로 처리된다.
// 현재 선택된 행을 삭제하고 바로 다음 행 선택
private void deleteRow() {
backupRows.push(new Node(currentIndex, prev[currentIndex], next[currentIndex]));
// 이전 노드와 다음 노드를 연결
if (prev[currentIndex] != -1) {
next[prev[currentIndex]] = next[currentIndex];
}
if (next[currentIndex] != -1) {
prev[next[currentIndex]] = prev[currentIndex];
}
// 현재 인덱스 업데이트 (다음 행으로 이동, 없으면 이전 행으로)
if (next[currentIndex] != -1) {
currentIndex = next[currentIndex];
} else {
currentIndex = prev[currentIndex];
}
}
이 부분이 핵심이기 때문에, 작동 과정을 좀 더 상세히 살펴보자.
표의 행이 다음과 같이 구성되어 있다고 가정하자.
[0] <-> [1] <-> [2] <-> [3] <-> [4] <-> [5]
여기서 [2]번 행을 삭제하는 상황을 살펴보자. 삭제된 행 [2]를 리스트에서 제거하고, [1]번 행과 [3]번 행을 서로 연결해야 한다.
1. 삭제할 행의 정보를 저장:
- 먼저 삭제할 행 [2]의 prev와 next를 저장한다.
- 이 정보는 복구할 때 필요하기 때문에, 스택에 이 정보를 저장한다.
backupRows.push(new Node(currentIndex, prev[currentIndex], next[currentIndex]));
- 여기서 currentIndex는 삭제할 행인 [2]이고, 이 행의 prev는 [1], next는 [3]이 된다.
2. 이전 노드와 다음 노드 연결:
- [2]번 행을 삭제하기 위해, [1]번 행과 [3]번 행을 연결해야 한다.
if (prev[currentIndex] != -1) {
next[prev[currentIndex]] = next[currentIndex]; // [1].next = [3]
}
if (next[currentIndex] != -1) {
prev[next[currentIndex]] = prev[currentIndex]; // [3].prev = [1]
}
- [1]번 행의 next를 [3]번 행으로 변경: next[1] = 3
- [3]번 행의 prev를 [1]번 행으로 변경: prev[3] = 1
- 결과적으로, [2]번 행은 리스트에서 완전히 분리된다.
[0] <-> [1] <-> [3] <-> [4] <-> [5]
3. 현재 선택된 행을 업데이트:
- 마지막으로, 삭제된 행 다음에 선택할 행을 업데이트해야 한다. [2]번 행을 삭제했기 때문에, 다음 행인 [3]번을 선택하거나, 마지막 행을 삭제한 경우라면 이전 행으로 이동한다.
if (next[currentIndex] != -1) {
currentIndex = next[currentIndex]; // [3]을 선택
} else {
currentIndex = prev[currentIndex]; // 마지막 행이라면 [1]을 선택
}
이 과정은 삭제된 행의 연결만 조정하고, 추가적인 탐색 없이 이전 노드와 다음 노드를 즉시 연결하기 때문에 O(1) 시간 복잡도로 처리된다는 것이 핵심이다.
이제 스택에 저장해둔 삭제된 행의 정보를 복원하는 것을 살펴보자.
복구할 때는 스택에서 삭제된 행의 정보를 꺼내어, 이전 상태로 연결을 복원한다.
private void undoDelete() {
if (!backupRows.isEmpty()) {
Node node = backupRows.pop();
// 이전 노드와 다음 노드의 연결 복구
if (node.prev != -1) {
next[node.prev] = node.index; // [1].next = [2]
}
if (node.next != -1) {
prev[node.next] = node.index; // [3].prev = [2]
}
}
}
예를 들어, 삭제된 [2]번 행을 복구해보자. [1]번 행의 next를 [2]로, [3]번 행의 prev를 [2]로 다시 연결한다. 복구 후의 리스트는 다시 원래 상태로 돌아간다.
[0] <-> [1] <-> [2] <-> [3] <-> [4] <-> [5]
이 과정을 통해 삭제와 복구 모두 O(1)로 처리되어, 효율적인 연산이 가능하다.
4. 최종 결과 반환
이제 마지막으로 답안을 제출하는 부분을 살펴보자.
이미 객체에서 연결리스트를 답안으로 갖고 있기 때문에 형식만 맞춰주면 된다.
삭제되지 않은 행은 'O'로 표시하고, 삭제된 행은 'X'로 표시한 최종 결과를 반환하는 과정에서도 연결 리스트를 순차적으로 탐색하여 처리한다.
public String getFinalState() {
StringBuilder sb = new StringBuilder();
char[] result = new char[n];
Arrays.fill(result, 'X');
// 첫 번째 행부터 차례대로 순회하면서 삭제되지 않은 행 표시
int idx = currentIndex;
while (prev[idx] != -1) {
idx = prev[idx];
}
while (idx != -1) {
result[idx] = 'O';
idx = next[idx];
}
return new String(result);
}
🚀 최종 제출 코드
import java.util.*;
class Solution {
public String solution(int n, int k, String[] cmds) {
Table table = new Table(n, k);
for (String cmd : cmds) {
table.handleCommand(new Cmd(cmd));
}
return table.getFinalState();
}
public static class Table {
private int n;
private int currentIndex;
private int[] prev;
private int[] next;
private Stack<Node> backupRows;
public Table(int totalRows, int startIndex) {
this.n = totalRows;
this.currentIndex = startIndex;
this.prev = new int[n];
this.next = new int[n];
this.backupRows = new Stack<>();
for (int i = 0; i < n; i++) {
prev[i] = i - 1;
next[i] = i + 1;
}
next[n - 1] = -1;
}
public void handleCommand(Cmd cmd) {
switch (cmd.명령어) {
case 올라가기:
moveUp(cmd.이동칸수);
break;
case 내려가기:
moveDown(cmd.이동칸수);
break;
case 행지우기:
deleteRow();
break;
case 되돌리기:
undoDelete();
break;
}
}
// 현재 행에서 X칸 위로 이동
private void moveUp(int x) {
for (int i = 0; i < x; i++) {
currentIndex = prev[currentIndex];
}
}
// 현재 행에서 X칸 아래로 이동
private void moveDown(int x) {
for (int i = 0; i < x; i++) {
currentIndex = next[currentIndex];
}
}
// 현재 선택된 행을 삭제하고 바로 아래 행 선택 (마지막 행인 경우는 위로)
private void deleteRow() {
backupRows.push(new Node(currentIndex, prev[currentIndex], next[currentIndex]));
// 이전 노드와 다음 노드의 연결을 변경
if (prev[currentIndex] != -1) {
next[prev[currentIndex]] = next[currentIndex];
}
if (next[currentIndex] != -1) {
prev[next[currentIndex]] = prev[currentIndex];
}
// 현재 인덱스 업데이트
if (next[currentIndex] != -1) {
currentIndex = next[currentIndex];
} else {
currentIndex = prev[currentIndex];
}
}
private void undoDelete() {
if (!backupRows.isEmpty()) {
Node node = backupRows.pop();
// 이전 노드와 다음 노드의 연결을 복구
if (node.prev != -1) {
next[node.prev] = node.index;
}
if (node.next != -1) {
prev[node.next] = node.index;
}
}
}
// 최종 상태 문자열 반환 -> 삭제되지 않은 행은 O, 삭제된 행은 X
public String getFinalState() {
StringBuilder sb = new StringBuilder();
char[] result = new char[n];
Arrays.fill(result, 'X');
int idx = currentIndex;
while (prev[idx] != -1) {
idx = prev[idx];
}
while (idx != -1) {
result[idx] = 'O';
idx = next[idx];
}
return new String(result);
}
private static class Node {
int index;
int prev;
int next;
Node(int index, int prev, int next) {
this.index = index;
this.prev = prev;
this.next = next;
}
}
}
public static class Cmd {
public 명령어타입 명령어;
public int 이동칸수;
public Cmd(String cmd) {
if (cmd.startsWith("Z")) {
this.명령어 = 명령어타입.되돌리기;
} else if (cmd.startsWith("C")) {
this.명령어 = 명령어타입.행지우기;
} else if (cmd.startsWith("U")) {
this.명령어 = 명령어타입.올라가기;
this.이동칸수 = Integer.parseInt(cmd.split(" ")[1]);
} else if (cmd.startsWith("D")) {
this.명령어 = 명령어타입.내려가기;
this.이동칸수 = Integer.parseInt(cmd.split(" ")[1]);
}
}
public enum 명령어타입 {
되돌리기("Z"),
행지우기("C"),
올라가기("U"),
내려가기("D");
private final String cmd;
명령어타입(String cmd) {
this.cmd = cmd;
}
}
}
}

'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 두 개 뽑아서 더하기 (0) | 2024.09.15 |
|---|---|
| [프로그래머스] 진료 순서 정하기 - 5가지 방식의 자바 풀이 (0) | 2024.04.21 |
| [프로그래머스/자바] 옹알이 (1) - 두 가지 풀이 방식 (0) | 2024.01.11 |
| [백준/자바] 2775 부녀회장이 될테야 (1) | 2022.12.01 |
| [프로그래머스/파이썬] 레벨 0 피자 나눠 먹기 2 (0) | 2022.10.13 |



