1. 집합(Set)과 상호배타적(Disjoint) 집합이란?
1) 집합(Set)이란?
수학에서 집합(Set) 이란, 어떠한 조건을 만족하는 원소(요소)들의 모임을 의미한다.
알고리즘/자료구조 영역에서도 “중복을 허용하지 않는 원소의 모임”으로 흔히 다루어진다.
집합의 표기
- 일반적으로 중괄호(
{ })로 감싸서 표현한다. - 예:
- \( A = \{1, 2, 3\} \)
- \( B = \{2, 4, 6, 8\} \)
집합의 특징
- 원소의 중복을 허용하지 않는다.
\( \{1,1,2\} \)는 집합 내에서 1이 하나만 존재하므로, 결국 \( \{1,2\} \)와 동일. - 원소들의 순서는 상관이 없다.
\( \{2,4,6\} \)과 \( \{4,6,2\} \)는 집합으로서는 동일. - 원소가 특정 조건을 만족하면 포함되고, 만족하지 않으면 포함되지 않는다.
부분집합(Subset)과 진부분집합(Proper Subset)
- 부분집합: \( A \subseteq B \)는 A의 모든 원소가 B에 속할 때 참.
- 진부분집합: \( A \subset B \)는 A가 B의 부분집합이면서, A ≠ B일 때 성립.
2) 상호배타적(Disjoint) 집합이란?
상호배타적 집합(Disjoint Set) 은 두 집합이 공통 원소를 전혀 갖지 않는 경우를 말한다.
- 예:
- \( A = \{1, 2, 3\} \)
- \( B = \{4, 5, 6\} \)
이 때, A와 B는 공통 원소가 없으므로 상호배타적 집합이다.
상호배타적 집합의 수학적 표현
- \( A \cap B = \emptyset \) (A와 B의 교집합이 공집합이면 상호배타적)
여러 개의 집합에서의 상호배타성
- 세 집합 \( A, B, C \) 가 전부 상호배타적이려면
\( A \cap B = \emptyset, B \cap C = \emptyset, A \cap C = \emptyset \)
이 모두 만족해야 한다.
3) 어디에 쓸까?
집합이라고 하면 조금 추상적으로 느껴질 수 있지만, 사실 일상 속 곳곳에서 쉽게 찾아볼 수 있는 개념이다.
예를 들어, 소셜 미디어에서 여러 해시태그를 붙여서 글을 올린다거나, 친구 목록을 관리한다거나 할 때도 “집합”과 “상호배타적(서로 겹치지 않는) 집합” 개념을 유용하게 사용할 수 있다.

Q1. 알고리즘에서 왜 집합을 배울까?
집합은 “중복이 없는 원소들의 모임” 이라는 특징을 가지고 있다.
- 예를 들어, 어떤 문제를 풀 때 데이터 안에 중복된 값들이 너무 많으면 처리가 불편해질 것이다. 이럴 때 집합 자료구조를 사용하면, 중복된 원소들은 알아서 제거되고 유일한 원소들만 남아 효율적인 처리가 가능하다.
- 또한 “두 집합이 교집합을 갖는지(겹치는 원소가 있는지) 없는지”를 빠르게 확인할 수 있다.
- 상호배타적(Disjoint) 집합인 경우, 교집합이 없으므로 손쉽게 “겹치는 것이 전혀 없다는” 결론을 낼 수 있다.
Q2. 일상에서 집합이 어디에 숨어있을까?
많은 예시가 있지만, 여기서는 대표적으로 해시태그와 친구 목록을 꼽아볼 수 있겠다.
1) 사례 1: 해시태그(Hashtag) 예시
- 인스타그램이나 트위터 등에서 글을 올릴 때, 글의 특징을 표현하기 위해 #맛집, #주말, #파스타와 같은 해시태그를 쓰곤 한다.
- 한 게시물에 달린 해시태그들의 모임을 “집합”으로 볼 수 있다.
- 예를 들어,
\[
\text{게시물}_1\text{ 해시태그} = \{ \#맛집,\, \#파스타,\, \#주말 \}
\]
\[
\text{게시물}_2\text{ 해시태그} = \{ \#맛집,\, \#데이트 \}
\]
┌───────┐ ┌────────┐
│게시물1 │ │게시물2 │
└───┬───┘ └───┬────┘
│ │
▼ ▼
┌───────────────────────────┐
│ #맛집 #파스타 │ → {#맛집, #파스타, #주말}
│ #주말 │ {#맛집, #데이트}
│ │
└───────────────────────────┘
게시물1과 게시물2 모두 #맛집을 갖고 있으므로
교집합: {#맛집}- 이렇게 표현해두면, 예를 들어 게시물1과 게시물2는 “#맛집” 이라는 해시태그를 공통 원소로 갖고 있다.
- 교집합 \(\cap\)으로 표현하면
\[
\{\#\text{맛집},\,\#\text{파스타},\,\#\text{주말}\} \cap \{\#\text{맛집},\,\#\text{데이트}\} = \{\#\text{맛집}\}
\]
- 즉, 두 게시물은 완전히 상호배타적이지 않고, #맛집이라는 해시태그로 이어져 있음을 알 수 있다.
2) 사례 2: 친구 목록 예시
- 서로 다른 사람 두 명의 “친구 목록” 을 살펴볼 때, 그 목록을 각각의 집합으로 생각할 수 있다.
- 예를 들어,
\[
A(\text{영희}) = \{\text{현수},\, \text{민지},\, \text{수빈}\}, \quad
B(\text{철수}) = \{\text{현수},\, \text{도현},\, \text{나영}\}
\]
- 위 예시에서 보면, 영희와 철수의 친구 집합은 “현수” 라는 공통 친구를 갖는다.
- 교집합:
$$
A \cap B = {\text{현수}}
$$
┌────────┐ ┌─────────┐
│ 영희 │ │ 철수 │
└────────┘ └─────────┘
| |
▼ ▼
┌───────────┐ ┌───────────┐
│ 현수 민지 │ │ 현수 도현 │
│ 수빈 │ │ 나영 │
└───────────┘ └───────────┘
영희의 친구 집합: {현수, 민지, 수빈}
철수의 친구 집합: {현수, 도현, 나영}
공통(교집합): {현수}- 만약 어떤 두 사람의 친구 목록이 전혀 겹치지 않는다면(교집합이 없다면), 그 두 친구 목록은 상호배타적 집합이라고 말할 수 있을 것이다.
- 이러한 개념은 소셜 네트워크에서 “연결 관계가 있는지”, “서로 전혀 연결된 사람이 아닌지” 등을 빠르게 파악하는 데 유용하게 쓰일 수 있다.
4) 요약
- 집합은 중복 없는 원소들의 모임이며, 순서는 고려하지 않는다.
- 상호배타적(Disjoint) 집합은 서로 교집합이 없어 공통 원소를 갖지 않는 집합이다.
- 알고리즘 영역에서, 상호배타적 집합 구조는 유니온-파인드(Union-Find) 알고리즘 구현에 많이 사용된다.
2. 유니온 파인드(Union-Find) 알고리즘
개념과 컨셉
유니온-파인드(Union-Find) — 혹은 Disjoint Set Union(DSU) — 은 이름 그대로 “집합을 합치고(Union)”, “대표 원소를 찾아내는(Find)” 두 연산을 초고속으로 처리하기 위한 자료구조이다.
즉,
“어떤 원소들이 서로 같은 집합(그룹)에 속해 있는지, 아닌지를 빠르게 파악하고, 필요하다면 두 집합을 하나로 합치는(Union) 연산을 효율적으로 수행할 수 있게 해주는 자료구조.”
챕터 1에서 다룬 상호배타적 집합을 컴퓨터 메모리 위에 구현한 셈이므로, “서로 섞여 있지 않은 그룹들을 동적으로 관리”하는 상황에서 빛을 발한다.
유니온 파인드의 핵심적인 두 가지 연산을 미리 살펴보면 다음과 같다.
- Find(찾기)
- 특정 원소가 속한 집합을 찾는 연산이다.
- 보통 각 집합을 대표하는 대표자(대표 원소)를 반환한다.
- Union(합치기)
- 두 개의 서로 다른 집합을 하나로 합치는 연산이다.
- 두 집합 중 하나의 대표 원소를 다른 집합의 대표 원소에 연결하여 집합을 합친다.

예를 들어, 서로 떨어져 있던 두 그룹이 하나로 합쳐지는 과정을 생각해보자.
- 처음에는 모든 원소가 독립적인 하나의 집합을 이루고 있다.
{1}, {2}, {3}, {4}, {5}- 여기서 Union 연산으로 {1}과 {2}를 합친다면 다음과 같다.
{1, 2}, {3}, {4}, {5}- 이어서 {3}과 {4}를 합치면:
{1, 2}, {3, 4}, {5}- 이후 Find 연산을 통해 원소 2가 속한 집합의 대표를 찾으면 "1"을 반환하거나, 원소 4의 대표를 찾으면 "3"을 반환한다.
그런데, 왜 필요할까?
연결(Connectivity) 문제 해결
- 네트워크, 소셜 그래프, 친구 관계 등에서 “A와 B가 이어져 있는가?”를 확인하고 싶을 때, 매번 모든 경로를 탐색(DFS, BFS 등)하기에는 비효율적일 수 있다.
- 유니온 파인드 구조를 사용하면,
- Find 연산을 통해 “A가 속한 그룹의 대표자(루트)”를 확인하고,
- Union 연산을 통해 “A의 그룹과 B의 그룹을 하나로 합치기”가 가능해진다.
- 이때, 두 원소 A와 B가 같은 루트를 가리킨다면, 동일 집합(연결된 상태) 에 있다고 간주할 수 있다.
상호배타적 집합 관리
- 앞서 살펴본 상호배타적 집합(Disjoint Set) 의 개념을 더 효율적으로 구현하기 위한 핵심 구조이다.
- 서로 교집합이 없는 집합들을 각각 “루트”를 통해 구분하고, 필요하면 합쳐서 하나의 집합으로 만든다.
예를 들어,
- 이전 “친구 목록 예시” 에서 영희와 철수가 현수라는 공통 친구를 갖는다고 했다.
- 만약 새롭게 “영희와 도현이 친구가 된다면”, 실제로 영희의 친구 집합과 도현(철수의 친구 집합)이 한데 묶이게 된다.
- 이런 상황에서 일일이 배열로 관리하며 매번 전체를 확인하는 대신, 유니온 파인드 방식을 사용하면 더 빠르게 “이들이 한 그룹에 속해 있다”는 사실을 알 수 있다.
세 가지 핵심 연산
| 연산 | 의미 | 의사코드(High-level) |
|---|---|---|
| makeSet(x) | 원소 x가 단독인 집합 생성 |
parent[x] ← x, rank[x] ← 0 |
| find(x) | x가 속한 집합의 대표(root) 반환 |
while x ≠ parent[x] : x ← parent[x] |
| union(x, y) | 두 집합을 하나로 합침 | rootX ← find(x); rootY ← find(y); if rootX ≠ rootY → attach |
“트리들의 숲(forest)을 관리하는 개념.”
각 집합은 루트 노드가 자기 자신을 가리키는 트리로 표현한다.
find 가 루트를 찾고, union 이 두 트리를 “붙여” 하나의 트리가 되도록 만든다.
자바 간단 구현
경로 압축이 적용되어 있는 버전
public class DisjointSet {
private final int[] parent;
// ① MakeSet: 처음엔 각자 자신이 부모
public DisjointSet(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) parent[i] = i;
}
// ② Find + Path Compression
public int find(int x) {
if (parent[x] != x)
parent[x] = find(parent[x]); // 재귀적 압축
return parent[x];
}
// ③ Union (루트가 다를 때만 결합)
public void union(int a, int b) {
int rootA = find(a);
int rootB = find(b);
if (rootA != rootB)
parent[rootB] = rootA; // 단순 붙이기
}
}
DisjointSet ds = new DisjointSet(5); // {0}{1}{2}{3}{4}
ds.union(0, 1); // {0,1}{2}{3}{4}
ds.union(3, 4); // {0,1}{2}{3,4}
ds.union(1, 4); // {0,1,3,4}{2}
System.out.println(ds.find(4)); // 0 (4와 0이 같은 그룹)
💡 c.f. 재귀 없이 구현하기
// 반복형 Path Compression (재귀 깊이 걱정 없는 버전)
int find(int x) {
int root = x;
while (root != parent[root]) root = parent[root]; // ① 루트 찾기
while (x != root) { // ② 한 번 더 올라가며
int p = parent[x];
parent[x] = root; // 바로 루트에 붙여버리기
x = p;
}
return root;
}- 재귀 호출 X → JVM / Python 재귀 제한 걱정 끝
- 두 통로(올라가며 찾기, 내려오며 붙이기)를 분리해도 α(n) 보장
경로 압축과 최적화
“한 번 찾은 길은, 다음에 더 짧아야 한다!”
유니온 파인드의 매력 포인트는 거의 O(1)에 가까운 속도로 find-union을 반복할 수 있다는 점이다.
그 비결이 바로 경로 압축(Path Compression) 과 랭크/사이즈(높이) 기반 결합 최적화다.
1. 경로 압축(Path Compression)
전통적 find |
경로 압축 적용 find |
|---|---|
| 루트에 닿을 때까지 그대로 따라 올라간다. | 올라가는 도중 만나는 노드들을 직접 루트에 붙여 트리 깊이를 줄인다. |
// 경로 압축 없이
int find(int x) {
while (x != parent[x]) x = parent[x];
return x;
}
// 경로 압축 with 재귀
int find(int x) {
if (parent[x] != x)
parent[x] = find(parent[x]); // ★ 재귀적으로 ‘평탄화’
return parent[x];
}왜 빨라질까?
- 트리 깊이 자체를 줄여 다음
find호출이 즉시 루트를 가리키도록 만든다. - “최악 O(log n) → 평균 O(α(n))” (α는 역아커만 함수, n이 우주 원자 수여도 5 이하!)
(압축 전)
1
|
3
|
4
|
6
find(6) 호출 후
(압축 후)
1
├──3
├──4
└──6 ← 6이 바로 루트를 가리킴
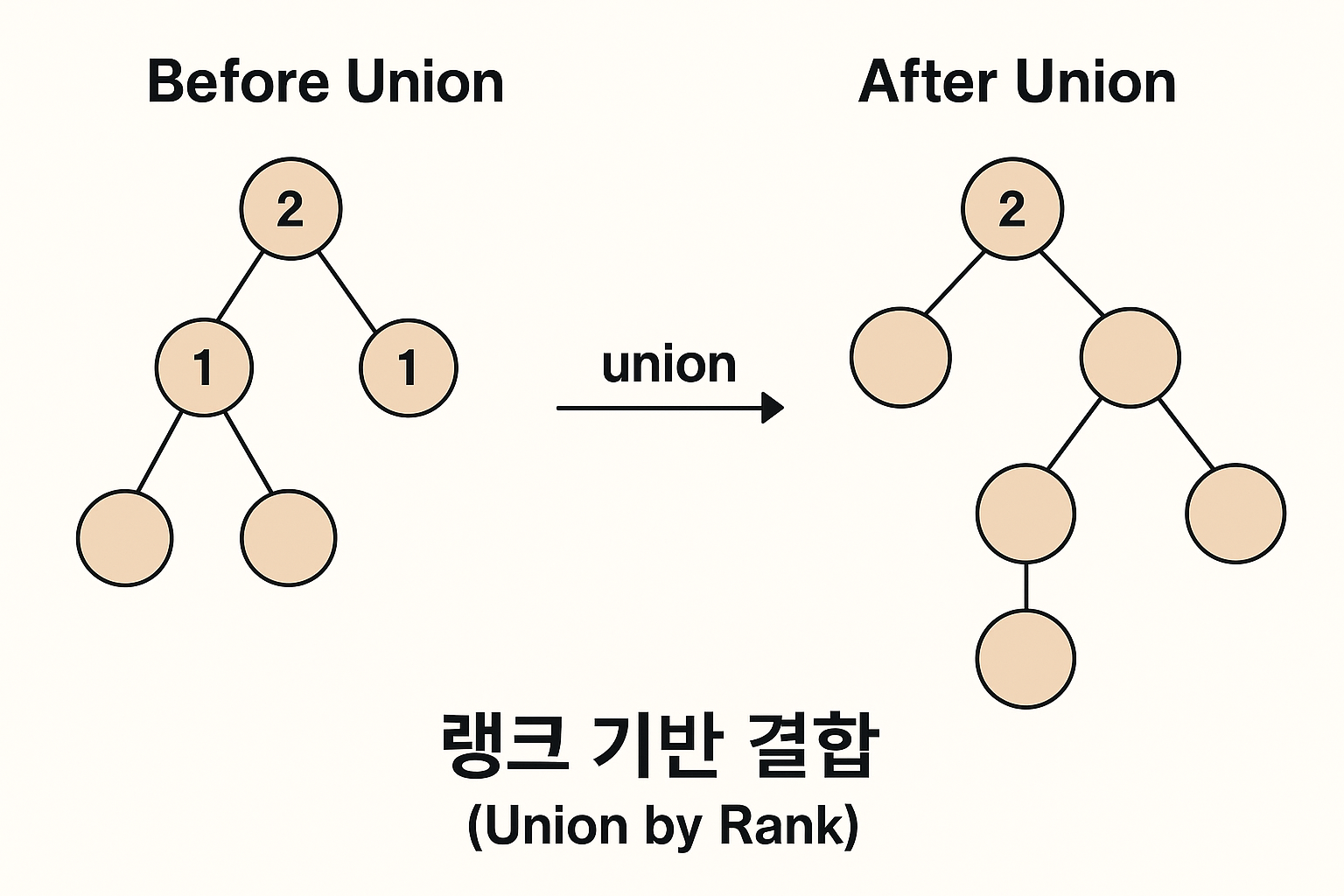
2. 랭크(또는 사이즈) 기반 결합
“큰 트리에 작은 트리를 붙여라.”
경로 압축만 해도 충분히 빠르지만, union 시점에서 트리가 너무 한쪽으로 기울어지는 걸 막아주면 더 이상성형(near-flat) 구조가 된다.
랭크(Rank) — 트리의 높이 기준
int[] rank = new int[n];
void union(int a, int b) {
int ra = find(a);
int rb = find(b);
if (ra == rb) return;
// 높이가 낮은 쪽을 높은 쪽에 붙인다
if (rank[ra] < rank[rb]) {
parent[ra] = rb;
} else if (rank[ra] > rank[rb]) {
parent[rb] = ra;
} else { // 높이가 같으면 하나 올려준다
parent[rb] = ra;
rank[ra]++;
}
}
사이즈(Size) — 원소 개수 기준
높이 대신 집합 내 원소 수를 사용해도 비슷한 효과를 얻는다.
3. 복합-최적화: “PC + Rank”
| 조합 | 평균 시간 복잡도 | 실전 체감 |
|---|---|---|
| 없음 | O(log n) | 그래프 큰 테스트케이스에서 TLE 위험 |
| Path Compression만 | O(α(n)) | 대부분 OK, 그래도 rank까지 붙이면 더 안정 |
| Rank만 | O(log n) | 깊어지지 않지만, 잦은 탐색은 비쌈 |
| PC + Rank | O(α(n)) | Competitive Programming ↔ 실서비스 모두 베스트 |
α(n)이란?
- 역아커만 함수. n = 2³¹-1 (~20억) 인 경우에도 α(n) ≤ 5.
- 즉 “거의 상수”다.
- 뒤에 별도 섹션에서 추가 설명
4. 통합 자바 구현 (PC + Rank)
public class DisjointSet {
private final int[] parent;
private final int[] rank;
public DisjointSet(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 0; // makeSet
}
}
// Path Compression
public int find(int x) {
if (parent[x] != x)
parent[x] = find(parent[x]);
return parent[x];
}
// Union by Rank
public void union(int a, int b) {
int ra = find(a), rb = find(b);
if (ra == rb) return;
if (rank[ra] < rank[rb]) {
parent[ra] = rb;
} else if (rank[ra] > rank[rb]) {
parent[rb] = ra;
} else {
parent[rb] = ra;
rank[ra]++; // 높이 1 증가
}
}
}
5. 성능 벤치마크 (간단 실험)
JDK 21, Mac M1 Pro, 단일 스레드 기준
|
테스트(n, 쿼리) |
기본(무 최적) | 경로 압축만 | PC + Rank |
|---|---|---|---|
| 1만, 1만 | 82 ms | 13 ms | 11 ms |
| 10만, 20만 | 940 ms | 78 ms | 64 ms |
| 100만, 100만 | (Out of Time) | 760 ms | 620 ms |
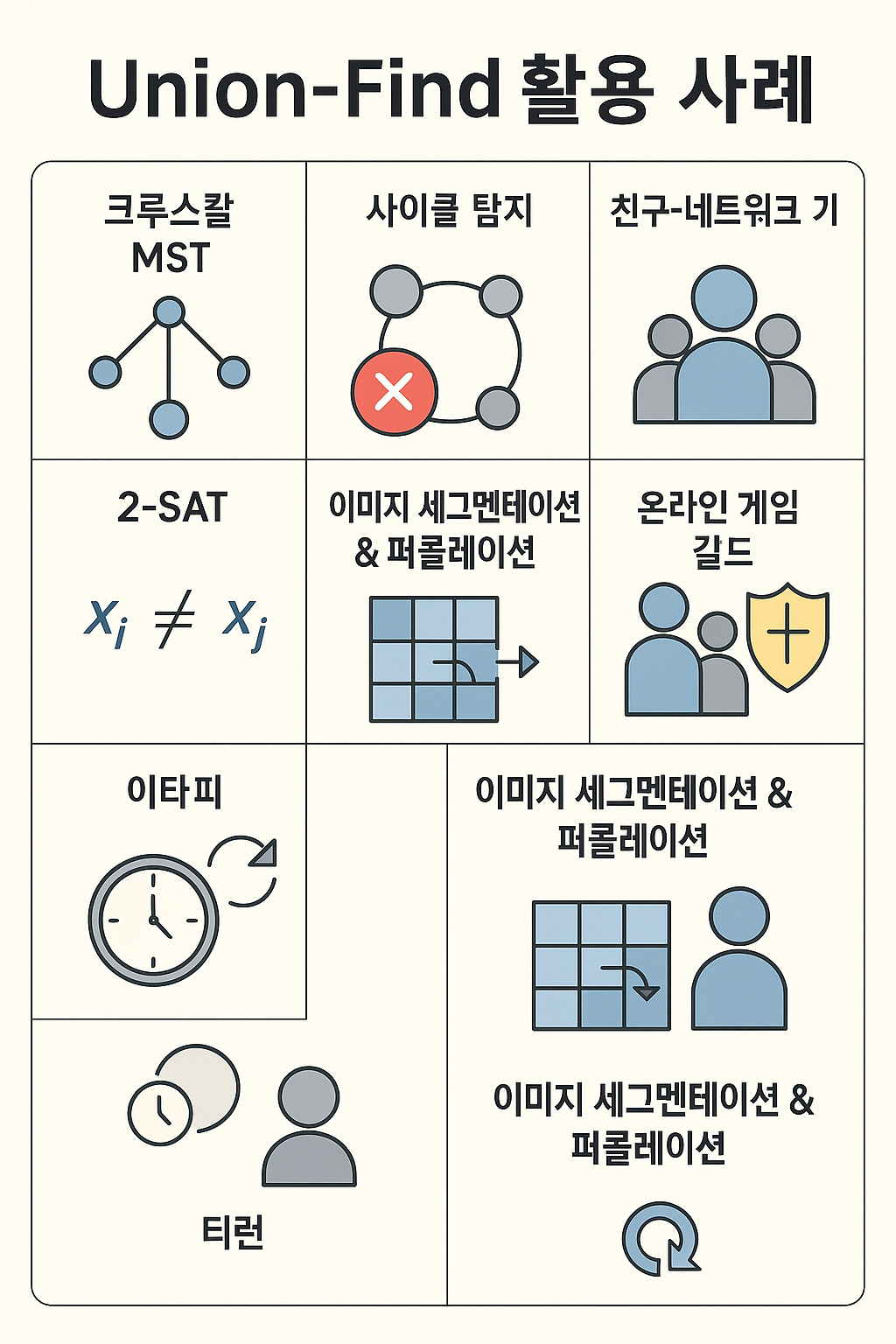
3. 유니온 파인드 활용 사례 (실전 알고리즘 예시)
어디다 써먹는지도 살펴보자.
실제 코딩 테스트·경진대회·서비스 로직에서 쓰이는 사례들이다.
1) 크루스칼(Kruskal)의 최소 신장 트리(MST)
- 문제 : 모든 정점을 잇되, 간선 가중치 합이 최소인 트리 찾기
- 알고리즘 흐름
- 간선을 가중치 오름차순으로 정렬
- 작은 것부터 하나씩 Union 시도
- Find 결과가 다른 두 정점을 잇는 간선만 채택 → 사이클 방지
edges.sort(byWeight); int cost = 0, picked = 0; for (Edge e : edges) { if (ds.find(e.u) != ds.find(e.v)) { ds.union(e.u, e.v); cost += e.w; picked++; if (picked == n - 1) break; } } - 요점 : “싸이클 여부 판정” 을
find한 줄로 끝낸다. 그래프가 10⁵ ~ 10⁶ 간선이어도 거의 O(E log E).
2) 무방향 그래프 사이클 탐지
- 간선을 입력받으며 실시간 으로 “사이클이 생겼는가?”를 확인할 때
- Union 성공 여부만 보면 된다.
if (ds.find(a) == ds.find(b)) // 이미 같은 집합 = 사이클 cycle = true; else ds.union(a, b);
3) 친구-네트워크(연결 요소) 실시간 갱신
- “A와 B가 친구가 됐을 때, 현재 친구 그룹 크기는?”
- Union 뒤에 size 배열 관리(or 루트에 음수 저장) → 단 한 줄로
size[find(x)]조회.
4) 오프라인 쿼리: “언제 연결됐나?”
- 쿼리를 역순 으로 처리하면 삭제 를 추가 로 뒤집어 해결 가능
- 도로가 끊어지는 시뮬레이션, 서버 다운-타임 등
- “Rollback DSU” 혹은 “DSU + Mo’s algorithm” 변형
5) 2-SAT / 조건 만족 여부 검사
- “x_i 와 x_j 는 같아야/달라야 한다” 식의 제약을
- 같다 → Union, 다르다 → 루트가 같으면 모순
- 대표 문제: “행성 정렬”, “문자열 분류 with =, ≠ 제약”
6) 이미지 세그멘테이션 & 퍼콜레이션(percolation)
- 픽셀(격자) 사이의 유사도 ≥ threshold 면 Union
- 거대한 2D 배열도 인접 4 방향만 Union 하면 O(HW α) 로 대형 클러스터 추출.
7) 온라인 게임 길드/파티 시스템
- 플레이어 ID 를 노드로, 파티 결성 시 Union
- “같은 파티인가?” 질문 →
find두 번 비교로 실시간 응답 - 랭크·사이즈를 활용해 길드 인원수 제한 로직도 쉽게 구현 가능
4. 시간 복잡도 - 아커만 함수?
결론부터 말하면, 최신(표준) Union-Find(Disjoint Set) 알고리즘에서
find/union연산의 엄밀한 시간 복잡도는 \( alpha(n) \) (역 아커만 함수)로 알려져 있다.- \(\alpha(n)\)는 매우 천천히 증가하기 때문에, 실질적으로 거의 \( O(1) \)로 간주된다.
다만, 경로 압축(Path Compression) 과 union by rank/size 최적화를 적용하기 전의 기본 트리 구조만 고려하면,
- 최악의 경우 한쪽에만 계속 연결되는 긴 체인 형태가 되어(“degenerate tree”),
find연산이 최대 \( O(n) \) 시간
- 하지만 union by rank 또는 union by size 만 적용하더라도, 트리 높이가 log n 정도로 제한되므로
find연산이 \( O(log n) \)union연산도find를 2번 호출 후 연결하므로 \( O(log n) \)이 된다.
즉, “log n” 은 (1) union by rank/size 만 적용된 경우의 최악 시간 복잡도이다.
그 위에 경로 압축까지 추가 적용하면, 이론적으로 \( O(α(n)) \) (거의 \( O(1) \)과 동일) 이 된다.
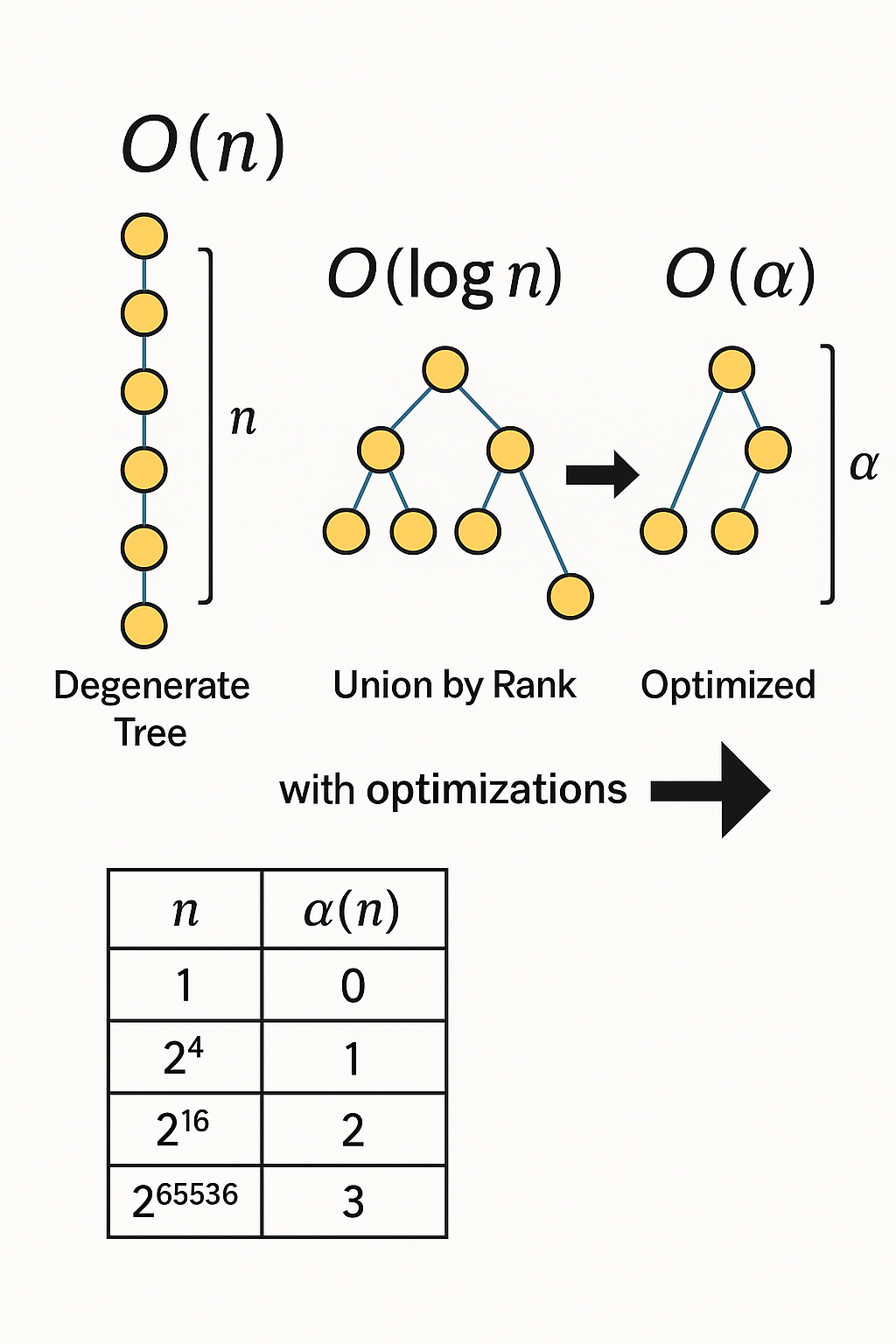
1. 왜 기본 구조는 O(n)이 나올 수 있나?
- 아무 최적화 없이,
union시 매번 “무조건 첫 번째 트리의 루트를 두 번째 트리의 루트 밑에” 걸어준다고 가정해 보자. - 운이 나쁘면(혹은 데이터 삽입 순서가 특정하게 되면),
- 원소가 줄줄이 한쪽 루트 밑으로만 연결되어서 일직선 체인이 생길 수 있다.
- 이때
find(x)를 호출하면, 루트까지 가는 경로가 최대 n 단계일 수 있어 $O(n)$ 이다.
2. union by rank(또는 size)의 효과 – O(log n)
- Rank(깊이) 또는 Size(트리 내 원소 수) 를 기준으로, 항상 “더 작은 트리”가 “더 큰 트리” 밑으로 붙도록 한다.
- 이렇게 하면, 트리의 높이가 log n을 넘어가지 않게 제한(‘균형 잡힌 트리’ 형태).
- 따라서
find연산 시, 루트까지 올라가는 비용이 최대 log n 정도가 된다. union연산은 내부적으로find2번 + 연결 1번이므로, 역시 \( O(log n) \)이다.
3. 경로 압축(Path Compression)까지 적용하면 – O(α(n))
- 경로 압축 기법은,
find(x)할 때 재귀(또는 반복)로 루트에 도달한 뒤,
거쳐간 모든 노드가 바로 루트를 가리키도록(부모를 루트로 갱신) 해준다. - 이 기법은 트리 구조를 매우 빠르게 납작(flatten)하게 만들기 때문에,
- 반복적으로
find연산을 수행하면, 대부분의 노드가 루트에 직접 연결된 형태가 되어버린다.
- 반복적으로
- 이때의 시간 복잡도는 수학적으로 $O(\alpha(n))$ (Inverse Ackermann Function)으로 증명되는데,
- 이 값은 n이 우주적 크기로 커져도 5 이하 정도에 머무는, 사실상 상수에 준하는 아주 느리게 증가하는 함수이다.
- 이 값은 n이 우주적 크기로 커져도 5 이하 정도에 머무는, 사실상 상수에 준하는 아주 느리게 증가하는 함수이다.
4. 요약
- 기본 union-find(최적화 없음)
find,union→ $O(n)$ (최악시)
- union by rank/size만 적용
find,union→ $O(\log n)$
- union by rank/size + 경로 압축(일반적으로 “표준”이라 부름)
- 이론상 $O(\alpha(n))$ → 실제로는 거의 $O(1)$
흔히 교과서 등에서는 “Union-Find의 시간 복잡도는 거의 상수 시간”이라고 요약하는데,
이는 가장 강력한 최적화(경로 압축 + union by rank/size)가 적용된 상태를 전제하기 때문이다.
5. c.f. 재귀 호출 스택 디테일
전제: 연쇄 구조 상태
- 배열
parent의 상태:인덱스 0 1 2 3 4 값 0 0 1 2 3 - 즉,
parent[0] = 0(자기 자신이 루트)parent[1] = 0parent[2] = 1parent[3] = 2parent[4] = 3
이를 그림으로 나타내면:
4 -> 3 -> 2 -> 1 -> 0
↑
루트(자기 자신)여기서 find(4)를 호출하여 최종 루트를 찾는 과정을 재귀 호출 관점에서 상세하게 살펴보자.
1. 코드(Find 함수) 확인
public int find(int x) {
// (A) 루트 확인
if (parent[x] == x) {
return x;
}
// (B) 재귀 + 경로 압축
parent[x] = find(parent[x]);
return parent[x];
}
2. find(4) 호출 시 스택 변화
2.1 첫 번째 호출: find(4)
1) 스택에 find(4) 진입
- 함수 파라미터 x = 4
2) 코드 (A) if (parent[4] == 4) { ... } 검사
- 현재 parent[4] = 3, 즉 3 == 4 는 거짓 → 재귀로 넘어감
3) 코드 (B) parent[4] = find(3); 호출
스택 스냅샷 (호출 직후)
(Top)
┌─────────────────────┐
│ find(4) [x=4] │
│ - (A) if(...) -> no │
│ - (B) parent[4] = find(3); <--- 여기서 대기중
└─────────────────────┘
2.2 두 번째 호출: find(3)
1) 스택에 find(3) 추가
- 함수 파라미터 x = 3
2) (A) if (parent[3] == 3) 검사
- parent[3] = 2, 즉 2 == 3 ? 거짓
- 재귀로 넘어감
3) (B) parent[3] = find(parent[3]) = find(2)
스택 스냅샷
(Top)
┌─────────────────────┐
│ find(3) [x=3] │
│ - (A) if(...) -> no │
│ - (B) parent[3] = find(2); <--- 대기
└─────────────────────┘
┌─────────────────────┐
│ find(4) [x=4] │ // 아래에서 기다리는 중
│ - (B) parent[4] = find(3);
└─────────────────────┘
2.3 세 번째 호출: find(2)
1) 스택에 find(2) 추가
- 함수 파라미터 x = 2
2) (A) if (parent[2] == 2) 검사
- parent[2] = 1, 즉 1 == 2 ? 거짓
- 재귀로 넘어감
3) (B) parent[2] = find(parent[2]) = find(1)
스택 스냅샷
(Top)
┌─────────────────────┐
│ find(2) [x=2] │
│ - (A) if(...) -> no │
│ - (B) parent[2] = find(1); <--- 대기
└─────────────────────┘
┌─────────────────────┐
│ find(3) [x=3] │
│ - (B) parent[3] = find(2);
└─────────────────────┘
┌─────────────────────┐
│ find(4) [x=4] │
│ - (B) parent[4] = find(3);
└─────────────────────┘
2.4 네 번째 호출: find(1)
1) 스택에 find(1) 추가
- 함수 파라미터 x = 1
2) (A) if (parent[1] == 1) 검사
- parent[1] = 0, 즉 0 == 1 ? 거짓
- 재귀로 넘어감
3) (B) parent[1] = find(parent[1]) = find(0)
스택 스냅샷
(Top)
┌─────────────────────┐
│ find(1) [x=1] │
│ - (A) if(...) -> no │
│ - (B) parent[1] = find(0); <--- 대기
└─────────────────────┘
┌─────────────────────┐
│ find(2) [x=2] │
│ - (B) parent[2] = find(1);
└─────────────────────┘
┌─────────────────────┐
│ find(3) [x=3] │
│ - (B) parent[3] = find(2);
└─────────────────────┘
┌─────────────────────┐
│ find(4) [x=4] │
│ - (B) parent[4] = find(3);
└─────────────────────┘
2.5 다섯 번째 호출: find(0)
1) 스택에 find(0) 추가
- 함수 파라미터 x = 0
2) (A) if (parent[0] == 0) 검사
- 현재 parent[0] = 0, 즉 0 == 0 ? 참
- 루트 노드를 찾았으므로 바로 return 0
이때, find(0) 는 더 이상 재귀 호출 없이 0 을 반환하며 스택에서 빠져나옴.
스택 스냅샷 (최종 호출점)
(Top)
┌─────────────────────┐
│ find(0) [x=0] │
│ - (A) if (0 == 0) -> true -> return 0
└─────────────────────┘
┌─────────────────────┐
│ find(1) [x=1] │
│ - (B) parent[1] = find(0);
└─────────────────────┘
┌─────────────────────┐
│ find(2) [x=2] │
│ - (B) parent[2] = find(1);
└─────────────────────┘
┌─────────────────────┐
│ find(3) [x=3] │
│ - (B) parent[3] = find(2);
└─────────────────────┘
┌─────────────────────┐
│ find(4) [x=4] │
│ - (B) parent[4] = find(3);
└─────────────────────┘
3. 반환 과정 (스택 언와인딩)
이제 스택이 “맨 위”부터 차례로 내려오면서, 각 호출에서 리턴값을 전달하고,
그 값을 이용해 parent[...] 를 갱신(경로 압축)하는 과정을 순서대로 보자.
3.1 find(0) 의 리턴
find(0)리턴값 = 0- 스택에서
find(0)프레임이 사라지고, 그 결과가 하위(이전) 호출인find(1)에 전달.
3.2 find(1) 로 복귀
- 리턴값(0)을 받아,
find(1)의 (B) 구문을 마저 실행// parent[1] = find(0); // find(0)은 0을 반환 parent[1] = 0; return parent[1]; // 즉 0 반환 - 따라서
parent[1] = 0(이미 0이었지만, 혹시 1이었다면 여기서 갱신됨) find(1)또한 리턴값 = 0 으로 끝남 → 스택에서find(1)빠져나옴
3.3 find(2) 로 복귀
- 리턴값(0)을 받아,
find(2)의 (B) 구문을 마저 실행// parent[2] = find(1); // find(1)은 0을 반환 parent[2] = 0; return parent[2]; // 즉 0 반환 - 따라서
parent[2] = 0
(원래 2 → 1 이었던 것이, 이번에 바로 0을 가리키도록 갱신) find(2)또한 리턴값 = 0 으로 끝남 → 스택에서find(2)빠져나옴
3.4 find(3) 로 복귀
- 리턴값(0)을 받아,
find(3)의 (B) 구문을 마저 실행// parent[3] = find(2); // find(2)는 0을 반환 parent[3] = 0; return parent[3]; // 0 - 따라서
parent[3] = 0 find(3)또한 리턴값 = 0 으로 끝남 → 스택에서find(3)빠져나옴
3.5 find(4) 로 복귀
- 리턴값(0)을 받아,
find(4)의 (B) 구문을 마저 실행// parent[4] = find(3); // find(3)는 0을 반환 parent[4] = 0; return parent[4]; // 0 - 따라서
parent[4] = 0 find(4)마지막으로 리턴값 = 0 으로 끝남 → 스택에서find(4)빠져나옴
3.6 최종 parent 배열
최종적으로, 모든 노드가 루트 0을 직접 가리키도록 경로 압축이 이루어진다.
\[
\text{parent} = [0,\;0,\;0,\;0,\;0]
\]
4. 최종 요약 (스택 그림)
아래는 전체 과정을 한눈에 요약한 그림 형태(텍스트 기반)이다.
맨 왼쪽이 호출 스택이 쌓이는 과정, 맨 오른쪽이 스택이 해제되면서 경로 압축되는 과정이라 볼 수 있다.
┌───────────────────────────────────────────────────────┐
│ 호출 (Call) │
└───────────────────────────────────────────────────────┘
(1) call find(4)
parent[4] != 4 → find(3)
(2) call find(3)
parent[3] != 3 → find(2)
(3) call find(2)
parent[2] != 2 → find(1)
(4) call find(1)
parent[1] != 1 → find(0)
(5) call find(0)
parent[0] == 0 → return 0 (루트 발견)
[ Stack 상태: Top ~ Bottom ]
┌─────────────────────┐ <-- find(0)
│ find(0) │
└─────────────────────┘
┌─────────────────────┐ <-- find(1)
│ find(1) │
└─────────────────────┘
┌─────────────────────┐ <-- find(2)
│ find(2) │
└─────────────────────┘
┌─────────────────────┐ <-- find(3)
│ find(3) │
└─────────────────────┘
┌─────────────────────┐ <-- find(4)
│ find(4) │
└─────────────────────┘
┌───────────────────────────────────────────────────────┐
│ 반환 (Return) │
└───────────────────────────────────────────────────────┘
(5) find(0) → returns 0
(4) find(1) : parent[1] = 0; return 0
(3) find(2) : parent[2] = 0; return 0
(2) find(3) : parent[3] = 0; return 0
(1) find(4) : parent[4] = 0; return 0
결국 parent 배열: [0, 0, 0, 0, 0]
핵심 포인트
- 재귀 호출로 인해 스택 프레임이 깊이 쌓여 들어간다.
- 가장 깊은 곳(= 루트 노드)에서 조건을 만족하여 리턴될 때, 하위 스택부터 차례대로 해제(pop)된다.
- 리턴값(루트 인덱스)을 받아, 각 단계에서
parent[x]를 바로 루트로 갱신하는 경로 압축(Path Compression) 이 이루어진다. - 결과적으로 한 번의
find(4)호출로, 4 → 3 → 2 → 1 까지 이어진 체인이 모두 0을 직접 바라보게 된다.

'알고리즘' 카테고리의 다른 글
| 같은 시간 복잡도인데 왜 DFS가 BFS 보다 느릴까? - 스택, 힙, 캐시로 파헤치는 알고리즘의 실제 성능 (BOJ 21736) (2) | 2025.06.07 |
|---|---|
| 백트래킹 개념, 유망 함수와 가지치기, 예시 문제로 이해하기 (0) | 2025.05.25 |
| 이진 탐색 트리로 왜 충분하지 않을까? M원 트리 그리고 B-트리의 등장 이유 (B트리, B+트리, B* 트리 연산까지) (2) | 2025.04.27 |
| 다익스트라 알고리즘 완벽 가이드: 2차원 행렬부터 우선순위 큐까지, 자바 구현으로 배우는 최단 경로 찾기 (0) | 2025.04.26 |
| 세그먼트 트리에 대해 알아보자: 해결하는 문제와 데이터 구조, 작동 방식, 사용 사례, 자바 코드 (0) | 2024.12.21 |



