공개키 암호: 개념, 소인수분해 문제, 이산대수 문제, 타원곡선 문제, RSA, ElGamal 알고리즘

1. 공개기 암호의 개념

공개키 암호는 암호화와 복호화에 두 개의 서로 다른 공개키와 개인키를 사용하는 암호 방식이다.

C = Ek(P)
P = Dk(C)

이때 E는 암호화 함수, D는 복호화 함수를 의미한다.

공개키와 개인키는 언제나 한쌍으로 존재한다.

공개키는 누구나 이용할 수 있도록 공개하고 개인키는 자신만 이용하도록 공개하지 않는다. 만약 A가 B에게 보낼 메시지를 암호화하려면 B의 공개키를 이용하는 것이고, 이 암호문을 받은 B는 자신의 개인키를 이용하여 복호화한다.

공개키 암호는 비대칭키라고도 한다.

2. 기반 문제

어떻게 키를 공개했는데도 암호화 메커니즘이 동작하는지 의문이 들 수 있다. 핵심은 공개키 암호 알고리즘이 수학적으로 어려운 문제들에 기반을 두고 있다는 것이다.

어려운 문제라는 것은 무엇일까?

수학적으로 어려운 문제란, 한쪽 방향으로는 계산이 쉽지만, 반대쪽 방향으로는 계산이 어려운 문제를 의미한다.

즉, 함수 $f$가 주어질 때 $f(a)$를 계산해서 그 결과로 $b$를 얻는 것은 쉽지만, 함수 $f$의 역함수 $f^{-1}$에 대해 $f^{-1}(b)$를 계산해서 그 결과로 $a$를 얻는 것은 어려운 경우이다. 이 함수 $f$를 일방향 함수라고 한다.

계산이 쉽다는 것은 엄밀한 정의보다는 컴퓨터를 이용할 때 시간이 짧게 걸린다는 것을 의미한다.

다양한 일방향 함수가 존재한다. 소인수분해문제, 이산대수 문제, 타원곡선 이산대수 문제를 살펴보자.

1) 소인수분해 문제

소인수분해 문제는 어떤 두 정수의 곱은 빠른 시간에 구할 수 있지만, 임의의 양의 정수의 소인수분해는 매우 어렵다는 것이다.

예시: 곱셈과 소인수분해의 비교

다음과 같은 두 함수를 고려해 보자:

• $f_{MUL}(x, y) = xy$: 이 함수는 두 정수 $x$와 $y$를 입력받아 그들의 곱을 반환한다.
• $f_{FACT}(z) = {x, y | z = xy, x \neq 1, y \neq 1}$: 이 함수는 정수 $z$를 입력받아 그 소인수분해를 수행하고 소인수를 반환한다.

예시 설명

예를 들어, 정수 9539와 8887을 고려하면, 이들의 곱은 $f_{MUL}(9539, 8887) = 84,773,093$으로 계산이 매우 쉽다. 이러한 계산은 기본적인 곱셈 연산으로 빠르게 처리될 수 있다. 그러나 이 결과인 84,773,093을 소인수분해하는 것은 훨씬 복잡한 작업이다. $f_{FACT}(84,773,093)$를 실행하면 결과적으로 9539와 8887이라는 원래의 인수를 찾아내야 하는데, 이는 자원이 많이 드는 계산이다.

예를 들어, 256비트 크기의 숫자를 곱셈으로 처리할 때는 간단하지만, 소인수분해할 경우 약 8,000 MIPS-Year의 계산량이 필요하다.

암호학에서의 안전성을 보장하기 위해, 현재는 2,048비트 크기의 긴 키를 사용하는 것이 권장된다.

소인수분해 문제에 기반을 둔 공개키 알고리즘으로는 RSA가 대표적이다.

2) 이산대수 문제

이산대수 문제는 양의 정수 $n$, $a$, $x$에 대하여, $a^x \mod n$ 은 빠른 시간에 구할 수 있지만, 양의 정수 $n$, $a$, $y$에 대하여 $y = a^x \mod n$인 $x$를 구하는 것은 매우 어렵다는 것이다.

예를 들어, $n = 11$, $a = 2$, $x = 6$인 경우를 고려해보자. 이 경우 $2^6 \mod 11$을 계산하는 과정은 다음과 같다.

1. $2^2 \mod 11 = 4$
2. $4^2 \mod 11 = 16 \mod 11 = 5$
3. $5 \cdot 2 \mod 11 = 10 \mod 11 = 10$

따라서, $2^6 \mod 11 = 10$을 매우 빠르고 쉽게 계산할 수 있다. 하지만, 만약 $y = 10$이 주어졌고, $y = 2^x \mod 11$ 형태로 $x$를 찾아야 한다면, 이는 매우 어려운 작업이 된다. 주어진 $y$ 값에 대해 가능한 모든 $x$ 값을 시도해보며 $2^x \mod 11$이 $10$이 되는 지점을 찾아야 하기 때문이다.

이산대수 문제의 복잡성은 무작위로 $x$ 값을 시도하는 외에는 효율적으로 $x$를 찾을 수 있는 알고리즘이 현재까지 알려지지 않았기 때문에 매우 높다.

이산대수 문제는 여러 공개키 암호 알고리즘에서 사용되는데 대표적으로 ElGamal 암호, 디지털 서명 알고리즘(DSA) 및 그 변형인 KCDSA가 있으며, 디피-헬만 키 교환 프로토콜도 이 문제에 기반을 두고 있다.

3) 타원곡선 이산대수 문제

타원곡선 이산대수 문제는 일반적인 정수가 아닌 타원곡선상의 점과 타원곡선에서 정의되는 덧셈 연산을 이용하여 정의되는 이산대수 문제이다. 타원곡선
이산대수 문제 역시 이산대수 문제처럼 연산한 함수의 성질을 갖는다.

타원곡선 이산대수 문제에 기반을 둔 공개키 암호 알고리즘으로는 ECDSA, EC-KCDSA 등이 있다.

224비트 정도의 크기를 갖는 키를 사용하기를 권하고 있다.

3. 공개키 암호 알고리즘

RSA 알고리즘

RSA 암호 알고리즘은 1978년에 레퍼스트(Ron Rivest), 샤피르(AdiShamir), 애들먼(Leonard Adleman)에 의해 개발되어 현재 국제암호표준으로 활용되고 있다.

• 신용카드 결제, 증권거래, 이메일 등 많은 응용 분야에서 활용된다.
• 소인수분해 문제에 기반한다.
  -> 자릿수는 비슷하지만 두 수의 차가 큰 서로 다른 수 소수 p,q를 이용한다.

단계	행위자	내용
키 생성	수신자	공개키 (e,n)을 공개, 개인키 (d,p,q) 준비
암호화	송신자	n보다 작은 숫자인 평문 M을 수신자의 공개키 (e,n)을 이용하여 암호문 C 계산, C = M^e(mod n)
복호화	수신자	수신자의 개인키 (d,p,q)를 이용하여 암호문 C를 복호화, M = C^d(mod b)

먼저 키 생성 단계에서 수신자는 다음과 같은 작업을 통해 키를 생성한다. 이때 송신자가 누구인지는 몰라도 된다.

1. 두 개의 서로 다른 큰 소수 p와 q를 생성하여 n =pq를 계산한다.
2. 오일러의 함숫값ϕ(n)=(p−1)(q−1)과 서로소인 수 e를 임의로 선택한다.
3. ϕ(n)과 e로부터 확장 유클리드 알고리즘을 이용하여 ed≡1(mod ϕ(n)) 이 되는 d를 구한다.
4. e와 n을 공개키로 둔다.
5. d, p, q를 개인키로 둔다.

RSA 알고리즘의 핵심은 확장 유클리드 알고리즘을 활용하여 역원을 계산하는 것이다.

이 과정은 공개키의 일부인 $e$와 오일러의 피 함수 $\phi(n)$ 사이에서 $ed \equiv 1 \pmod{\phi(n)}$을 만족하는 $d$를 찾아내는 것이다. 이 $d$는 개인키의 중요한 부분이며, 공개키와 함께 사용되지 않기 때문에 매우 중요하다.

암호화 과정

암호화 과정에서는 송신자가 수신자의 공개키 $(e, n)$를 사용하여 평문 $M$을 암호문 $C$로 변환한다. 이 변환은 다음과 같은 수식을 통해 이루어진다.

$$
C = M^e \mod n
$$

복호화 과정

수신자는 자신의 개인키 $(d, p, q)$를 사용하여 암호문 $C$를 다시 평문 $M$으로 복호화한다. 복호화는 다음과 같은 공식을 사용한다.

$$
M = C^d \mod n
$$

복호화 과정은 송신자와 똑같은 방식으로 이루어지며, 송신자가 사용한 평문을 정확하게 복구한다.

소수 선택의 중요성

RSA에서 안전한 소수를 선택하는 것은 매우 중요하다. 이를 위해 다음과 같은 조건을 고려한다.

1. $p$와 $q$는 같은 자릿수여야 한다.
2. $p-1$과 $q-1$은 큰 소인수를 갖는다.
3. $GCD(p-1, q-1)$은 작은 값이어야 한다.
4. $|p-q|$는 충분히 커야 하며, 너무 가깝지 않아야 한다.

예시

1. 키 생성 (Bob):

• p, q 선택: 두 개의 서로 다른 큰 소수 ( p )와 ( q )를 선택

• n 계산: ( n = p \times q )를 계산 -> 이 숫자 ( n )은 공개키와 개인키 모두에 사용되는 모듈러스로 사용

• ( \phi(n) ) 계산: ( \phi(n) = (p-1) \times (q-1) )를 계산 -> 선택된 ( e )가 ( \phi(n) )과 서로소가 되도록 보장하는 데 사용

• e와 d 선택: ( 1 < e < \phi(n) ) 및 ( \text{gcd}(e, \phi(n)) = 1 ) 조건을 만족하는 암호화 키 ( e )를 선택. 복호화 키 ( d )는 ( e \times d \equiv 1 \mod \phi(n) )이 되도록 계산(확장 유클리드 알고리즘을 사용하여 ( e )의 ( \phi(n) ) 모듈로에 대한 곱셈 역원을 찾는다).

• 개인키는 ( (d, p, q) )로 구성되며 공개키는 ( (e, n) )

2. 암호화 (Alice에서 Bob으로):

• 공개키 (e, n): 앨리스는 밥의 공개키를 얻는다
• 암호화: 앨리스는 평문 ( P )를 ( C = P^e \mod n )로 계산하여 암호문 ( C )로 암호화

3. 복호화 (Bob):

• 개인키 (d, p, q): 밥은 복호화를 위해 자신의 개인키를 사용
• 복호화: 밥은 암호문 ( C )를 ( P = C^d \mod n )으로 계산하여 평문 ( P )를 복구

ElGamal 알고리즘

• 1985년 ElGamal이 제안
• 유한체상에서의 이산대수 문제이 기반
  -> 수신자의 공개키를 가지고 개인키를 계산하는 것은 이산대수 문제
• Diffie-Hellman 키 교환과 같은 원리를 이용

ElGamal 암호 알고리즘은 암호문의 길이가 평문 길이의 두 배로 늘어나고 계산량도 많기 때문에 RSA 보다 효율적이지 못한 단점이 있다.

예시

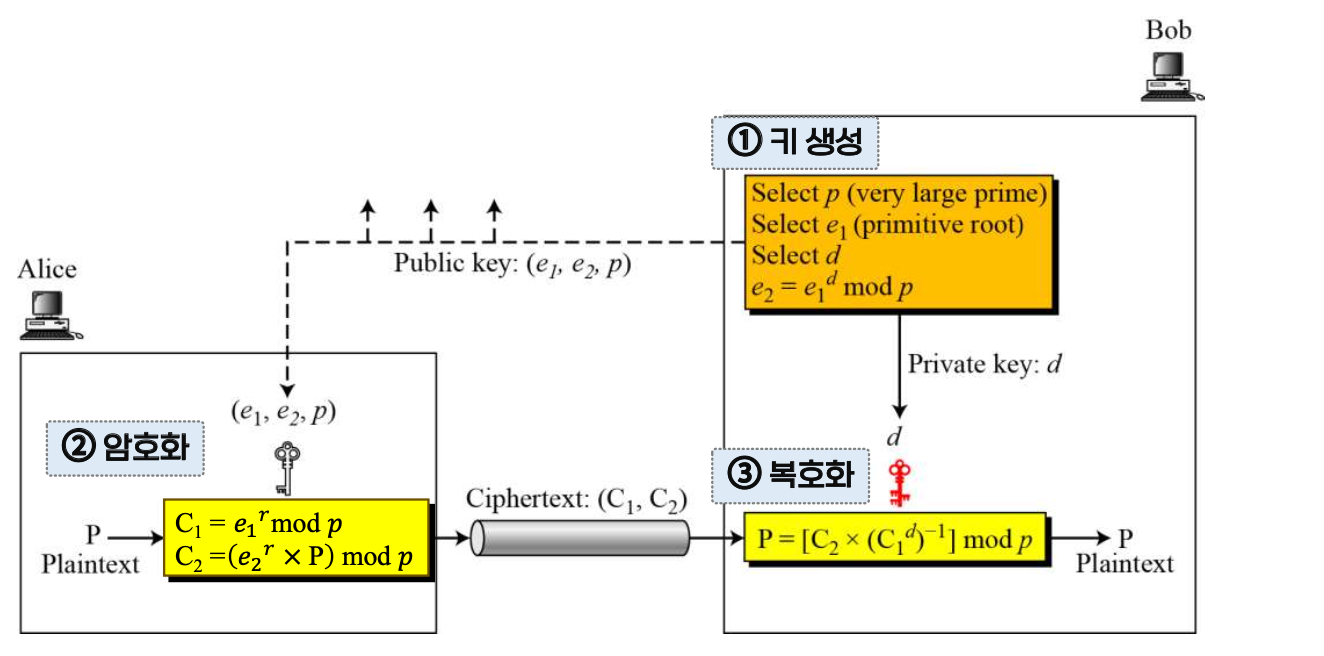
1. 키 생성 (Bob):

• p 선택: 매우 큰 소수 ( p )를 선택한다.
• ( e_1 ) 선택: ( p )에 대해 원시근 ( e_1 )을 선택한다.
• d 선택: 개인 지수 ( d )를 선택한다.
• ( e_2 ) 계산: ( e_2 = e_1^d \mod p )를 계산한다. 이 계산은 ElGamal에서 공개키를 생성하는 것과 유사하며, ( e_2 )는 개인키 ( d )에서 파생된 공개 구성 요소가 된다.

공개키는 ( (e_1, e_2, p) )이며, 개인키는 ( d )이다.

2. 암호화 (Alice):

• 공개키 ( (e_1, e_2, p) ): 앨리스는 Bob의 공개키를 암호화에 사용한다.
• 랜덤 ( r ) 생성: 앨리스는 랜덤 정수 ( r )을 선택한다.
• ( C_1 ) 계산: ( C_1 = e_1^r \mod p )를 계산한다.
• ( C_2 ) 계산: ( C_2 = (e_2^r \times P) \mod p )를 계산한다. 여기서 ( P )는 평문이며, 이 단계에서는 평문과 랜덤 ( r )을 사용하여 생성된 일시적 공개키 ( e_2^r )을 결합한다.

암호문은 ( (C_1, C_2) )이다.

3. 복호화 (Bob):

• 개인키 ( d ): Bob은 복호화를 위해 자신의 개인키를 사용한다.
• 복호화: Bob은 ( P = (C_2 \times (C_1^d)^{-1}) \mod p )를 계산한다. 여기서 ( C_1^d )는 모듈러 지수법의 특성 덕분에 ( (e_1^r)^d = e_2^r )이 되므로 ( e_2^r )을 재구성한다. ( C_2 )에 ( e_2^r )의 모듈러 역수를 곱함으로써 밥은 ( e_2^r ) 항을 상쇄하여 평문 ( P )을 복구한다.

이 방식은 Diffie-Hellman 키 교환 원리를 활용한다.

타원곡선 알고리즘

• ECC: Elliptic Curve Cryptosystem
• 1985년 Miller와 Koblitz가 독립적으로 제안
• 유한체상에서 정의된 타원곡선 군에서의 이산대수 문제에 기반

타원곡선 암호 알고리즘의 장점은 RSA, ElGamal 등과 동일한 수준의 보안성을 제공하면서도 키의 길이는 짧다는 점이다.
-> 이산대수 문제에 기반을 둔 ElGamal 암호 알고리즘 등을 변환하여 타원 곡선 암호 알고리즘으로 적용

메커니즘

타원곡선 이산대수 문제는 타원곡선 E와 타원곡선상의 한 점 P, 양의정수 k에 대해 kP는 빠른 시간에 구할 수 있지만, 타원곡선 E와 타원곡선상의 두 점 R과 P에 대해 R=kP가 되는 k를 구하는 것은 매우 어렵다는 것이다.

실제 타원곡선 암호에서 사용하는 타원곡선은 실수상에서 정의된 타원곡선이 아니라 유한체상에서 정의된 타원곡선 군을 이용한다. 즉, 타원곡선이 연속된 점들로 곡선처럼 나타내어지는 것이 아니라 점의 좌표 (x1, y1)의 값이 유한체의 원소들로 표현되는 개별 점들의 모임으로 나타내어진다.

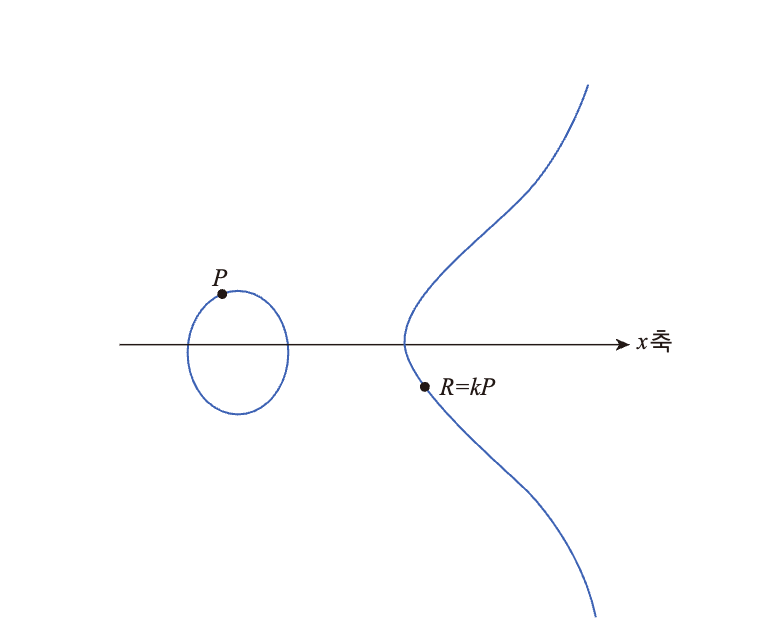
1. 스칼라 곱셈:

• ( P ): 타원 곡선 위의 한 점을 나타낸다.
• ( kP ): 정수 ( k )에 의한 점 ( P )의 스칼라 곱셈을 의미한다. 이는 점 ( P )를 ( k )번 자신에게 더하는 것과 같다.

2. 과정:

• 스칼라 곱셈은 반복된 덧셈과 유사하다. 만약 ( k = 3 )이라면, ( 3P = P + P + P )이다.
• 다이어그램은 특정 ( k )값에 대해 ( kP )를 보여주며, 이는 곡선 위의 점 ( R )을 결과로 나타낼 수 있다.

스칼라 곱셈은 안전한 키 교환을 위한 타원 곡선 디피-헬만(ECDH) 및 디지털 서명 생성과 검증을 위한 타원 곡선 디지털 서명 알고리즘(ECDSA)과 같은 알고리즘에서 사용된다.

여기서, 잘 선택된 매개변수에 대해 ( k )를 ( P )와 ( kP ) (타원 곡선 이산 로그 문제, ECDLP)로부터 계산하는 것이 계산적으로 불가능하기 때문에 ECC의 보안 기반이 된다.

---

참고자료: 컴퓨터보안(김진욱,유대현,김희천 공저 | 한국방송통신대학교출판문화원 | 2023)