컴퓨터와 데이터: 데이터와 정보, 진법 표현 - 정수, 실수, 문자

1. 데이터와 정보

1) 데이터와 정보의 관계

I = P(D)

데이터 D -> 처리기 P -> 정보 I

• 정보는 데이터를 처리하여 얻어지는 결과물
• 공식: I = P(D)
• 여기서 D는 데이터를, P는 처리 과정을, I는 정보를 의미.

데이터는 원재료 같은 것으로, 처리 과정을 거쳐 가공되고 변환되어 정보로 변화한다. 이렇게 생성된 정보는 특정 목적에 부합하는 결과를 제공하며, 이 과정을 우리는 '데이터 처리' 또는 '정보 처리'라고 한다.

2) 데이터의 표현 형태

데이터는 다양한 형태로 존재할 수 있다. 텍스트, 숫자, 이미지, 오디오, 비디오 등 다양한 유형이 있으며, 컴퓨터 내부에서는 이들을 모두 비트 패턴으로 표현한다.

 

메모리는 이러한 데이터를 저장하는 공간.

저장된 데이터의 유형을 구분하지 않고, 단순히 데이터 자체만을 저장한다.

 

이 데이터는 입출력 장치나 프로그램에 의해 해석되고 처리될 수 있다. 따라서, 같은 데이터라도 다른 방식으로 해석되어 다른 결과를 낼 수 있다.

3) 데이터의 표현 단위

컴퓨터에서 데이터를 표현하는 가장 기본적인 단위는 '비트' -> 비트는 이진수 체계를 따르며, 0과 1의 두 가지 상태만을 표현할 수 있다.

이들은 단순한 수치가 아니라 특정한 상태를 나타내는 기호로 사용된다.

 

또한, 여러 비트가 모여 '바이트'를 형성하며, 이 바이트들이 모여서 데이터의 더 큰 단위인 킬로바이트, 메가바이트, 기가바이트 등을 이룬다.

2. 진법

1) 진법

진법이란 숫자를 표현하는 방식으로, 어떤 진법을 사용하느냐에 따라 같은 수치도 다르게 표현될 수 있다.

 

우리가 일상에서 주로 사용하는 10진법은 0부터 9까지의 숫자를 사용하여 값을 표현.

컴퓨터는 0과 1, 두 가지 상태만을 이해하므로 2진법.

 

이 외에도 8진법과 16진법이 컴퓨터 과학에서 흔히 사용되는 진법이다.

2) 2진수 -> 10진수 변환

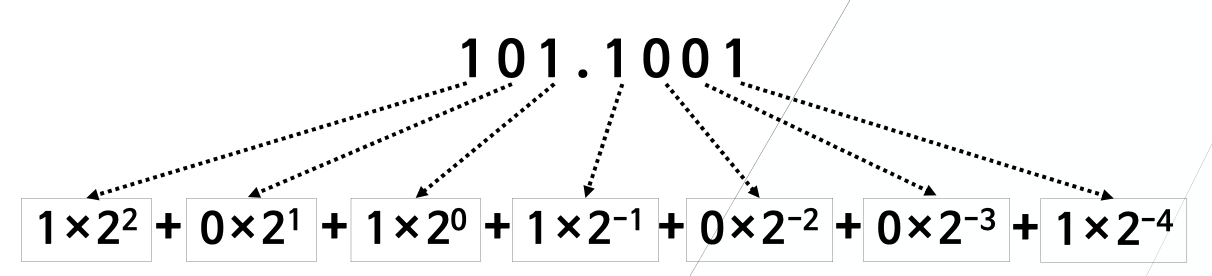
2진수를 10진수로 변환하는 것은 각 자릿수에 해당하는 2의 거듭제곱 값을 계산하여 더하는 과정이다. 예를 들어, 2진수 '101'을 10진수로 변환하면, 가장 오른쪽 숫자부터 2의 0승, 2의 1승, 2의 2승의 값을 곱해주고, 이를 모두 더한다. 결과적으로 1 * 2의 2승 + 0 * 2의 1승 + 1 * 2의 0승 = 4 + 0 + 1 = 5가 된다.

3) 8진수, 16진수 -> 10진수 변환

8진수와 16진수를 10진수로 변환하는 방법도 2진수와 유사하다. 8진수는 각 자릿수에 8의 거듭제곱을, 16진수는 16의 거듭제곱을 곱한 후 더한다. 16진수의 경우 10 이상의 수는 A(10)부터 F(15)까지 알파벳으로 표현한다.

4) 10진수 -> r진수 (r=2,8,16) 변환

10진수를 다른 진법으로 변환할 때는 나눗셈과 나머지를 활용한다. 예를 들어, 10진수를 2진수로 변환할 때는 2로 계속 나누며 나머지를 기록한다. 이 과정을 몫이 0이 될 때까지 반복하고, 나온 나머지를 역순으로 읽으면 된다.

import java.util.ArrayList;

// 정수 부분 
public class BaseConverter {
    public static void main(String[] args) {
        int decimalNumber = 10; // 입력값: 10진수 정수 부분
        int base = 2; // 변환할 기수 (예: 2진수, 8진수 등)

        ArrayList<Integer> result = convertToBase(decimalNumber, base);

        // 결과 역순으로 출력
        for (int i = result.size() - 1; i >= 0; i--) {
            System.out.print(result.get(i));
        }
    }

    public static ArrayList<Integer> convertToBase(int number, int base) {
        ArrayList<Integer> result = new ArrayList<>();
        int quotient = number / base;
        int remainder = number % base;
        result.add(remainder);

        while (quotient != 0) {
            number = quotient;
            quotient = number / base;
            remainder = number % base;
            result.add(remainder);
        }

        return result;
    }
}

5) 2진수 <-> 8진수, 16진수 변환

2진수와 8진수, 16진수 간의 변환은 비교적 간단하다. 2진수를 8진수로 변환할 때는 2진수의 숫자를 3자리씩 묶어 변환하며, 16진수로 변환할 때는 4자리씩 묶어 변환한다. 반대로 8진수나 16진수를 2진수로 바꿀 때는 각 자리수를 해당하는 2진수로 치환하면 된다.

 

3. 정수 표현

1) 정수 표현 방법

정수를 표현하는 기본적인 방법은 2진수 체계를 활용하는 것이다. 컴퓨터 내부에서는 모든 데이터를 0과 1, 이진 비트의 형태로 표현 -> 정수도 마찬가지.

 

일련의 비트들이 모여 하나의 정수를 나타내게 된다.

2) 부호 없는 정수

• '부호 없는 정수(Unsigned Integer)'는 양의 정수만을 표현하는 방식
• 이 방식에서는 모든 비트가 숫자의 크기를 나타내는 데 사용되며, 특별히 부호를 나타내는 비트는 존재하지 않는다.
• 예를 들어, 8비트 부호 없는 정수는 0부터 255까지의 값을 나타낼 수 있다.

예시: 115와 275의 부호 없는 정수 표현

부호 없는 정수에서는 모든 비트가 숫자의 크기를 결정한다. 예를 들어, 8비트에서 '115'를 표현하려면 2진수로 '01110011'이 된다. 여기서, 가장 왼쪽 비트(최상위 비트)는 0이며, 이는 부호를 나타내지 않는다. 이렇게 해서 115는 0부터 시작하는 8비트 내에서 정확히 표현된다.

 

하지만, 같은 8비트 체계에서 '275'를 표현하려고 하면 문제가 발생한다. 275를 2진수로 변환하면 '100010011'이 되는데, 이는 9비트가 필요하다. 8비트 체계에서는 이를 표현할 수 없으므로, '275'는 오버플로우를 일으키며 정확히 표현할 수 없다.

3) 부호 있는 정수

• '부호 있는 정수(Signed Integer)'는 양의 정수와 음의 정수 모두를 표현할 수 있는 방식이다.
• 이 방식에서는 일반적으로 최상위 비트(MSB)가 부호 비트로 사용되며, 나머지 비트들은 숫자의 크기를 나타낸다.
• 이 부호 비트가 0이면 양수, 1이면 음수를 나타낸다.

• 양의 정수 124의 예시:
  • 2진수로 변환: 124는 2진수로 01111100이다.
  • 여기서 첫 번째 비트(0)는 양수임을 나타내며, 나머지 비트는 124의 값을 나타낸다.
• 음의 정수 -124의 예시:
  • 2의 보수 사용: 음수를 표현하기 위해 2의 보수 방식을 사용한다.
  • 먼저, 124의 2진수 01111100의 모든 비트를 반전시킨다: 10000011.
  • 이제 1을 더한다: 10000100.
  • 결과는 10000100이며, 이는 -124를 나타낸다. 여기서 첫 번째 비트(1)는 음수임을 나타낸다.

4) 8비트 정수 표현 방법의 비교

• 8비트 정수를 예로 들면, 부호 없는 정수는 0부터 255까지를, 부호 있는 정수는 -128부터 127까지를 표현할 수 있다.

5) 2의 보수 방식의 응용

음수의 표현에는 여러 방법이 있으나, 현대 컴퓨터 시스템에서는 주로 '2의 보수(Two's Complement)' 방식을 사용한다.

 

이 방식에서는 음수를 표현하기 위해 숫자의 모든 비트를 반전시킨 후 1을 더한다. 예를 들어, 8비트 2의 보수에서 -1은 11111111로 표현.

 

이 방식은 덧셈과 뺄셈을 간단하게 만들고, 오버플로우 처리를 용이하게 한다.

예시: 24 - 17의 계산

2의 보수 방식을 이용한 계산 예시로 '24 - 17'을 살펴보자. 먼저 24와 17을 8비트 이진수로 표현한다.

• 24(10진수) = 00011000(2진수)
• 17(10진수) = 00010001(2진수)

17을 2의 보수로 변환하여 -17을 만든다. 이를 위해 17의 이진 표현을 먼저 반전시킨 후 1을 더한다.

• 반전: 11101110
• 1 더하기: 11101110 + 1 = 11101111

이제 24와 -17을 더한다.

• 00011000 (24)
• 11101111 (-17)
• 결과: 100001111

8비트로 제한될 경우, 가장 왼쪽의 '1'은 오버플로우로 인해 버려지고, 결과는 '00001111'이 된다. 이는 15를 의미하며, 실제로 24 - 17 = 7이라는 결과와 일치한다.

생각해볼 거리들

• "부호 있는 정수와 부호 없는 정수의 차이를 어떻게 코드로 구현할 수 있을까?"
• "2의 보수 방식을 이용해 음수를 표현하는 과정을 직접 코드로 작성해보면 어떨까?"
• "실제 프로그래밍에서 오버플로우를 방지하기 위해 어떤 점을 주의해야 할까?"
• "다양한 프로그래밍 언어에서 정수 표현 방식이 어떻게 다른지 비교해보면 어떨까?"

4. 실수 표현

1) 실수 표현

컴퓨터 과학에서 실수의 표현은 주로 과학적 표기법을 바탕으로 한 부동소수점 방식을 사용한다. 이 방식은 실수를 가수와 지수로 분리하여 표현하며, 이를 통해 넓은 범위의 실수를 효율적으로 저장할 수 있다.

 

과학적 표기법은 일반적으로 M × 10^E 형태로 표현되며, 여기서 M은 가수, E는 지수.

 

컴퓨터는 이를 이진수 형태로 변환하여 저장한다.

부동소수점의 구성 요소

1. 가수(Mantissa): 실수의 정밀도를 결정한다. 실수의 유효 숫자를 나타내며, 보통 소수점 이하의 숫자들로 구성.
2. 지수(Exponent): 실수의 크기 범위를 결정한다. 가수와 결합하여 실수의 전체 값을 형성.
3. 부호(Sign): 실수가 양수인지 음수인지를 나타내는 부분.

예시: 실수 1,234,000,000,000의 표현

1. 과학적 표기법: 1.234 x 10의 12승
2. 가수와 지수로 분리:
   • 가수: 1.234
   • 지수: 12 (10의 지수 형태)
3. 컴퓨터에서의 표현:
   • 이진수 형태로 변환된 가수와 지수를 사용하여 표현된다.
   • 부호에 따라 가수와 지수의 값이 조정된다.

2) 초과 표기법

초과 표기법은 부동소수점 방식에서 지수 부분을 표현할 때 사용된다. 이 방식은 지수에 '바이어스(bias)'라 불리는 고정된 상수를 더해 저장하는 방법.

 

예를 들어 8비트 지수를 사용하는 시스템에서는 127(2^7-1)이라는 바이어스를 사용하여, 실제 지수 값에 127을 더한 값을 저장한다.

 

이렇게 함으로써 음수와 양수 모두를 효과적으로 표현할 수 있다.

 

3) 정규화

부동소수점 방식에서 실수를 표현할 때는 '정규화' 과정을 거친다. 정규화란 가수 부분이 특정한 형식을 따르도록 만드는 과정이다.

 

일반적으로 가수 부분의 소수점 앞에는 하나의 비트만 1로 설정되고 나머지는 0으로 설정된다.

 

이 과정을 통해 실수를 표준화된 형태로 변환하여, 저장 공간을 효율적으로 사용할 수 있게 한다.

 

4) 실수 표현의 예

예를 들어, 실수 123.456을 부동소수점 방식으로 표현한다면, 먼저 이를 과학적 표기법으로 변환한 뒤, 가수와 지수로 분리한다.

 

이후 지수 부분을 초과 표기법으로 변환하고 가수 부분은 정규화 과정을 거쳐 이진수로 저장한다.

예시: 실수 123.456의 표현 과정

1. 과학적 표기법으로 변환:
   • 먼저, 실수 123.456을 과학적 표기법으로 변환. 이는 1.23456 × 10^2의 형태로 표현. 여기서 1.23456이 가수(mantissa)이고, 10^2가 지수(exponent) 부분.
2. 부동소수점 형식으로 변환:
   • 이제 이 값을 컴퓨터가 이해할 수 있는 부동소수점 형식으로 변환. 이 과정에서 가수와 지수는 이진수 형태로 변환되며, 일반적으로 IEEE 754 표준에 따라 표현.
   • 예를 들어, 단정도 부동소수점 형식에서 32비트 중 가수에 23비트, 지수에 8비트, 부호에 1비트가 할당된다.
3. 이진수 변환:
   • 가수 1.23456을 이진수로 변환하면 약 1.11110111000010100011111이 된다.
   • 지수 2 (10진수)는 이진수로 변환하면 10이 된다.
4. 초과 표기법 적용:
   • 지수 부분은 초과 표기법을 사용하여 저장된다. 예를 들어, 8비트 지수에 127의 바이어스를 더하여 저장. 따라서 10(이진수) + 127 = 137이며, 이진수로는 10001001이 된다.
5. 최종 부동소수점 표현:
   • 최종적으로, 실수 123.456은 부동소수점 형식으로 0 10001001 11110111000010100011111의 이진수로 표현된다. 여기서 처음 0은 양수를 나타내는 부호 비트.

5) IEEE 부동소수점 방식의 표준 형식

IEEE 부동소수점 표준은 실수를 표현하는 데 가장 널리 사용되는 규칙.

 

이 표준은 실수를 저장하는 데 필요한 비트 수(예: 단정도, 배정도)와 가수, 지수의 비트 배치 방식을 정의한다.

 

예를 들어, IEEE 754 표준에 따른 단정도 부동소수점 형식은 총 32비트를 사용하며, 이 중 1비트는 부호, 8비트는 지수, 나머지 23비트는 가수를 나타내는 데 사용된다.

5. 문자 표현

1) 문자 표현

문자를 컴퓨터에서 처리하기 위해선 각 문자에 고유한 코드 값을 할당하는 것이 중요하다.

 

다양한 문자를 일관된 방식으로 처리할 수 있게 함.

2) ASCII 코드

ASCII(American Standard Code for Information Interchange)는 영문 알파벳과 숫자, 특수 문자 등을 포함하는 7비트의 문자 코드.

 

총 128개의 다른 문자를 표현할 수 있으며, 이는 컴퓨터 통신에서 표준적으로 사용된다.

 

ASCII는 각 문자에 대해 0부터 127까지의 숫자를 할당한다.

 

예를 들어, 대문자 'A'는 65, 소문자 'a'는 97의 코드 값을 가진다.

3) 유니코드

유니코드(Unicode)는 전 세계의 모든 문자를 일관된 방식으로 표현하기 위해 만들어진 문자 표준 코드.

 

유니코드는 다양한 언어와 특수 문자를 포함하여 수만 개의 문자를 표현할 수 있다.

 

유니코드는 각 문자에 고유한 코드 포인트를 할당하고, 이를 다양한 방식으로 인코딩할 수 있다.

4) EBCDIC, BCD

EBCDIC(Extended Binary Coded Decimal Interchange Code)는 IBM에서 개발한 8비트 문자 인코딩 체계이며, 주로 IBM의 대형 컴퓨터 시스템에서 사용된다.

BCD(Binary-Coded Decimal)는 각 숫자를 별도의 4비트 이진수로 표현하는 인코딩 방식이다.

 

예를 들어, 숫자 '2'는 0010으로, '9'는 1001로 표현된다.

---

참고자료: 컴퓨터과학개론(이관용, 정광식 공저, KNOU press 출판)